洛谷——图论

1.P1027 Car的旅行路线

题目描述

又到暑假了，住在城市A的Car想和朋友一起去城市B旅游。她知道每个城市都有四个飞机场，分别位于一个矩形的四个顶点上，同一个城市中两个机场之间有一条笔直的高速铁路，第I个城市中高速铁路了的单位里程价格为Ti，任意两个不同城市的机场之间均有航线，所有航线单位里程的价格均为t。

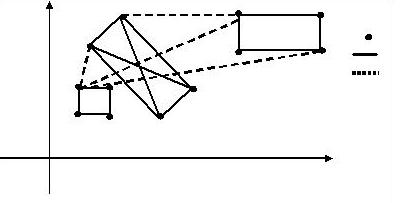
图例（从上而下）

机场 高速铁路

飞机航线

　 注意：图中并没有

标出所有的铁路与航线。

那么Car应如何安排到城市B的路线才能尽可能的节省花费呢?她发现这并不是一个简单的问题，于是她来向你请教。

找出一条从城市A到B的旅游路线，出发和到达城市中的机场可以任意选取，要求总的花费最少。

输入输出格式

输入格式：

第一行为一个正整数n(0<=n<=10)，表示有n组测试数据。

每组的第一行有四个正整数s，t，A，B。

S(0<S<=100)表示城市的个数，t表示飞机单位里程的价格，A，B分别为城市A，B的序号，(1<=A，B<=S)。

接下来有S行，其中第I行均有7个正整数xi1，yi1，xi2，yi2，xi3，yi3，Ti，这当中的(xi1，yi1)，(xi2，yi2)，(xi3，yi3)分别是第I个城市中任意三个机场的坐标，T I为第I个城市高速铁路单位里程的价格。

输出格式：

共有n行，每行一个数据对应测试数据。 保留一位小数

输入输出样例

输入样例#1：

1
3 10 1 3
1 1 1 3 3 1 30
2 5 7 4 5 2 1
8 6 8 8 11 6 3

输出样例#1：

47.5
思路：
　　此题的难点在于求第四个点和记录话费上，至于如何求，运用数学方法（看代码）。。。
　　图论的部分Floyed就可以了。。。
#^_^# 代码：

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;

const int N = 803;
int n,s,t,A,B,xi[N],yi[N],ti[N];
double d[N][N];

void spend(int t1,int t2) {  //求花费 
    d[t1][t2]=sqrt((xi[t1]-xi[t2])*(xi[t1]-xi[t2])+(yi[t1]-yi[t2])*(yi[t1]-yi[t2]));//求图上距离！？ 
    if(((t1-1)/4)==((t2-1)/4)) //判断两点是否在同一个城市中 
        d[t1][t2]=d[t1][t2]*ti[(t1-1)/4+1];//在同一个城市中坐高铁 
    else 
        d[t1][t2]=d[t1][t2]*t;//不在同一个城市中坐飞机 
    d[t2][t1]=d[t1][t2];//从A到B和从B到A距离相同 
    return ;
}

int Find_third(int t1,int t2, int t3) {  //寻找直角三角形直角所在的点，此点的所对点即为第四个点 
    //寻找方法为数学方法，在直角三角形中，斜边最长，不在斜边上的点就为直角所在点 
    if((d[t1][t2]>d[t2][t3])&&(d[t1][t2]>d[t3][t1])) return t3;
    if((d[t3][t1]>d[t1][t2])&&(d[t3][t1]>d[t2][t3])) return t2;
    if((d[t2][t3]>d[t3][t1])&&(d[t2][t3]>d[t1][t2])) return t1;
}

void Calc_third(int t1,int t2,int t3) {
    spend(t1,t2); //计算出花费，找第四条边 
    spend(t3,t1);
    spend(t2,t3);
    int Third=Find_third(t1,t2,t3);
    if(Third==t1){ 
        xi[t3+1]=xi[t3]+xi[t2]-xi[t1];
        yi[t3+1]=yi[t3]+yi[t2]-yi[t1];
    }
    else if(Third==t2) {
        xi[t3+1]=xi[t3]+xi[t1]-xi[t2];
        yi[t3+1]=yi[t3]+yi[t1]-yi[t2];
    }
    else if(Third==t3) {
        xi[t3+1]=xi[t1]+xi[t2]-xi[t3];
        yi[t3+1]=yi[t1]+yi[t2]-yi[t3];
    }
}

int main() {
    cin>>n;
    for(int i=1; i<=n; i++)
    {
        cin>>s>>t>>A>>B;
        for(int i=1; i<=401; i++) //初始化 
            for(int j=1; j<=401; j++) 
                d[i][j]=0x7fffffff;
        for(int i=1; i<=s; i++) {
            cin>>xi[i*4-3]>>yi[i*4-3]>>xi[i*4-2]>>yi[i*4-2]>>xi[i*4-1]>>yi[i*4-1]>>ti[i]; //为什么要i*4-3，i*4-2，i*4-1呢？？
            //小技巧，前三条边的坐标依次存输入在数组中，将第四个位置空下，等后来存放第四条边的坐标 
            Calc_third(i*4-3,i*4-2,i*4-1); //寻找第四条边 
        }
        for(int i=1; i<=4*s; i++) //将所有边都找完以后，重新计算花费记录下来，寻找答案 
            for(int j=1; j<=4*s; j++) 
                spend(i,j);
        for(int k=1; k<=4*s; k++) //Floyed 
            for(int i=1; i<=4*s; i++)
                for(int j=1; j<=4*s; j++)
                    if(d[i][k]+d[k][j]<d[i][j])
                        d[i][j]=d[i][k]+d[k][j];
        double ans=3456789.0;
        for(int i=4*A-3; i<=4*A; i++)
            for(int j=4*B-3; j<=4*B; j++) 
                if(ans>d[i][j]) //找最小值 
                    ans=d[i][j];
        printf("%.1lf\n",ans);
    }
    return 0;
}

2.P1629 邮递员送信

题目描述

有一个邮递员要送东西，邮局在节点1.他总共要送N-1样东西，其目的地分别是2~N。由于这个城市的交通比较繁忙，因此所有的道路都是单行的，共有M条道路，通过每条道路需要一定的时间。这个邮递员每次只能带一样东西。求送完这N-1样东西并且最终回到邮局最少需要多少时间。

输入输出格式

输入格式：

第一行包括两个整数N和M。

第2到第M+1行，每行三个数字U、V、W，表示从A到B有一条需要W时间的道路。 满足1<=U,V<=N,1<=W<=10000,输入保证任意两点都能互相到达。

【数据规模】

对于30%的数据，有1≤N≤200;

对于100%的数据，有1≤N≤1000,1≤M≤100000。

输出格式：

输出仅一行，包含一个整数，为最少需要的时间。

输入输出样例

输入样例#1：

5 10
2 3 5
1 5 5
3 5 6
1 2 8
1 3 8
5 3 4
4 1 8
4 5 3
3 5 6
5 4 2

输出样例#1：

83
思路：
　　因为邮递员送和回都要计算，所以跑两遍SPFA，而且一次只能拿一件，所以答案就是从邮局到所有点的最短路的和，（累加）。
　　注意边数组一定要开大！！！

#^_^# 代码：

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;

queue<int>q;
const int N=1003;
const int M=100003;
struct Edge{
    int pre; int to; int w;
}edge[M*4];
int u[M],v[M],w[M];

struct edge{
    int to;int l;
}dl[N][N];

int n,m,num_edge,head[M],vis[M],dis[M],sum;

void build(int u,int v,int w) {
    edge[++num_edge].pre = head[u];
    edge[num_edge].to = v;
    edge[num_edge].w = w;
    head[u] = num_edge;
}

void SPFA() {
    while(!q.empty()) q.pop();
    memset(dis,0x7f,sizeof(dis));
    memset(vis,0,sizeof(vis));
    vis[1]=1;
    dis[1]=0;
    q.push(1);
    while(!q.empty()) {
        int s=q.front();
        q.pop();
        vis[s]=0;
        for(int i=head[s]; i; i=edge[i].pre) {
            int to=edge[i].to;
            if(dis[s]+edge[i].w<dis[to]) {
                dis[to]=dis[s]+edge[i].w;
                if(!vis[to]) {
                    vis[to]=1;
                    q.push(to); 
                }
            }
        }
    }
    for(int i=2; i<=n; i++) 
       sum+=dis[i];
}

int main() {
    scanf("%d%d",&n,&m);
    for(int i=1; i<=m; i++) {
        scanf("%d%d%d",&u[i],&v[i],&w[i]);
        build(u[i],v[i],w[i]);
    }
    SPFA();
    memset(edge,0,sizeof(edge));
    memset(head,0,sizeof(head));
    for(int i=1; i<=m; i++) {
        build(v[i],u[i],w[i]);
    }
    SPFA();
    cout<<sum<<endl;
    return 0;
}

自己选的路，跪着也要走完！！！