51nod-3986-免费的馅饼

https://class.51nod.com/Html/Textbook/Problem.html#problemId=3986&textbookChapterId=725

https://class.51nod.com/Html/Textbook/ChapterIndex.html#textbookId=126&chapterId=338

我们将馅饼表示为 \((p_i,t_i)\)，即一个平面直角坐标系上的点。

我们把馅饼看成静止，人每次往上移动一格。

记当前点为 \((x_0,y_0)\)，考虑能转移到当前点的馅饼满足的条件。

向上走的路程为 \(y_0-y\)，左右为 \(x_0-x\)。

一直往右：\(2(y_0-y)=x_0-x\)。

一直往左：\(-2(y_0-y)=x_0-x\)。（此时两边都是负值）

由于每次只能最多走2格，所以 \(2(y_0-y)\ge x_0-x\)，得 \(x-2y\ge x_0-2y_0\)，变为 \(2y-x\le 2y_0-x_0\)。

同理，\(-2(y_0-y)\le x_0-x\)。（即左边的绝对值更大），得 \(x+2y\le x_0+2y_0\)。

单独满足一个条件不满足 \(y<y_0\)，但是同时满足就同时满足这一条件，如图：

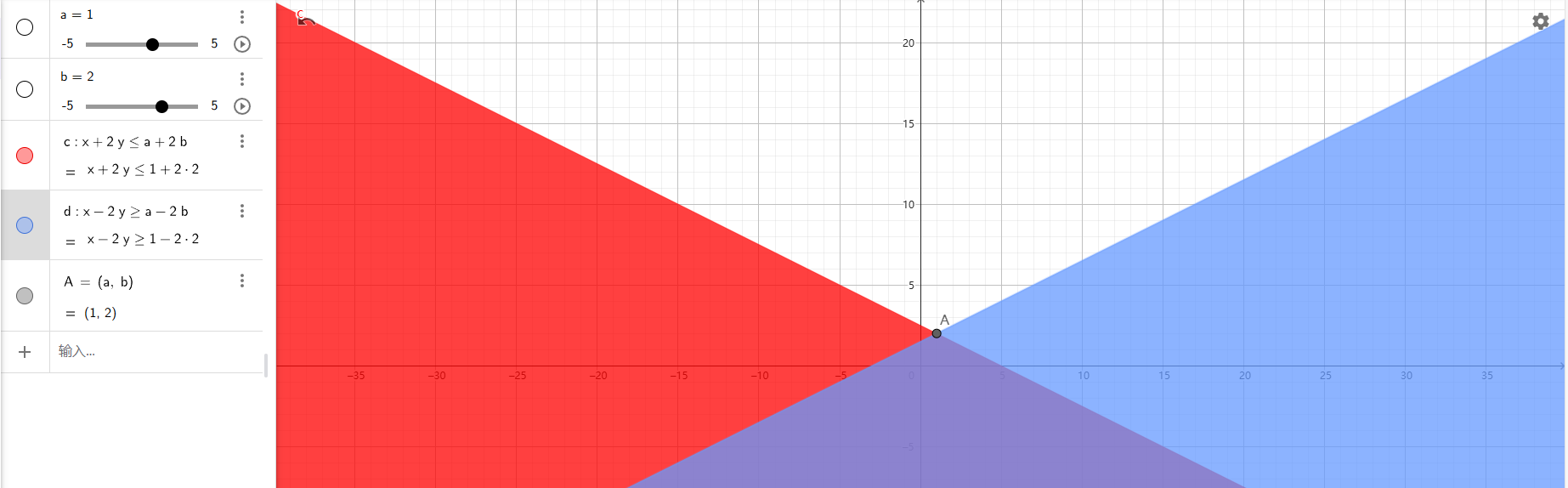
动态：https://www.geogebra.org/m/zv9vwhzk

即紫色区域。

至此，令 \(x'=2y-x,y'=x+2y\)，此时变成了一个二维偏序问题，只要满足 \(x'\le x_0',y'\le y_0'\) 的就可以转移。

通过排序去掉一维，另一维树状数组维护之。

当然要离散化树状数组那一维。

\(O(n\log n)\)。

#include<iostream>
#include<algorithm>
using namespace std;
const int N=100010;
int w,n,ls[N],f[N];
struct bing{
	int x,y,v,lv,rv;
	void init(){
		cin>>y>>x>>v;
		lv=y*2-x;
		rv=x+y*2;
	}
	bool operator<(const bing&B)const{
		// return rv<B.rv;
		return rv^B.rv?rv<B.rv:lv<B.lv;
	}
}b[N];
int c[N];
void add(int x,int v){
	for(;x<=n;x+=x&-x)c[x]=max(c[x],v);
}
int sum(int x){
	int res=0;
	for(;x;x-=x&-x)res=max(res,c[x]);
	return res;
}
int main(){
	#ifdef LOCAL
	freopen("1.txt","r",stdin);
	#endif
	#ifndef LOCAL
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	#endif
	cin>>w>>n;
	for(int i=1;i<=n;++i)b[i].init(),ls[i]=b[i].lv;
	sort(b+1,b+1+n);
	// for(int i=1;i<=n;++i)
		// cout<<b[i].rv<<' '<<b[i].lv<<' '<<b[i].v<<'\n';
	sort(ls+1,ls+1+n);
	int m=unique(ls+1,ls+1+n)-ls-1;
	for(int i=1;i<=n;++i)
		b[i].lv=lower_bound(ls+1,ls+1+m,b[i].lv)-ls;
	int ans=0;
	for(int i=1;i<=n;++i){
		f[i]=sum(b[i].lv)+b[i].v;
		ans=max(ans,f[i]);
		add(b[i].lv,f[i]);
	}
	cout<<ans;
	return 0;
}