acwing351
https://www.acwing.com/activity/content/problem/content/9051/
NOIP2007提高组T4。本题是加强版。
题目描述
设 \(T=(V, E, W)\) 是一个无圈且连通的无向图（也称为无根树），每条边带有正整数的权，我们称 \(T\) 为树网（treenetwork），其中 \(V, E\) 分别表示结点与边的集合，\(W\) 表示各边长度的集合，并设 \(T\) 有 \(n\) 个结点。
路径：树网中任何两结点 \(a,b\) 都存在唯一的一条简单路径，用 \(d(a,b)\) 表示以 \(a,b\) 为端点的路径的长度，它是该路径上各边长度之和。
我们称 \(d(a,b)\) 为 \(a,b\) 两结点间的距离。
一点 \(v\) 到一条路径 \(P\) 的距离为该点与 \(P\) 上的最近的结点的距离：
\(d(v，P)=min\{d(v，u)\}\)，\(u\) 为路径 \(P\) 上的结点。
树网的直径：树网中最长的路径称为树网的直径。
对于给定的树网 \(T\)，直径不一定是唯一的，但可以证明：各直径的中点（不一定恰好是某个结点，可能在某条边的内部）是唯一的，我们称该点为树网的中心。
偏心距 \(ECC(F)\)：树网 \(T\) 中距路径 \(F\) 最远的结点到路径 \(F\) 的距离，即：
\(ECC(F)=max\{d(v,F),v∈V\}\)
任务：对于给定的树网 \(T=(V, E,W)\) 和非负整数 \(s\)，求一个路径 \(F\)，它是某直径上的一段路径（该路径两端均为树网中的结点），其长度不超过 \(s\)（可以等于 \(s\)），使偏心距 \(ECC(F)\) 最小。
我们称这个路径为树网 \(T=(V,E,W)\) 的核（Core）。
必要时，\(F\) 可以退化为某个结点。
一般来说，在上述定义下，核不一定只有一个，但最小偏心距是唯一的。
输入格式
包含 \(n\) 行： 第 \(1\) 行，两个正整数 \(n\) 和 \(s\)，中间用一个空格隔开，其中 \(n\) 为树网结点的个数，\(s\) 为树网的核的长度的上界，设结点编号依次为 \(1, 2, …, n\)。
从第 \(2\) 行到第 \(n\) 行，每行给出 \(3\) 个用空格隔开的正整数，依次表示每一条边的两个端点编号和长度。
例如，2 4 7 表示连接结点 \(2\) 与 \(4\) 的边的长度为 \(7\)。
所给的数据都是正确的，不必检验。
输出格式
只有一个非负整数，为指定意义下的最小偏心距。
数据范围
\(1 \le n \le 500000\)
\(0 \le s \lt 2^{31}\)
\(0 \le 树的直径长度 \lt 2^{31}\)
输入样例：
5 2
1 2 5
2 3 2
2 4 4
2 5 3
输出样例：
5
算法
(暴力) \(O(n^2(n^2\log n))\)
直接枚举每一条直径，然后用双指针算法找到左端点确定右边尽可能长的路径，然后根据定义计算（用 \(n\) 个优先队列维护每个点到路径上的点的最小值）。
原题就可以得到93分（一个测试点被菊花图卡了）。（一般情况下复杂度 \(O(n^2\log n)\)）
正解
Part 1.计算1条直径就够的分析
对于给定的树网 \(T\)，直径不一定是唯一的，但可以证明：各直径的中点（不一定恰好是某个结点，可能在某条边的内部）是唯一的，我们称该点为树网的中心。
据此猜测我们只需要计算一条直径就可得到答案。
挖掘性质：
性质1，1棵树中，任意两条直径都是相交的
假设两条直径不相交，一定存在某条简单路径将两条直径连起来。形如此：
选择其中最长的两条分链加上用于连接的简单路径，会得到一条更长的直径，与假设矛盾。
而且重叠肯定只有连续的一段，不然就形成环了。
性质2，各条直径在不相交的两端，长度分别相等
考虑两条直径AB和CD，它们的重叠部分为EF。
直径最长，新的组合长度不能超过直径长度。因此(DF = BF,AE = EC)。
性质3，计算一条直径就可以得到答案
证明我们只取公共部分EF中的点可以得到最优解即可（因为这样对于每条直径都是等价的）
情况1：
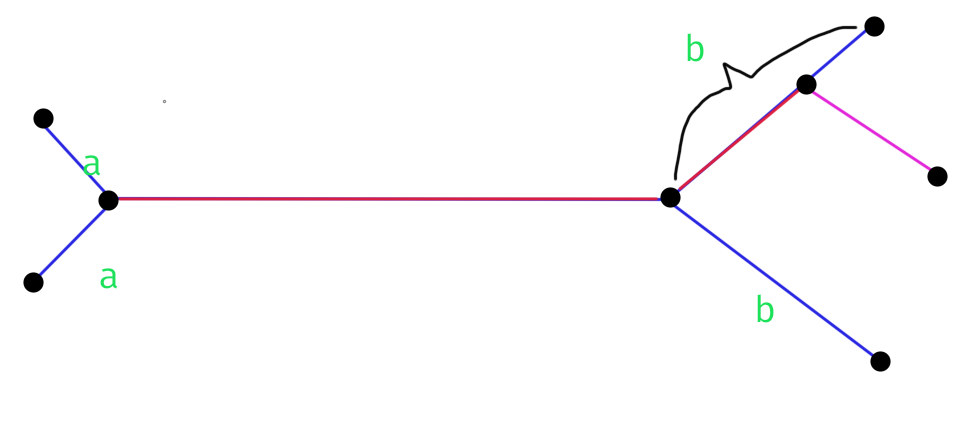
红色表示选择的部分，紫色表示优化使得答案更小的。
由于是直径，所以紫色+红色<=b，因此我们优化的距离是一个本来就<=b的，而最大值至少是b，所以可以删去。
情况2、3：
同理，图放在这里按照上面的方法推测。
同理可知，对于另一条b成立。
同理可知，对于a也成立。
第一条直径和第二条直径只需要计算第一条直径，第一条直径和第三条直径只需要计算第一条直径……
所以我们只需要计算一条直径。
Part 2.
把一条直径抠出来，还是要用到上面暴力中的做法，找到 \(L,R\).
考虑答案分为三部分：
- L到左边直径的部分（其他分支不会更大了，跟Part 1类似）
- R到右边直径的部分
- 中间的点到其对应分支的部分（记为集合 \(A\)）
预处理出直径上的点到它挂的子树最深的点。
此时发现可以用单调队列维护中间部分距离最远的点，两边的用前缀和。
复杂度已经达到 \(O(n)\)。
Part 3.
继续优化。
考虑答案中1、2部分，可以把其他每个点（记为集合 \(B\)）挂下去的分支统计进去，不会影响结果。（因为距离必然<=L到左边直径的部分或R到右边直径的部分）
这样我们只要求1、2部分，然后合并 \(A,B\)，得到需要求解的是整条直径上每个点挂下去的深度最大值的最大值即可。
单调队列也省去了，只需要前缀和
时间复杂度
\(O(n)\)
空间复杂度
\(O(n)\)
C++ 代码
#include<bits/stdc++.h>
using namespace std;
const int N=500010,M=2*N;
int n,s,h[N],e[M],ne[M],w[M],fa[N],dep[N],q[N],sum[N],idx;
bool st[N];
void add(int a,int b,int c){
w[idx]=c,e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int dfs(int x,int f){
int res=x;
fa[x]=f;
// printf("%d:dep=%d,fa=%d\n",x,dep[x],fa[x]);
for(int i=h[x];~i;i=ne[i]){
int j=e[i];
if(j==f||st[j])continue;
dep[j]=dep[x]+w[i];
int k=dfs(j,x);
if(dep[k]>dep[res])res=k;
}
// printf("%d:res=%d\n",x,res);
return res;
}
int work(){
int xx=dfs(1,0);
// return 0;
dep[xx]=0;
int y=dfs(xx,0);
int cnt=0,ans=INT_MAX;
for(;y;y=fa[y]){
q[cnt++]=y;
sum[cnt]=sum[cnt-1]+dep[y]-dep[fa[y]];
st[y]=1;
}
int t1=0;
for(int i=0;i<cnt;++i)
dep[q[i]]=0,t1=max(t1,dep[dfs(q[i],0)]);
for(int i=0,j=0;i<cnt;++i){
while(j<cnt&&sum[j+1]-sum[i]<=s)++j;
int t2=sum[i],t3=sum[cnt-1]-sum[j];
ans=min(ans,max(t1,max(t2,t3)));
}
return ans;
}
int main(){
#ifndef ONLINE_JUDGE
freopen("1.txt","r",stdin);
#endif
#ifdef ONLINE_JUDGE
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
#endif
cin>>n>>s;
memset(h,-1,n*4+4);
for(int i=1;i<n;++i){
int a,b,c;
cin>>a>>b>>c;
add(a,b,c),add(b,a,c);
}
cout<<work();
return 0;
}
本题重点就是分析。
