联合权值

P1351 [NOIP2014 提高组] 联合权值

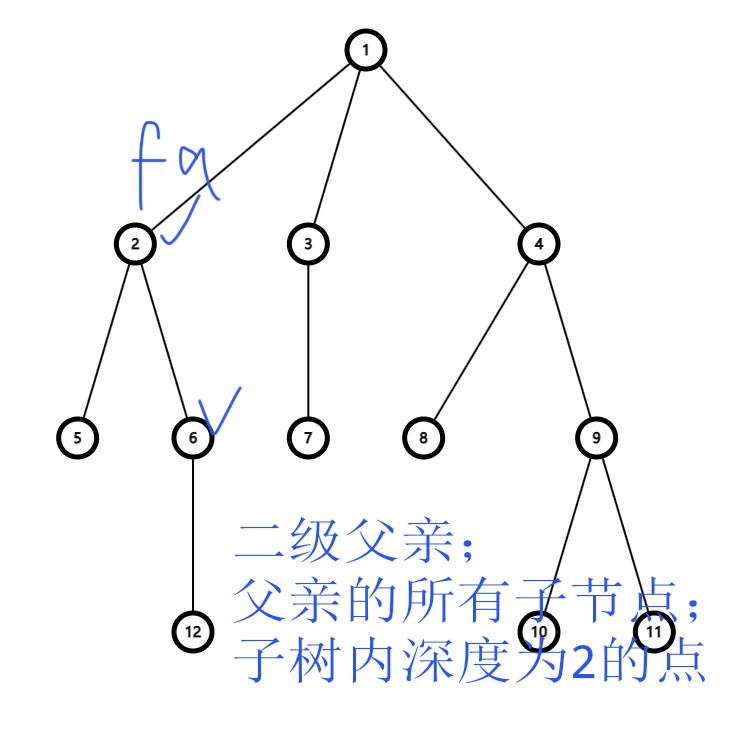
我们对于每个点计算它的子结点的 \(\sum w,\max w\)。

如图，发现贡献有三类：

1. 直接计算。
2. 需要剔除自己这个点，对于 sum 直接减去即可，对于 max 维护一个次大值，发现这个点是最大值用次大值代替。
3. 枚举子节点，然后直接利用子节点的 \(\sum,\max\) 信息。

复杂度线性。

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
#define Ed for(int i=h[x];~i;i=ne[i])
#define Ls(i,l,r) for(int i=l;i<r;++i)
#define Rs(i,l,r) for(int i=l;i>r;--i)
#define Le(i,l,r) for(int i=l;i<=r;++i)
#define Re(i,l,r) for(int i=l;i>=r;--i)
#define L(i,l) for(int i=0;i<l;++i)
#define E(i,l) for(int i=1;i<=l;++i)
#define W(t) while(t--)
#define Wh while

const int N=200010,M=2*N,mod=10007;
int n,w[N],mx[N],cm[N],f[N],ans_max,sum[N],ans_sum;
typedef long long ll;
int h[N],e[M],ne[M],idx;//don't forget memset h!
void add(int a,int b){
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
#define pls(a,b) (a+=b)>=mod&&(a-=mod)

void init(int x,int fa){
    f[x]=fa;
    Ed{
        int j=e[i];
        if(j==fa)continue;
        int var=w[j];
        pls(sum[x],var);
        if(var>=w[mx[x]])cm[x]=mx[x],mx[x]=j;
        else if(var>w[cm[x]])cm[x]=j;
        init(j,x);
    }
}
int max(int a,int b){
    // cout<<b<<'+';
    return a>b?a:b;
}
void dfs(int x){
    int gpa=f[f[x]];
    if(~gpa)
        pls(ans_sum,w[gpa]*w[x]%mod),
        ans_max=max(ans_max,w[gpa]*w[x]);
    int fa=f[x];
    if(~fa)pls(ans_sum,(sum[fa]-w[x]+mod)*w[x]%mod);
    ans_max=max(w[mx[fa]==x?cm[fa]:mx[fa]]*w[x],ans_max);
    Ed{
        int j=e[i];
        if(j==fa)continue;
        pls(ans_sum,sum[j]*w[x]%mod);
        ans_max=max(ans_max,w[mx[j]]*w[x]);
        dfs(j);
    }
}
int main(){
    #ifndef ONLINE_JUDGE
    freopen("1.in","r",stdin);
    #endif
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin>>n;
    memset(h,-1,n*4+4);
    E(i, n-1){
        int a,b;
        cin>>a>>b;
        add(a,b),add(b,a);
    }
    E(i, n)cin>>w[i];
    init(1,-1);
    // E(i, n)cout<<sum[i]<<' '<<mx[i]<<' '<<cm[i]<<'\n';
    dfs(1);
    cout<<ans_max<<' '<<ans_sum<<'\n';
    return 0;
}