tarjan(dcc-e)

冗余路径

考虑无向图的边双连通分量。

这个算法也叫 Tarjan 算法，且与有向图的强连通分量差不多。

边双是指图中任意两点间都存在两条不相交的路径（或删去任意一条边后图仍然连通）。

桥：切去这条边后，图不连通。

由于这是无向图，所以定义中不包含横叉边。

考虑依然维护 dfn 和 low。

区别在于，如果是第一次遍历同有向图，同样用low更新low。如果是第二次，只需判断是不是这条边是不是父亲边的反向边，而不需要判断是不是在栈中。同时无需标记某个点是否在栈中。

void tarjan(int x,int from){
    dfn[x]=low[x]=++now;
    stk[++top]=x;
    Ed{
        int j=e[i];
        if(!dfn[j]){
            tarjan(j,i);
            low[x]=min(low[x],low[j]);
            if(dfn[x]<low[j])b[i]=b[i^1]=1;
        }
        else if(i!=(from^1))low[x]=min(low[x],dfn[j]);
    }
    if(low[x]==dfn[x]){
        ++dcc_cnt;
        int y;
        do{
            y=stk[top--];
            id[y]=dcc_cnt;
        }while(y!=x);
    }
}

这道例题，我们首先缩点，因为在一个dcc-e中的所有点一定满足要求。而缩点结束后所有的边都是桥，所以就是一棵树，相当于在树上加边使其变为边双连通分量，一个比较好想的就是所有度为1的点首尾相接，形成环，若剩余一点随便搞，如下图。

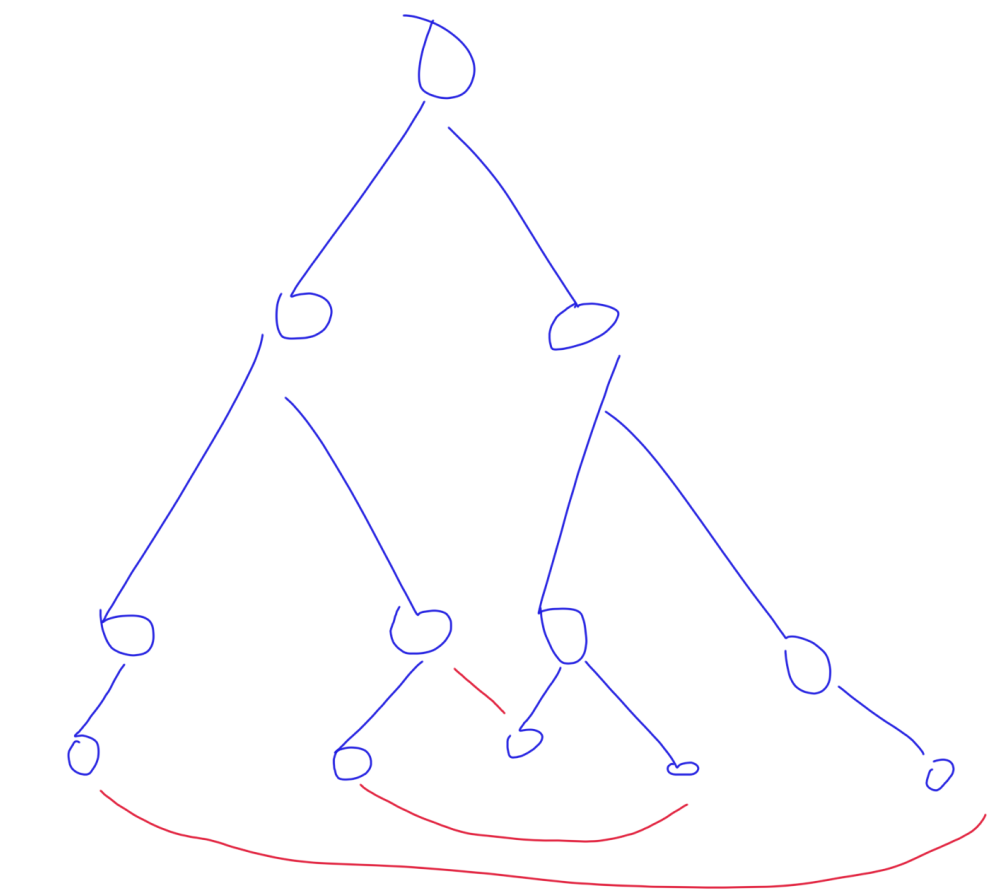
最少需要的边数恰好是度为1的点数除以2上取整，即度为1的点数加1下取整。

code

点双太麻烦，给出割点的判定：
对于 \(u,v\)，\(dfn[u]\le low[v]\)。