TripleIndex
[ABC293G] Triple Index
借本题来描述一下莫队算法。
莫队算法是将询问离线排序，使得时间复杂度控制在 \(n\sqrt n\) 的量级。
首先考虑暴力做法，每次对于一个询问，将询问中的区间内的数依次加入桶中，第一次出现答案增加一，询问完清空，复杂度 \(O(qn)\)。
考虑一个稍快的做法，将所有询问按照右端点排序，并且利用上次右端点的信息，这样右端点的移动次数可以控制在 \(O(n)\)，但左端点最坏情况依然是 \(O(n^2)\)。
我们可以考虑将原数组分成 \(\sqrt n\) 块，然后对所有询问先按照左端点所在的块排序，若同块中则按照右端点从小到大排序①，然后再执行，可以发现右端点在同块中恰好是从左移到右（当然需要从上次末尾的位置移到开头，2倍常数），所以共 \(n\sqrt n\) 次，左端点移动 \(q\) 次，每次在块内移动距离 \(\le \sqrt n\)，跨块一次最多 \(2\sqrt n\)，最多跨块 \(\sqrt n\) 次，所以左端点移动 \(q\sqrt n+2n\)，单次移动 \(O(1)\) 修改，复杂度 \(O(n\sqrt n+q\sqrt n)\)。
实际上，设块长为 \(A\)，共 \(n/A\) 块，则右端点次数 \(n^2/A\)，左端点 \(qA\)，令 \(n^2/A=qA\)，所以当块长取到 \(\sqrt{n^2/q}\) 时最优。
还有一个对①的常数优化，就是根据块的奇偶性排序，如果是奇数按照右端点从小到大，否则从大到小，这个道理很简单，如图
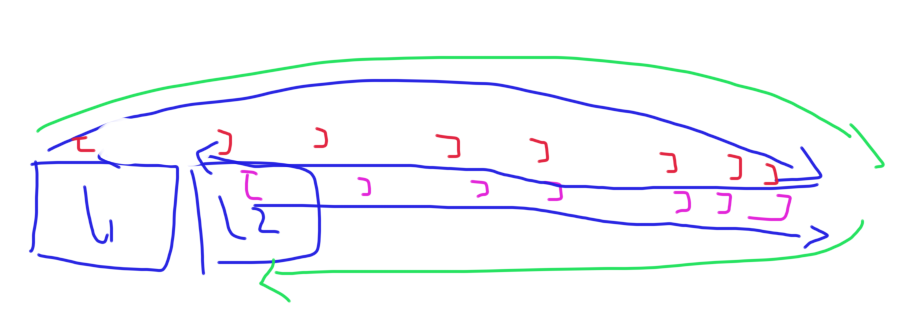
对于不优化，那么右端点的行动路线如蓝色轨迹，优化后如绿色轨迹。（这样对于右端点的优化，可以使其少走一半的路径）
考虑此题，我们其实只需要记录每个数出现了多少次就够了。
每次增加一个数，设原来的个数为 \(x\)，实际上答案会增加 \(C_{x+1}^3-C_{x}^3\)，即增加 \(\dfrac{x(x-1)}{2}\)。
每次减少一个数，设修改后的的个数为 \(x\)，实际上答案会减少 \(C_{x+1}^3-C_{x}^3\)，即减少 \(\dfrac{x(x-1)}{2}\)。
复杂度 \(O(\sqrt{n^2/q}\times q)=O(\sqrt{n^2q})=O(n\sqrt q)\)。
