YetAnotherGridTask

[ABC311F] Yet Another Grid Task

考虑找规律。

我们先将必定要填黑的格子填完。

对于以下的矩形

....#.
......
.#....
......
......

处理后

....#.
....##
.#..##
.##.##
.#####

一个必要的观察是：对于从右上角到左下角的次对角线，对角线上必定存在一个分界点，使得其左边全为白，其右边包括其在内全为黑，且随着对角线的移动，分界点往左。

具体的图

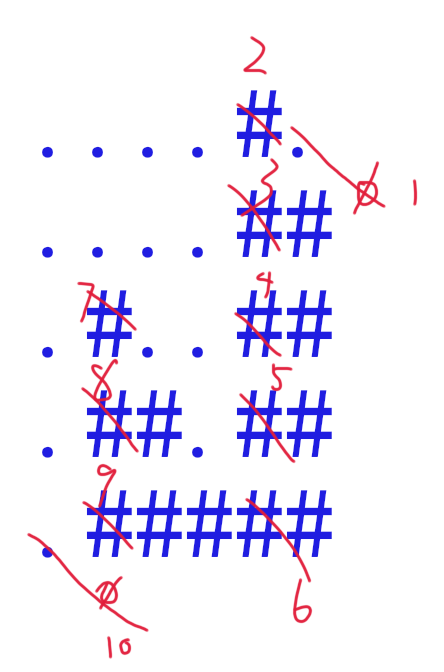
空的话就当作最后一个白色的右边。

如上图 $1\sim 10$ 分别表示位置，可以发现非严格的向左移动。

根据这个性质我们可以 DP，较容易的设计状态并转移。

令 $f[c][j]$ 表示在 $i-j=c$ 的副对角线上，$(j+c,j)$ 点及其往右的格子均涂黑的答案。

我们从右上往左下 DP。

为了方便起见，我们假设网格在右方向和下方向上是无限大的，并且下面/右面增加的无限格子均为黑色。

然后令 $f[-m][m+1]=1,f[-m][j]=0(1\le j\le m)$。

• 首先，可以得到方程 $f[c][j]=\sum _{k=j}^{m+1}f[c-1][k]$（$m+1$ 即全白，我们忽略越界）。
• 其次，若 $i=j+c<0,f[c][j]=0$。
• 最后，如果 $(i=j+c,j)$ 这个格子必须为黑色（包括 $i>=n$，因为我们规定了网格在右方向和下方向上是无限大的），那么 $f[c][j+1]=0$（因为 $(j+c,j)$ 这个格子必定被染）。

答案就是 $\sum _{j=1}^{m+1}f[n-1][j]$。

复杂度 $O(nm)$。

AC

另外一种理解方式

如果将题目变更为下方、右方，那么令 $f[i][j]$ 表示前 $i$ 行已经成为美丽网格的情况下，第 $i$ 行的涂格子情况为 $(i,j)$ 右侧的格子均涂黑。

转移显然，$f[i][j]=\sum _{k\ge j}f[i-1][k]$。

然后如果我们对原网格进行变形，将它拉成一个平行四边形，即将给定的网格向下推，使其左上角斜向变形如下：

#...#
.....
.....
.....
#....

  ↓

    #
   ..
  ...
 ....
#....
....
...
..
#

这样做的话，“下和右下”这个条件就变成了“下和右”的条件，因此可以像前面提到的问题一样解决。

这个做法其实和对角线的做法如出一辙。