[NOI2014]动物园

[NOI2014] 动物园

这题看题目描述就知道一定是跟 KMP 扯上关系了。首先，如果不考虑长度超过 \(\dfrac{1}{2}\) 的限制的话，那么就很简单，每次求出一个新的 \(ne_i\) 时，如下图所示

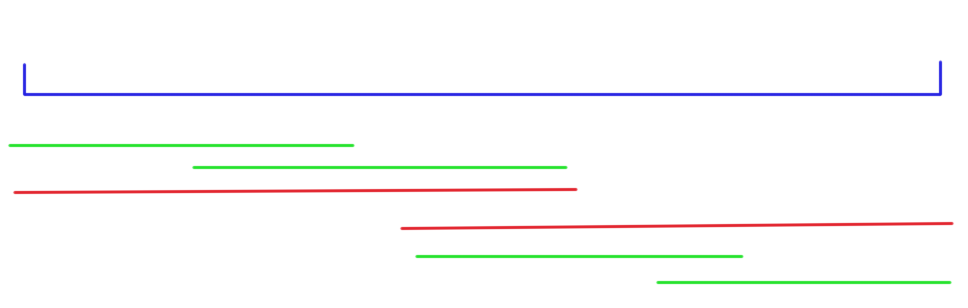
图中红色的表示目前对于前 \(i\) 个字符来说，最长公共前后缀为红色部分，因为两个红色部分中一定都有前后缀（即绿色部分），所以最左侧的绿色串和最右侧的是相等的。也就是说，对于 \(i\) 可以继承它的最长公共前后缀 \(ne[j]\) 的所有答案。所以如果 \(ne_i=j\)，则个数 \(cnt_i=cnt_j+1\)。

现在我们并没有考虑限制，那应该怎么办呢？可以在做的时候先从 \(ne_i\) 开始往前跳，跳到第一个满足要求为止。但这样显然是可以被卡成 \(O(N^2)\)，不过可以得 \(50\) 分。

#include<cstdio>
#include<cstring>
using namespace std;
#define Ls(i,l,r) for(int i=l;i<r;++i)
#define Rs(i,l,r) for(int i=l;i>r;--i)
#define Le(i,l,r) for(int i=l;i<=r;++i)
#define Re(i,l,r) for(int i=l;i>=r;--i)
#define L(i,l) for(int i=0;i<l;++i)
#define E(i,l) for(int i=1;i<=l;++i)
#define W(t) while(t--)
const int N=1000010,mod=1e9+7;
int T,n,ne[N],num[N],ans;
char s[N];
int main(){
	#ifndef ONLINE_JUDGE
	freopen("1.in","r",stdin);
	// freopen("1.out","w",stdout);
	// ios::sync_with_stdio(0);
	// cin.tie(0);
	// cout.tie(0);
	#endif
	// Insert Code Here
	scanf("%d",&T);
	while(T--){
		scanf("%s",s+1);
		n=strlen(s+1);
		int j=0;
		num[1]=1;
		for(int i=2;i<=n;++i){
			while(s[j+1]!=s[i]&&j)j=ne[j];
			if(s[j+1]==s[i])++j;
			ne[i]=j;
			num[i]=num[j]+1;
		}
		long long ans=1;
		for(int i=1;i<=n;++i){
			int j=ne[i];
			while(j*2>i)j=ne[j];
			ans=ans*(num[j]+1)%mod;
		}
		printf("%lld\n",ans);
	}
	return 0;
}

接下来考虑优化。这样跳是有很多冗余的状态的，我们可以想到并查集路径压缩的思想，但只能是一个类路径压缩的做法。我们再做一遍 KMP，使用之前求得的 ne 数组进行跳跃，由于每次 \(j\) 最多增大 \(1\)，所以本来 \(38\) 行的 while 语句最多执行一次，即可以改成 if，这样就是两遍 KMP 的复杂度。但这样求得的答案会不会不是最优的呢？显然是不会的，因为你往后扩张了 \(1\)，那么它先判断的肯定是最长的，反正肯定是对的。这个东西看代码就懂了。

#include<cstdio>
#include<cstring>
using namespace std;
#define Ls(i,l,r) for(int i=l;i<r;++i)
#define Rs(i,l,r) for(int i=l;i>r;--i)
#define Le(i,l,r) for(int i=l;i<=r;++i)
#define Re(i,l,r) for(int i=l;i>=r;--i)
#define L(i,l) for(int i=0;i<l;++i)
#define E(i,l) for(int i=1;i<=l;++i)
#define W(t) while(t--)
const int N=1000010,mod=1e9+7;
int T,n,ne[N],num[N],ans;
char s[N];
int main(){
	#ifndef ONLINE_JUDGE
	freopen("1.in","r",stdin);
	// freopen("1.out","w",stdout);
	// ios::sync_with_stdio(0);
	// cin.tie(0);
	// cout.tie(0);
	#endif
	// Insert Code Here
	scanf("%d",&T);
	while(T--){
		scanf("%s",s+1);
		n=strlen(s+1);
		int j=0;
		num[1]=1;
		for(int i=2;i<=n;++i){
			while(s[j+1]!=s[i]&&j)j=ne[j];
			if(s[j+1]==s[i])++j;
			ne[i]=j;
			num[i]=num[j]+1;
		}
		int ans=1;
		j=0;
		for(int i=1;i<=n;++i){
			while(j&&s[j+1]!=s[i])j=ne[j];
			if(s[j+1]==s[i])++j;
			if(j*2>i)j=ne[j];
			ans=ans*(num[j]+1ll)%mod;
		}
		printf("%lld\n",ans);
	}
	return 0;
}