假期计划

假期计划

由于要考虑相邻城市之间的中转点不超过 $k$（即所经过边数不超过 $k+1$），所以首先要预处理出 $dis[i][j]$，即两两之间的点的距离，可以 bfs $n$ 次解决。然后就是考虑怎么进行枚举了。首先如果直接枚举四个点显然不可行，时间复杂度是 $O(n^4)$，应该想到一个技巧：折半枚举。假设点依次是 $1->A->B->C->D->1$，可以先考虑弄 $1->A->B$，再弄 $1->C->D$，然后想办法拼接起来。

接下来是重点：对于每个点，都记录一个从 $1$ 到某个中间点再到它的贡献，然后取贡献前三名的中间点。然后枚举 $B，D$ 两点，取它们存储的中转点 $A,C$ 进行两两组合，应该有 $3\times 3=9$ 种情况。

这个做法的确很好，但为什么取贡献前三名的点呢？

假如留一个，万一 $B,D$ 的 $A,C$ 相等，显然不合法。

假如留两个，如下图

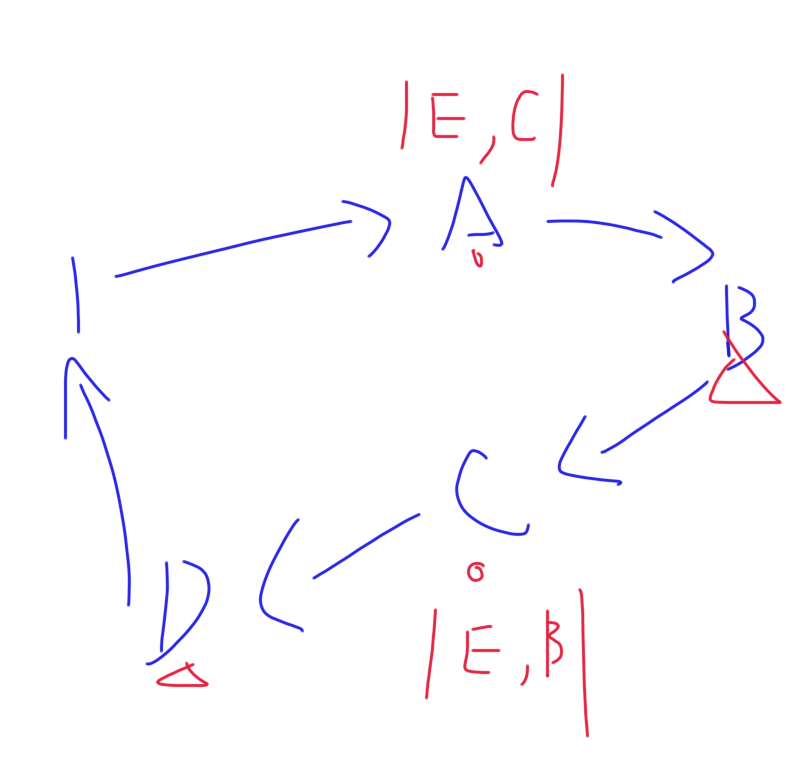
上图中，无论 $A,C$ 怎么组合，都会只有 $2\sim 3$ 个不同的点。

留三个，如下图

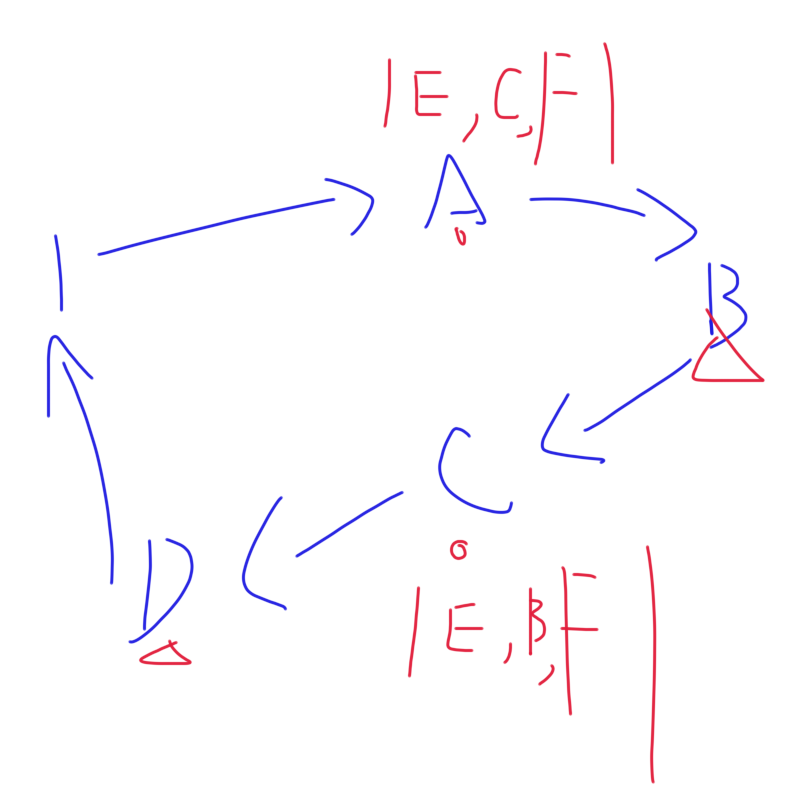
就算有 $B,C$，其他的都相同，也可以构造出 $1->E->B->F->D->1$。上述的是最坏情况，如果二者其他不相同，那么更加可行了。

思路还是有点难想的，就当作刷新一下自己的认知。

代码需要注意，图可能不连通。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
using namespace std;
#define Ls(i,l,r) for(int i=l;i<=r;++i)
#define Rs(i,l,r) for(int i=r;i>l;--i)
#define L(i,l) for(int i=0;i<l;++i)
typedef long long ll;
const int N=2510,M=20010,INF=0x3f3f3f3f;
int n,m,k,h[N],e[M],ne[M],idx,dis[N][N],q[N];
ll d[N],tu[3][N],res;
void add(int a,int b){
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void bfs(int s,int dis[]){
    memset(dis,0x3f,N*4);
    dis[s]=0;
    int hh=0,tt=0;
    q[tt++]=s;
    while(hh<tt){
        int u=q[hh++];
        for(int i=h[u];~i;i=ne[i]){
            int v=e[i];
            if(dis[v]==INF){
                dis[v]=dis[u]+1;
                q[tt++]=v;
            }
        }
    }
}
int main(){
    memset(h,-1,sizeof h);
    scanf("%d%d%d",&n,&m,&k);
    ++k;
    Ls(i, 2, n)scanf("%lld",d+i);
    while(m--){
        int a,b;
        scanf("%d%d",&a,&b);
        add(a,b);
        add(b,a);
    }
    Ls(i, 1, n)bfs(i,dis[i]);
    Ls(i, 2, n)
        Ls(j, 2, n){
            if(i!=j&&dis[1][i]<=k&&dis[i][j]<=k){
                ll v=d[i];
                if(v>=d[tu[0][j]])
                    tu[2][j]=tu[1][j],tu[1][j]=tu[0][j],tu[0][j]=i;
                else if(v>=d[tu[1][j]])
                    tu[2][j]=tu[1][j],tu[1][j]=i;
                else if(v>=d[tu[2][j]])tu[2][j]=i;
            }
        }
    ll a[3],b[3];
    Ls(i, 2, n)
        Ls(j, 2, n){
            if(i==j||dis[i][j]>k)continue;
            int cnta=0,cntb=0;
            L(k, 3)if(tu[k][i]&&tu[k][i]!=j)a[cnta++]=tu[k][i];
            L(k, 3)if(tu[k][j]&&tu[k][j]!=i)b[cntb++]=tu[k][j];
            L(k, cnta)
                L(l, cntb)
                    if(a[k]!=b[l]){
                        ll tmp=d[a[k]]+d[i]+d[j]+d[b[l]];
                        if(tmp>res)res=tmp;
                    }
        }
    printf("%lld",res);
    return 0;
}