最小表示法

最小表示法

思路

考虑将原串复制一遍，就可以得到所有循环同构串，然后先枚举两个位置 $i,j$，分别对应第一个和第二个位置。然后往后枚举，遇到第一个不同的位置，那么另外一个大的数对应的指针位置之前的每个循环同构串都不如第一个来的优，所以可以直接跳到这个位置的下一个位置。即假设 $s_i>s_j$，则 $j=k+1$，$k$ 表示从两个位置往后第一个不同的字符所枚举的个数。还有，如果 $i=j$，那么需要考虑将其中一个往后挪，再者如果 $k=n$ 了，那么说明原串是个循环串，如图：

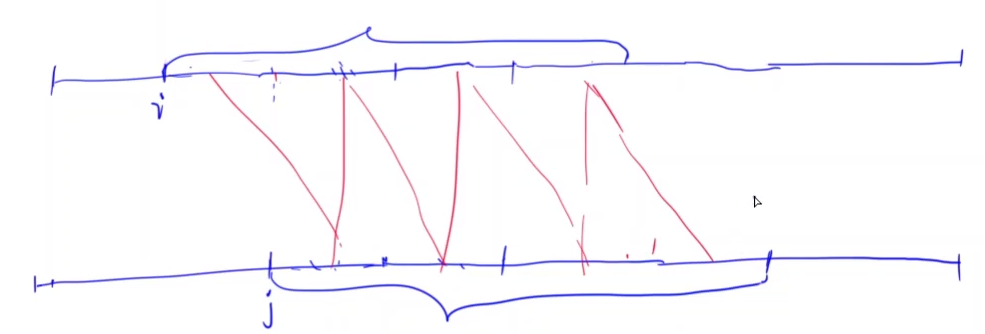
下图中第一条红线是由 $i,j$ 指针的移动定义得出的，第二条则是由同位置的数相等得到的，后面的也可以通过前两条关系类比推出，而且循环恰好是 $|i-j|$，这时退出，任意返回两指针任一即可。

#include<bits/stdc++.h>
using namespace std;
const int N=600010;
int n,s[N];
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;++i)scanf("%d",s+i);
	int i=1,j=2;
	memcpy(s+n+1,s+1,sizeof(n)*n);
	while(i<=n&&j<=n){
		int k=0;
		while(k<n&&s[i+k]==s[j+k])++k;
		if(k==n)break;
		if(s[i+k]<s[j+k])j+=k+1;
		else i+=k+1;
		if(i==j)++i;
	}
	i=min(i,j);
	for(int k=i;k-i+1<=n;++k)printf("%d ",s[k]);
	return 0;
}