希尔排序

插入排序的算法复杂度为O(n2)，但如果序列为正序可提高到O(n)，而且直接插入排序算法比较简单，希尔排序利用这两点得到了一种改进后的插入排序。

 

一. 算法描述

希尔排序：将无序数组分割为若干个子序列，子序列不是逐段分割的，而是相隔特定的增量的子序列，对各个子序列进行插入排序；然后再选择一个更小的增量，再将数组分割为多个子序列进行排序......最后选择增量为1，即使用直接插入排序，使最终数组成为有序。

增量的选择：在每趟的排序过程都有一个增量，至少满足一个规则 增量关系 d[1] > d[2] > d[3] >..> d[t] = 1 (t趟排序)；根据增量序列的选取其时间复杂度也会有变化，这个不少论文进行了研究，在此处就不再深究；本文采用首选增量为n/2,以此递推，每次增量为原先的1/2，直到增量为1；

下图详细讲解了一次希尔排序的过程：

 

 

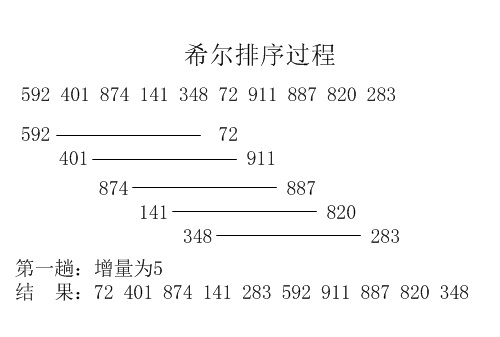
二. 算法分析

 

 

平均时间复杂度：希尔排序的时间复杂度和其增量序列有关系，这涉及到数学上尚未解决的难题；不过在某些序列中复杂度可以为O(n1.3);

空间复杂度：O(1)  

稳定性：不稳定

代码实现

 public static void ShellSort(int[] array)
        {
            //分组
            int step = array.Length / 3;
            while (step >= 1)
            {
                for (int i = step; i < array.Length; i++)
                {
                    int temp = array[i];
                    int j = 0;
                    for (j = i - step; j >= 0 && temp <= array[j]; j -= step)
                    {
                        array[j + step] = array[j];
                    }
                    array[j + step] = temp;
                }
                step = step / 3;
            }
        }

        -------------内层循环解释
         我们知道希尔排序是把数组分成step个数列，
       当前的temp就是当前数列的最后一个值，就是array[j + step],而这个数列的开头就是array[j]
      一般交换两个数需要一个第三个变量。在这里返现没有给array[j] 赋值，
       而此处的奥妙在与j = j - step 这个式子，假设当前的temp<<array[j] 不成立，跳出了循环
         在循环外面的 array[j + step] = temp; 又是上面意思
         在内循环中j = j - step的值已经改变 array[j + step] 里面的j + step就是当前数列的开始的位置。
        而temp又是当前的数列最后一个数的值。完成了交换。
        2：当前的内循环中temp<array[j]成立，进入到当前数列的上一个数列。此时的array[j]就是上一个数列的开始数的值。
        把数列首部的值赋值给尾部
        程序继续运行。判断条件不成立，把temp的值赋值给array[j + step]，上面已经说过了j + step就是当前的数列的位置，
        不懂的j + step，举个列子 在内循环中的j=0, j-5=-5;跳出循环 -5+5=0.