HDU4745--区间DP+回文串

　　这题的题意为，给你一个环状的字符串，有两只兔子分别从某任意的石头上开始跳跃。一只顺时针跳、一只逆时针跳。两只兔子每一次落脚处石头的质量都相同。兔子要一步一步的跳，且不能跳到之前跳到过的地方。总的来说，就是一只兔子最多就只能跳一整圈。每一次两只兔子落点的权值都相同，问兔子最多可以跳几次。这一题可以简化，用区间DP来求所有区间内的最长回文串长度。之后一遍for循环遍历，把区间[0,n-1]划分成[0,k]和[k+1,n-1]。找到这两个区间回文串长度和的最大值，即为答案。证明如下：

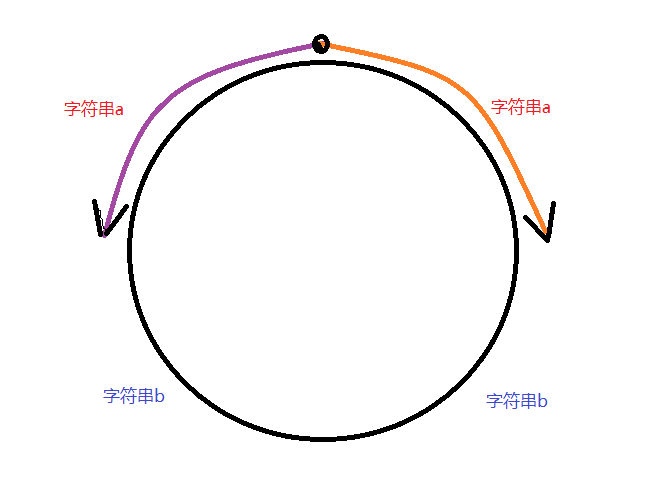
我们把区间分成了两部分   我们假设是串A和串B   我们可以把串A分成镜面对称的字符串a和字符串a，同理分解B。相当于拆成了43个串，但a和a连续  b和b连续。两个兔子设为从同一点出发。概念如图所示。

因此，求得A和B的最大回文长度之和，即求到了结果。代码如下：

#include<iostream>
#include<string.h>
using namespace std;
int T,i,j,k,l,n,m;
int a[1050][1050];
int c[1050];
int main()
{
    
    while(cin>>n&&n!=0)
    {
        memset(a,0,sizeof(a));
        for(i=0;i<n;i++) cin>>c[i];
        for(i=0;i<n;i++) a[i][i]=1;
        for(i=n-2;i>=0;i--)
        for(j=i+1;j<n;j++)
        {
            if(c[i]==c[j]) a[i][j]=a[i+1][j-1]+2;
            else a[i][j]=max(a[i+1][j],a[i][j-1]);
        }
        int ans=1;
        for(i=0;i<n-1;i++) ans=max(ans,a[0][i]+a[i+1][n-1]);
        cout<<ans<<endl;
        
    }
}