算法之动态规划（DP）求解完全背包问题（状态转移式方程推导）

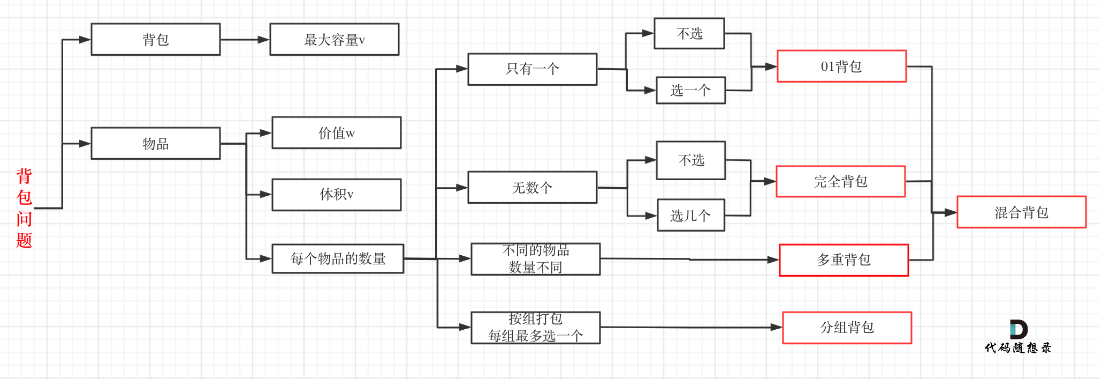
完全背包是01背包的进阶版。在这里补充一下代码随想录的完全背包状态转移式的推导。有兴趣的可以先看一看原版。

1. 状态转移方程
   状态：dp[i][j] 选择前i个物品，容量为j的背包时 所选物品价值总和最大。
   状态转移：
   dp[i][j]=max(dp[i-1][j-k* v[i]]+k* w[i]) (k=0,1,2,3...) (j-k* v[i]>0)

2. 方程优化
   dp[i][j]=max(dp[i-1][j]，dp[i-1][j- v[i]]+ w[i]，dp[i-1][j- 2* v[i]]+ 2* w[i]，....) --->(1)
   dp[i][j-v[i]]=max(dp[i-1][j-v[i]]，dp[i-1][j- 2* v[i]]+ w[i]，dp[i-1][j- 3* v[i]]+ 2* w[i]，....)
   dp[i][j-v[i]]+w[i]=max(dp[i-1][j-v[i]]+w[i]，dp[i-1][j- 2* v[i]]+ 2 * w[i]，dp[i-1][j- 3* v[i]]+ 3* w[i]，....) --->(2)
   结合（1）（2）可得：
   dp[i][j]=max（dp[i-1][j]，dp[i][j-v[i]]+w[i]）;

3. 对比01背包

   • dp[i][j]=max（dp[i-1][j]，dp[i-1][j-v[i]]+w[i]）(01背包)
   • dp[i][j]=max（dp[i-1][j]，dp[i][j-v[i]]+w[i]）(完全背包)

   发现了区别在下标从i-1变为i。为什么呢？
   f[i][j - v[i]] 已经将除去1个物品i时的所有最优解已经求出来了，因此在计算f[i][j]时，无需再重复计算k=2,3,4,5…时的值了。

• 代码：

// 先遍历物品，在遍历背包
void test_CompletePack() {
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    int bagWeight = 4;
    vector<int> dp(bagWeight + 1, 0);
    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        for(int j = weight[i]; j <= bagWeight; j++) { // 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    cout << dp[bagWeight] << endl;
}
int main() {
    test_CompletePack();
}