李宏毅深度学习笔记-Transformer
Transformer英文的意思就是变形金刚,Transformer现在有一个非常知名的应用,这个应用叫做BERT,BERT就是非监督的Transformer,Transformer是一个seq2seq model with “self-attention"。Transformer在seq2seq model里面大量用到了self-attention这种特别的层。
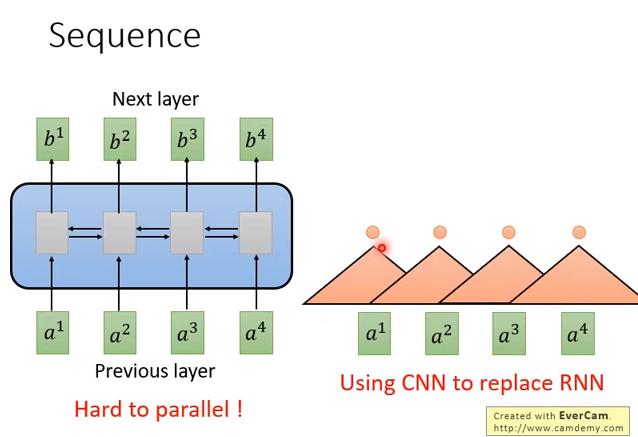
一般讲到处理sequence,最常想到的神经网络架构是RNN,有时候用单向的,有时候用双向的。
RNN的输入是一串向量sequence,输出是另外一串向量sequence。
如果是单向RNN,在输出\(b^4\)的时候,机器已经把\(a^1\)到\(a^4\)都看过,输出\(b^3\)的时候,把\(a^1\)到\(a^3\)都看过。
如果是双向RNN,当输出每个\(b^1\)到\(b^4\)的时候,机器把整个\(a^1\)到\(a^4\)都看过。
RNN的问题是不容易并行化。假设你要计算\(b^4\),在单向RNN下,你要先看\(a^1\)、再看\(a^2\)、再看\(a^3\)、再看\(a^4\),你才能把\(b^4\)计算出来。
那么怎么办呢?有人提出拿CNN来代替RNN。input同样是\(a^1\)到\(a^4\),但用CNN来处理。上图三角形代表一个filter,filter的输入是sequence中的一小段,比如吃三个向量作为输入,然后输出一个数值(三个向量串起来,和filter里面的参数做点积)。然后把filter扫过sequence,filter可以不只一个。
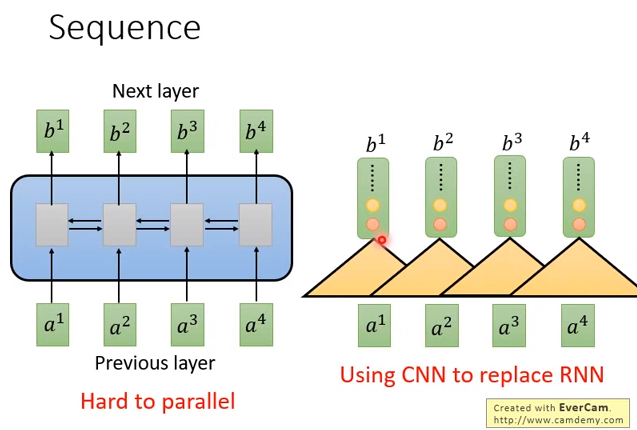
会有红色的filter,也会有黄色的filter,产生另外一排不同的数字。用CNN确实也可以类似RNN处理一个sequence input,输出一个sequence。表面上CNN和RNN可以做到同样的输入,有同样的输出。
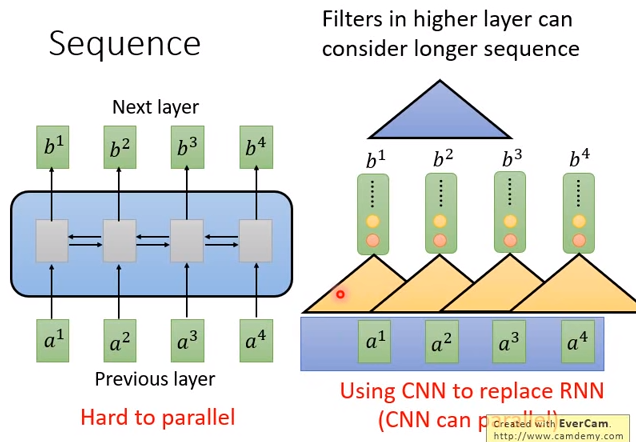
但是CNN只能考虑非常有限的内容,因为每个filter只考虑了三个向量,不像RNN可以考虑整个句子。但是CNN也不是没有办法考虑更长时间的信息(依赖),只要叠很多层的CNN,上层的filter就可以考虑比较多的信息。
比如上图第二层的CNN,第二层的input是第一层的output,蓝色的filter会看\(b^1、b^2、b^3\) ,而\(b^1、b^2、b^3\)是根据\(a^1、a^2、a^3、a^4\)决定的。等同于蓝色的filter已经看了所有的向量。
CNN的好处是可以并行的,不需要等第一个filter计算完之后再算第二个filter,全部的filter可以同时计算。也不需要等红色的filter算完,再算黄色的filter,它们可以同时计算。
但是CNN有个缺点是,一定要叠很多层,才能看到长期的信息。
Self-Attention
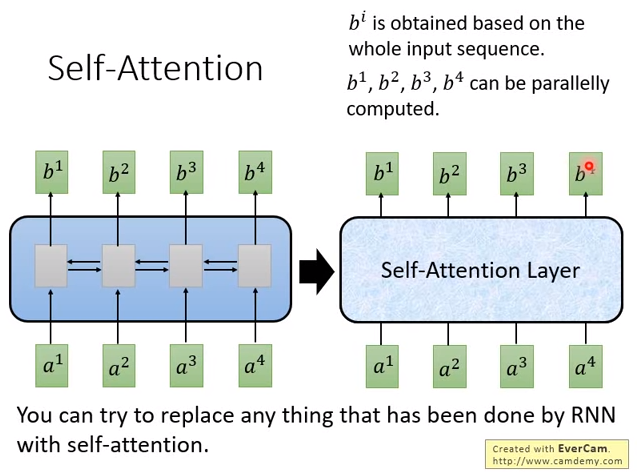
self-attention想要取代原来RNN做的事情。输入是一个sequence,输出是另一个sequence。特别的地方是,和双向RNN(每个输出都看过所有的输入)有同样的能力,每个输出也看过整个输入sequence。但是神奇的是,\(b^1\)到\(b^4\)是同时计算的。
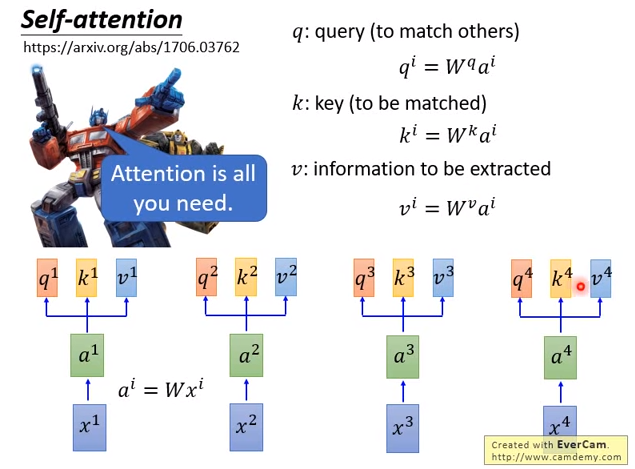
self-attention怎么做的呢?
首先input是\(x^1\)到\(x^4\),是一个sequence。
每个input先通过一个embedding变成\(a^1\)到\(a^4\) ,然后丢进self-attention layer。
self-attention layer里面,每一个input分别乘上三个不同的transformation(matrix),产生三个不同的向量。这个三个不同的向量分别命名为\(q、k、v\) 。
- \(q\) 代表query,要去match其他人,把每个input \(a^i\)都乘上某个matrix \(W^q\),得到\(q^i\) (\(q^1\)到\(q^4\))
- \(k\) 代表key,拿来被query match的,每个input \(a^i\)都乘上某个matrix \(W^k\),得到\(k^i\) (\(k^1\)到\(k^4\))
- \(v\) 代表information,是被抽取出来的东西,每个input \(a^i\)都乘上某个matrix \(W^v\),得到\(v^i\) (\(v^1\)到\(v^4\))
现在每个时刻,每个\(a^i\)都有\(q、k、v\)三个不同的向量。
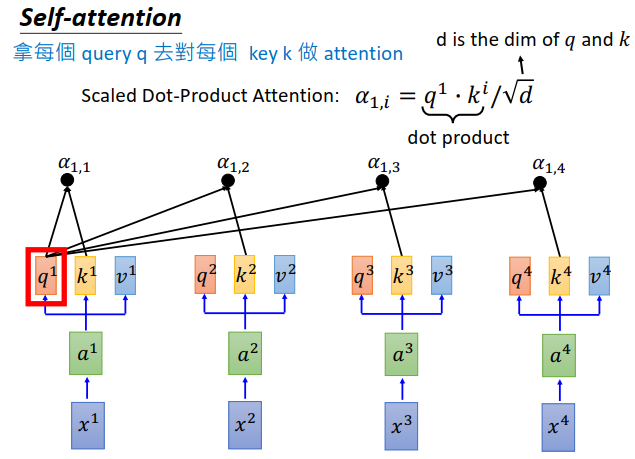
接下来要做的事情是拿每一个\(q\)对每个k做attention。attention是吃两个向量,output一个分数,告诉你这两个向量有多匹配,至于怎么吃这两个向量,则有各种各样的方法,比如可以做点积。
- 把\(q^1\)拿出来,对\(k^1\)做attention得到一个分数\(\alpha_{1,1}\)
- \(q^1\)和\(k^2\)也做一个attention得到一个分数\(\alpha_{1,2}\)
- \(q^1\)和\(k^3\)也做一个attention得到一个分数\(\alpha_{1,3}\)
- \(q^1\)和\(k^4\)也做一个attention得到一个分数\(\alpha_{1,4}\)
attention计算方法如上图所示,\(q^1\)和\(k^i\)做点积,然后除以\(\sqrt{d}\)
\(d\)是\(q\)跟\(k\)的维度,因为\(q\)要跟\(k\)做点积,所以维度是一样的。
为什么要除以\(\sqrt{d}\) ?
一个直观解释是\(q\)跟\(k\)的点积,会随着它们的维度增大而增大,除以\(\sqrt{d}\) 有一种标准化的直觉。
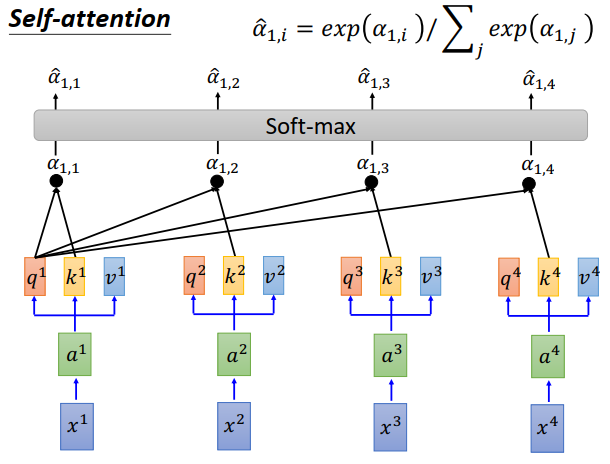
接下来\(\alpha_{1,1},\alpha_{1,2},\alpha_{1,3},\alpha_{1,4}\)通过一个softmax layer 得到 $ \hat \alpha_{1,1},\hat \alpha_{1,2},\hat \alpha_{1,3},\hat \alpha_{1,4}$
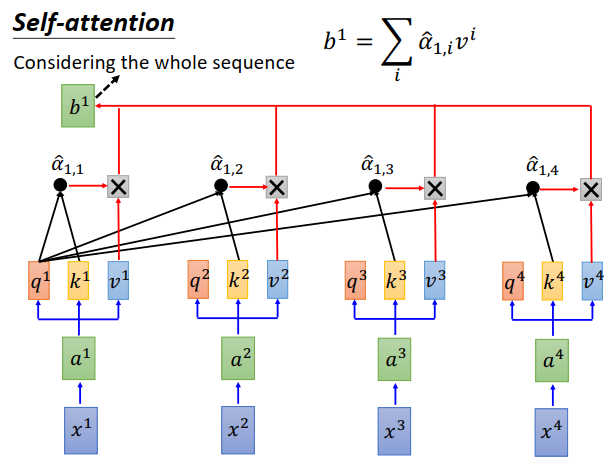
然后拿 \(\hat \alpha_{1,1},\hat \alpha_{1,2},\hat \alpha_{1,3},\hat \alpha_{1,4}\)分别和每一个\(v^i\)相乘。即\(\hat \alpha_{1,1}\)乘上\(v^1\),\(\hat \alpha_{1,2}\)乘上\(v^2\),\(\hat \alpha_{1,3}\)乘上\(v^3\),\(\hat \alpha_{1,4}\)乘上\(v^4\),最后相加起来。等于\(v^1\)到\(v^4\)拿 \(\hat \alpha_{1,1},\hat \alpha_{1,2},\hat \alpha_{1,3},\hat \alpha_{1,4}\)做加权求和,得到\(b^1\)。
刚才讲说self-attention就是输入一个sequence,输出也是一个sequence,那么现在就得到sequence的第一个向量\(b^1\) 。
但是你会发现,在产生\(b^1\)的时候,用了整个sequence的信息,看到了\(a^1\)到\(a^4\)的信息。
如果你不想考虑整个句子的信息,只想考虑局部信息,只要让\(\hat \alpha_{1,i}\)的值为0,意味着不会考虑\(a^i\)的信息。
如果想考虑某个\(a^i\)的信息,只要让对应的\(\hat \alpha_{1,i}\)有值即可。
所以对self-attention来说,只要它想看,就能用attention看到,只要自己学习就行。
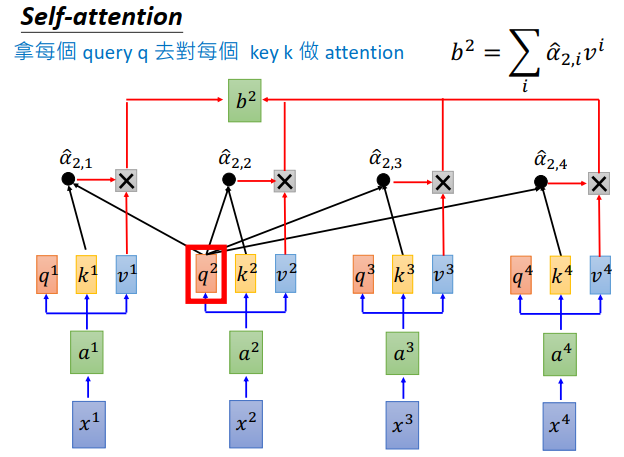
在同一时间,也可以计算\(b^2\),就是拿\(q^2\)跟\(k^1,k^2,k^3,k^4\)做attention得到 \(\hat \alpha_{2,1},\hat \alpha_{2,2},\hat \alpha_{2,3},\hat \alpha_{2,4}\),再拿\(\hat \alpha_{2,1},\hat \alpha_{2,2},\hat \alpha_{2,3},\hat \alpha_{2,4}\)跟\(v^1,v^2,v^3,v^4\)做加权求和得到\(b^2\)。
用同样的方法可以把\(b^3,b^4\)也算出来。
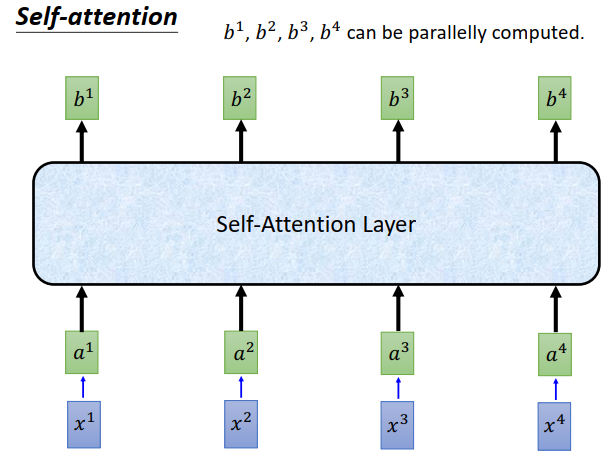
input一个sequence \(a^1\)到\(a^4\),得到另外一个sequence \(b^1\)到\(b^4\) ,self-attention 做的事情跟RNN是一样的,只不过计算attention是可以并行的。
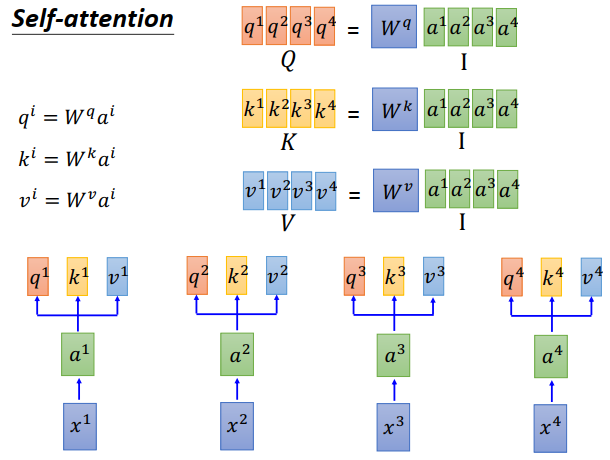
接下来要更清楚的说明,self-attention是怎么做并行的。
-
刚才说过,\(a^1,a^2,a^3,a^4\)乘以一个矩阵\(W^q\)变成\(q^1,q^2,q^3,q^4\)。
-
那么可以把\(a^1,a^2,a^3,a^4\)拼起来变成一个matrix \(I\),\(q^1,q^2,q^3,q^4\)拼起来变成\(Q\)
同理对
- \(a^1,a^2,a^3,a^4\)串起来,乘上\(W^k\),得到\(K\),\(K\)的每一列就是每个位置的一个key
对value来说也是一样
- \(a^1,a^2,a^3,a^4\)串起来,乘上\(W^v\),得到\(V\)所有位置的value
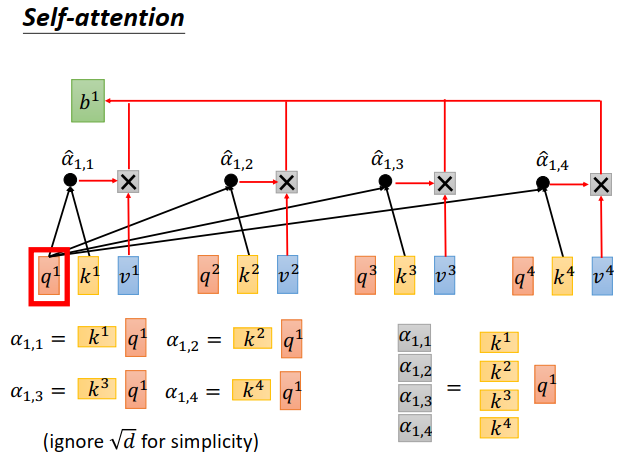
刚才说,拿\(q^1\)去对每个\(k\)做attention(就是点积),这里我们省略根号d。
\(q^1\)和\(k^1\)做点积,就是把\(k^1\)转置,然后乘以\(q^1\),得到\(\alpha_{1,1}\)
\(q^1\)和\(k^2\)做点积,得到\(\alpha_{1,2}\)
\(q^1\)和\(k^3\)做点积,得到\(\alpha_{1,3}\)
\(q^1\)和\(k^4\)做点积,得到\(\alpha_{1,4}\)
你会发现都是拿\(q^1\)来做计算,那么把所有的\(k\)拼在一起(每个\(k\)是矩阵的一行)变成一个矩阵。这个矩阵乘上\(q^1\),结果就是一个向量(\(\alpha_{1,1}\)到\(\alpha_{1,4}\)),\(\alpha_{1,1}\)到\(\alpha_{1,4}\)的计算是可以并行的。
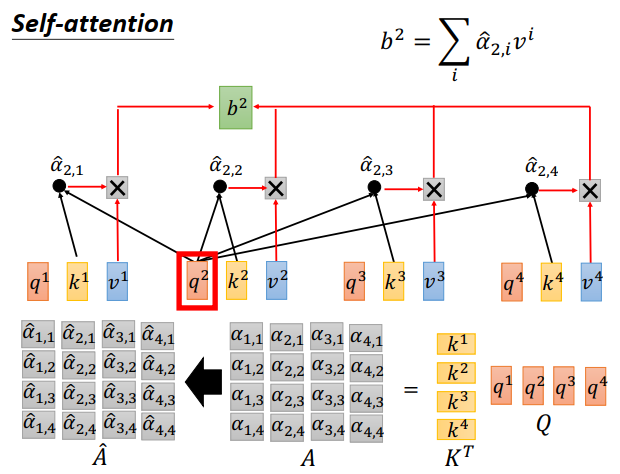
接下来把\(q^2\)拿出来,做的事情是和\(q^1\)一样的,\(q^3,q^4\)也是同理。那么计算attentin的过程,就是把矩阵K做一个转置,然后乘上Q,得到attention A。有N个input,那么attention 就是N*N矩阵,接下里做softmax得到\(\hat A\)。
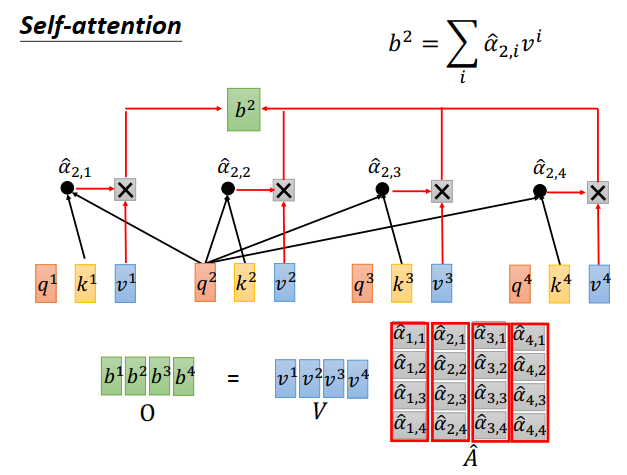
接下来要把\(v^1\)到\(v^4\),根据\(\hat \alpha\)做加权求和。
把矩阵\(V\)拿出来,每个列都是一个向量\(v^i\),乘上矩阵\(\hat A\) 得到self-attention的输出\(O\)。
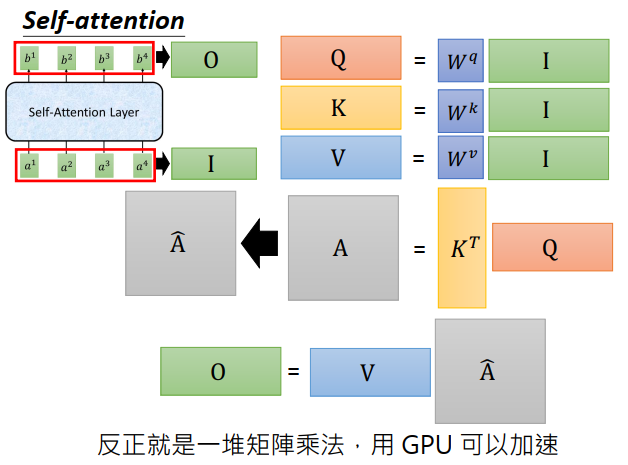
再回顾一下刚才的运算。整个self-attention的输入是一个矩阵\(I\),输出是一个矩阵\(O\)。
接下来要看看\(I\)到\(O\),中间self-attention做了哪些事情。
- 首先input \(I\)会乘上三个不同的矩阵\(W^q,W^k,W^v\),得到三个矩阵\(Q、K、V\),这三个矩阵的某个列,就代表了某个位置的query,key和value。
- 接下来\(K\)转置乘上\(Q\)得到attention矩阵\(A\),\(A\)中的每个元素代表了现在input sequence 两两之间的attention。\(A\)做sotfmax得到\(\hat A\)
- 然后\(\hat A\) 乘上\(V\)得到\(O\)
你会发现self-attention中做的就是一连串的矩阵乘法,可以用GPU加速。
Multi-head self-attention
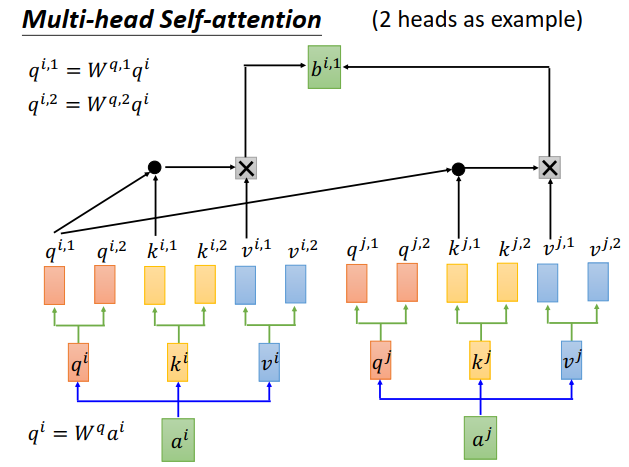
self-attention有个变形叫做Multi-head self-attention。这里用有两个head的情况来举例。
刚才说,每个\(a^i\)都会得到\(q^i、k^i、v^i\)。
在2个head的情况下,你会进一步把\(q^i\)分裂,变成\(q^{i,1}、q^{i,2}\),做法是\(q^i\)可以乘上两个矩阵\(W^{q,1}、W^{q,2}\)。
\(k^i、v^i\)也一样,产生\(k^{i,1}、k^{i,2}\)和\(v^{i,1}、v^{i,2}\)。
但是现在\(q^{i,1}\)只会对\(k^{i,1}、k^{j,1}\)(同样是第一个向量)做attention,然后计算出\(b^{i,1}\)
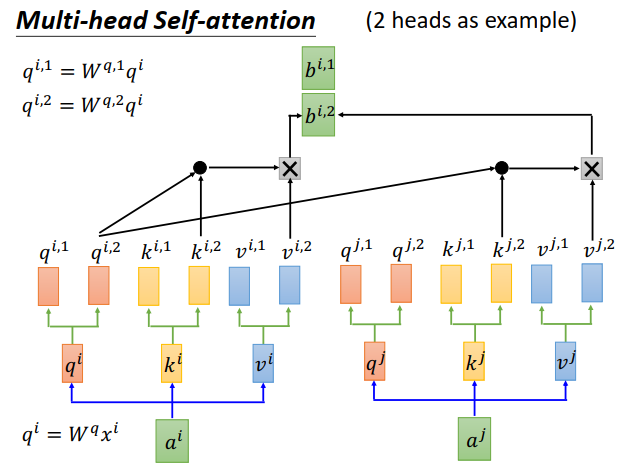
\(q^{i,2}\)只会对\(k^{i,2}、k^{j,2}\)做attention,然后得到\(b^{i,2}\)。
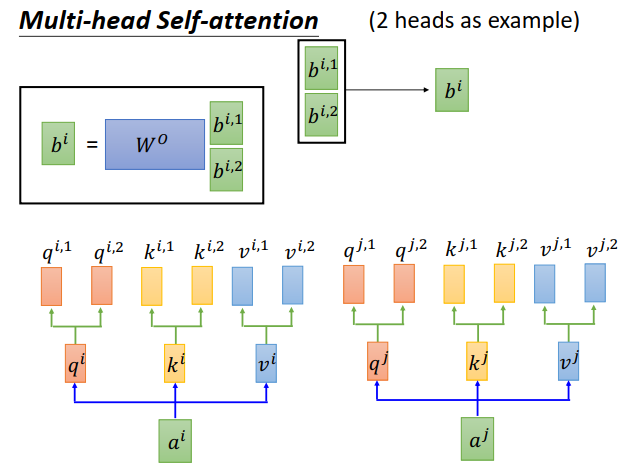
然后把\(b^{i,1}、b^{i,2}\)接在一起,如果你还想对维度做调整,那么再乘上一个矩阵\(W^O\)做降维就可以了。
那么做Multi-head有还什么好处呢?
有可能不同的head关注的点不一样,比如有的head想看的是local(短期)的信息,有的head想看的是global(长期)的信息。有了Multi-head之后,每个head可以各司其职,自己做自己想做的事情。
当然head的数目是可以自己调的,比如8个head,10个head等等都可以。
仔细看一下self-attention layer,你会发现对self-attention来说,input的sequence的顺序是不重要的。
对一个时间点来说,它跟每个时间点都做了self-attention,跟它是邻居的东西,还是跟它是在天涯的东西都是一样的,所以并没有所谓位置的信息。对self-attention来说,input "A打了B"跟"B打了A"是一样的,但是这个显然不是我们想要的,我们希望把input sequence的顺序考虑进self-attention layer里去。
在原始的paper中说,在把\(x^i\)变成\(a^i\)后,还要加上一个\(e^i\)(要跟\(a^i\)的维度相同),\(e^i\)是人工设定的,不是学出来的,代表了位置的信息,所以每个位置都有一个不同的\(e^i\)。比如第一个位置为\(e^1\),第二个位置为\(e^2\)......。
把\(e^i\)加到\(a^i\)后,接下来的步骤就跟之前的一样。
通常这里会想,为什么\(e^i\)跟\(a^i\)是相加,而不是拼接,相加不是把位置信息混到\(a^i\)里去了吗
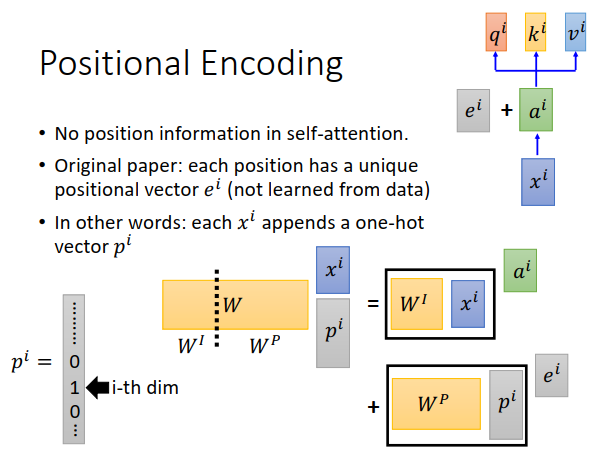
这个给一个跟原始paper不一样的想法,我们可以想象,给\(x^i\)再添加一个向量\(p^i\)(代表了位置信息),\(p^i\)是一个很长的向量,位置为1,其他为0。
\(x^i,p^i\)拼接后乘上一个矩阵\(W\),你可以想像为等于把\(W\)拆成两个矩阵\(W^I、W^P\),之后\(W^I\)跟\(x^i\)相乘+\(W^P\)跟\(p^i\)相乘。而\(W^I\)跟\(x^i\)相乘部分就是\(a^i\),\(W^P\)跟\(p^i\)相乘部分是\(e^i\) ,那么就是\(a^i+e^i\),所以相加也是说得通的。
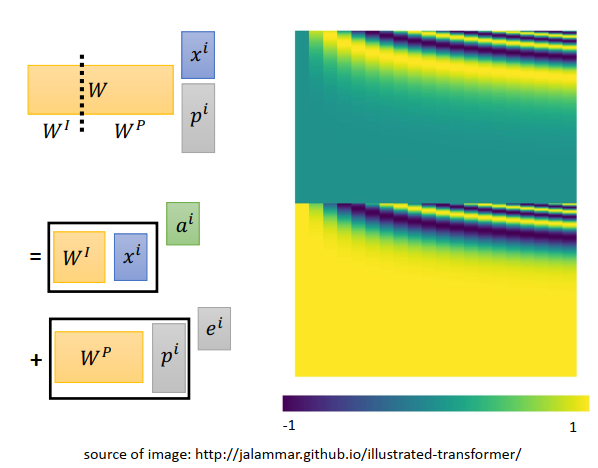
\(W^P\)你当然是可以学习的,但是有人做过实验,学出来的\(W^P\)效果并不好。
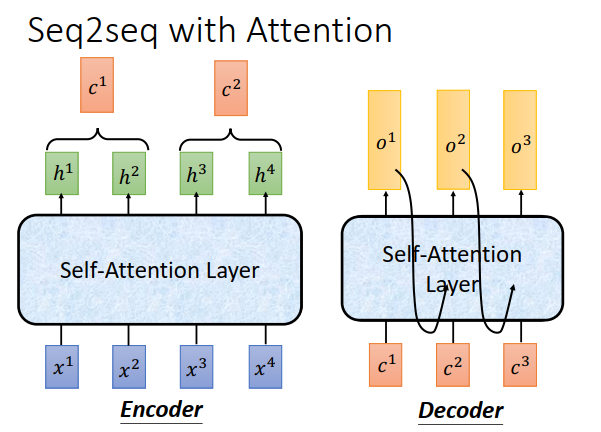
刚才讲可以把self-attention拿来取代RNN,接下来讲self-attention在seq2seq中是怎么被使用的。
我们讲过seq2seq有两个RNN,一个是encoder,一个是decoder(不仅会attent encoder的输入,也会attent decoder已经产生的output)
encoder中是一个双向RNN,现在可以用self-attention 取代掉,encoder中是一个RNN,也可以用self-attention取代。
简单的概念就是看到RNN,就用self-attention 取代。
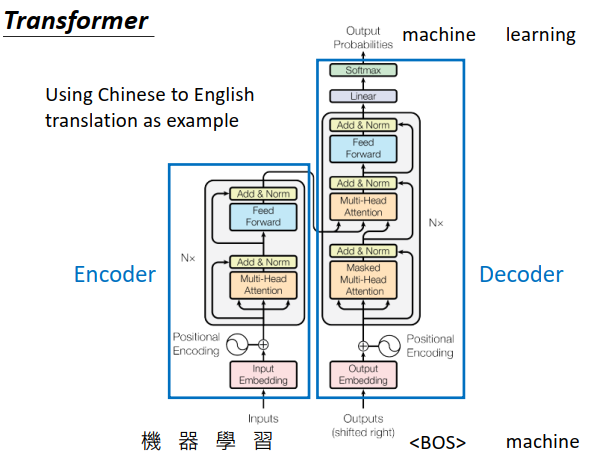
这个图讲的是一个seq2seq model。左半部是encoder,右半部是decoder。encoder的输入是机器学习(一个中文的character),decoder先给一个begin token
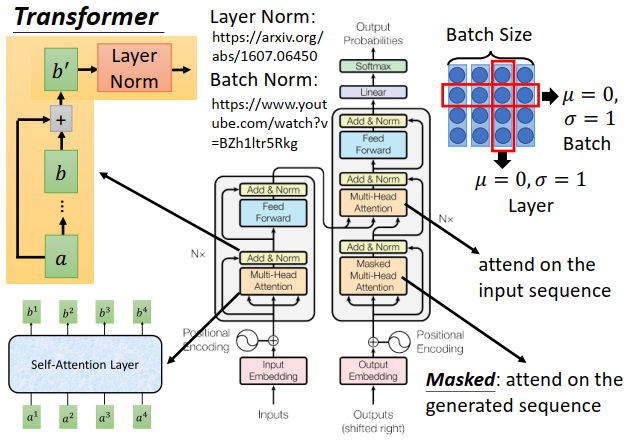
接下来看里面的每个layer在干什么。
先看encoder:
input通过一个input embedding layer变成一个向量,然后加上一个位置encoding向量
然后进入灰色的block,这个block会重复多次
- 第一层是Multie-head attention,input一个sequence,输出另一个sequence
- 第二层是Add&Norm
- 把Multie-head attention的input \(a\)和output \(b\)加起来得到\(b'\)(Add)
- 把\(b'\)再做layer Norm,上图右上方所示时候batch Norm(行,n样本一个维度)标准化,和layer(列,1个样本n维度)标准化。一般layer Norm会搭配RNN使用,也是这里使用layer Norm的理由
- 第三层是Feed Forward,会把sequence 的每个\(b'\)向量进行处理
- 第四层是另一个Add&Norm
再看decoder:
decoder的input是前一个时间点产生的output,通过output embedding,再加上位置encoding变成一个向量,然后进去灰色的block,灰色block同样会重复多次
- 第一层是Masked Multie-head attention,Masked的意思是,在做self-attention的时候,这个decoder只会append到已经产生的sequence,因为没有产生的部分无法做attention
- 第二层是Add&Norm
- 第三层是Multie-head attention,attend的是encoder部分的输出
- 第四层是Add&Norm
- 第五层是Feed Forward
- 第六层是Add&Norm
- 第七层是linear
- 最后是softmax
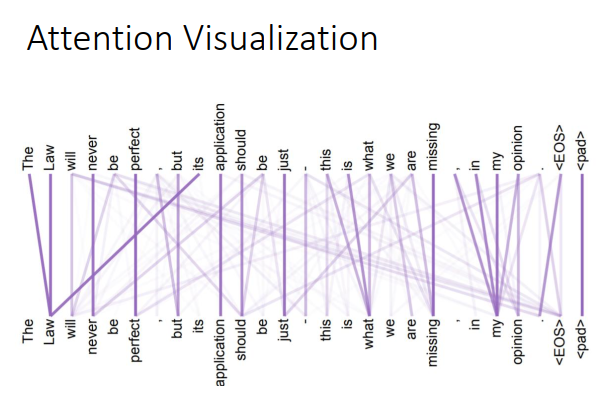
Transformer paper最后附上了一些attention的可视化,每两个word之间都会有一个attention。attention权重越大,线条颜色越深。

现在input一个句子(动物没走过这条路因为动物太累了),在做attention的时候,你会发现it attent到animal。
但是把tired换成wide(动物没走这过条路因为路太宽了),it会attent到street。
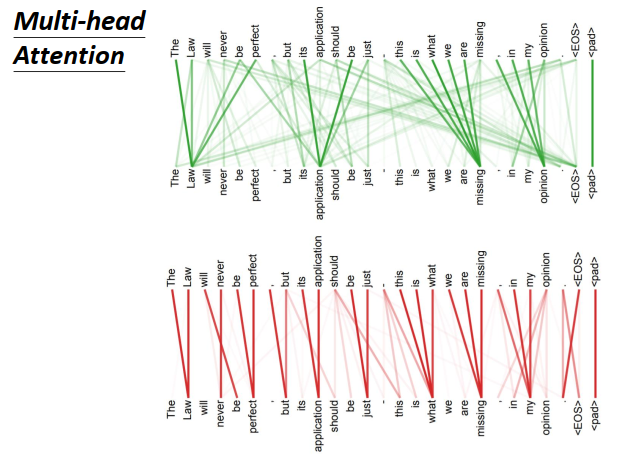
Multi-head self-attention每一组\(q,k\)都做不同的事情,这里告诉你,确实是这样。如上图所示,显然下面的一组query和key想要找的是local的信息。
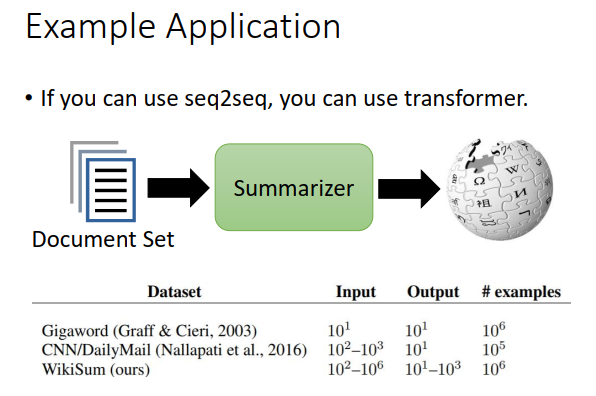
原来可以用seq2seq的任务都可以换成transformer。
惊人的是文章摘要,可以input一堆而不是一篇文章,output却是一篇文章的摘要。
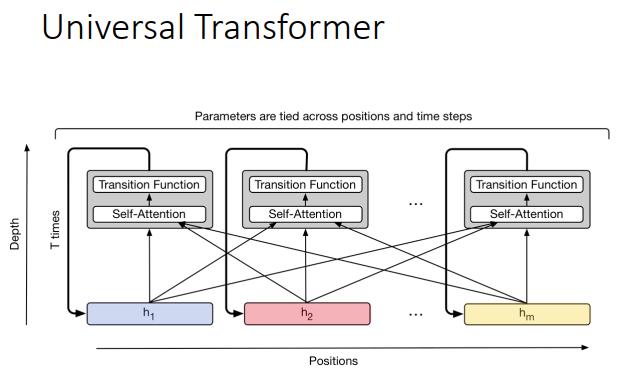
transformer有个进一步的变形叫做Universal Transformer。
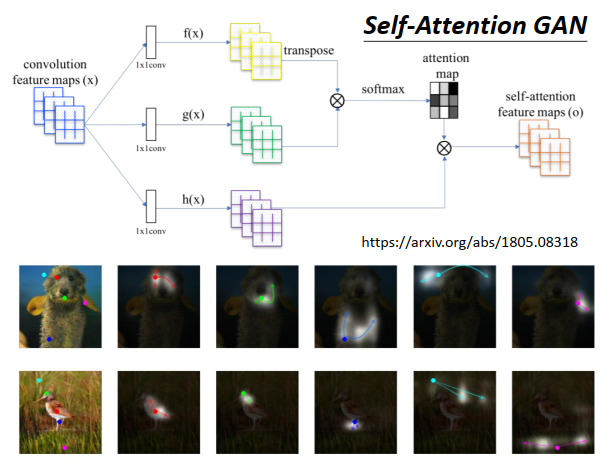
现在transformer也可以用在图像上。


