李宏毅深度学习笔记-深度学习技巧
深度学习的流程
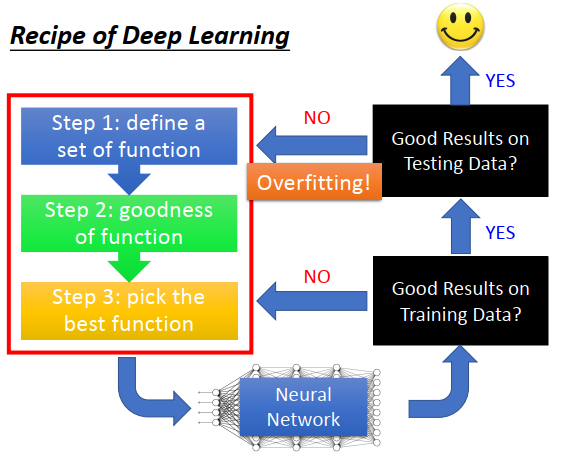
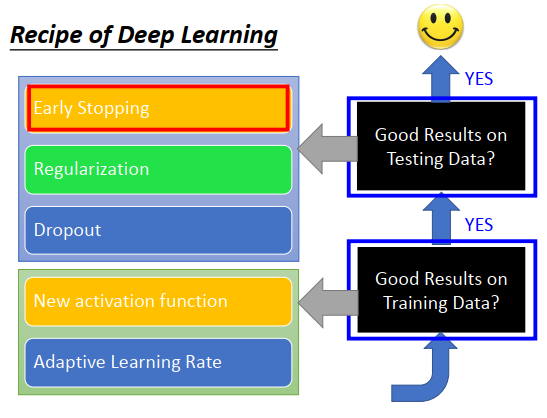
通过深度学习三部曲得到一个神经网络,接下来要做什么事情?
- 先检查神经网络在训练数据集上的结果好不好,不好则回头检查三部曲。过拟合在深度学习里面不是要先关注的问题,因为深度学习是一个不断迭代训练的模型,可能一开始训练精度很差,因此首先要考虑的是如何优化三部曲里面的东西。
- 训练精度好,再去检查测试精度,如果结果不好,再考虑过拟合。而且有时候使用新技术去优化过拟合,可能又会导致训练精度变差,这时候又要去检查训练精度。
- 训练精度和测试精度都好,才可以使用
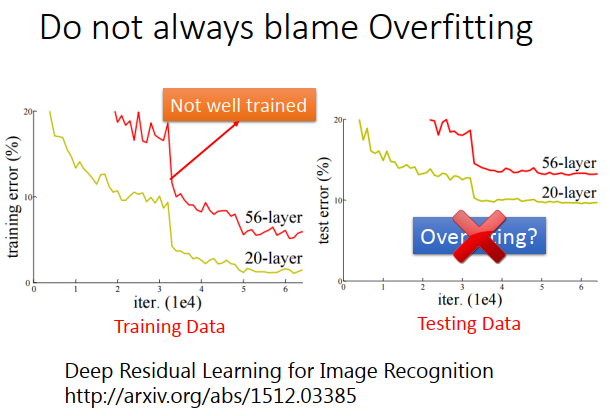
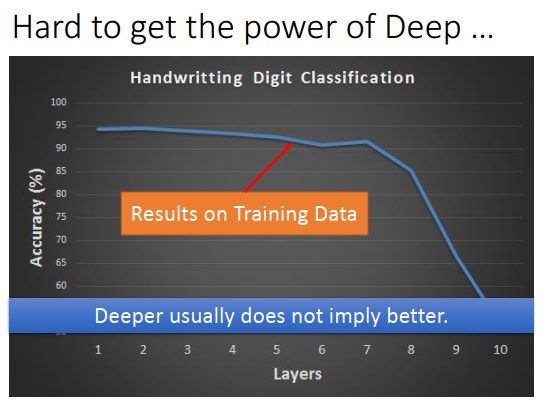
黄线是20层的神经网络,红线是56层的神经网络
是否会觉得56层神经网络效果差是由于过拟合?真的是这样吗?
在做test error的时候,先要去检查train error。有些方法不用做这种事,但是对于神经网络来说是要去做的。
有可能在训练数据上,56层的神经网络误差就很大。为什么会这样子?
可能有局部最小值、鞍点等种种问题,56层的神经网络可能卡在局部最小值,得到一组很差的参数。这个也不是欠拟合,因为56层本身参数量就很多。理论上20层神经网络能做到事情,56层神经网络也可以做到,只要前20层一样,后36层都是恒等式就可以。所以也不是欠拟合,就是没有训练好参数。像喷火龙一样,能力是够的,就是不想打。
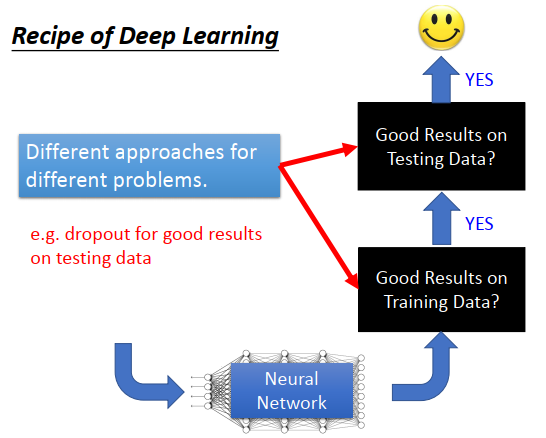
看到一个深度学习方法的时候,永远要先思考,这种方法用来解什么问题。
深度学习里有两个问题,一个是train set上不好,一个是test set上不好。一个方法不好的时候,往往针对其中一个问题来做处理。比如dropout,但是dropout是在test不好的时候用的,如何你train结果不好,再用dropout,只会导致train更差。
如何改进深度学习?
train 结果不好
新的激活函数
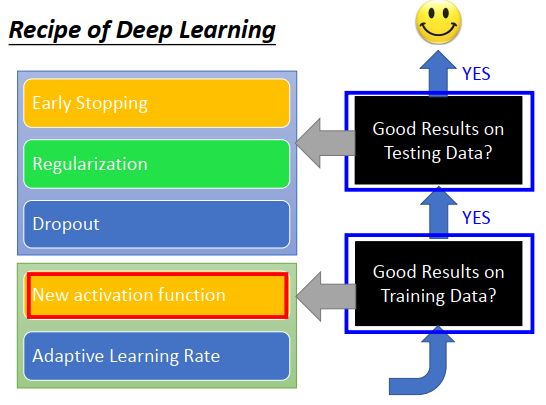
train 结果不好的时候,考虑是否网络结构没有设计好。比如激活函数不好,因此换一些新的激活函数。
1980年代比较常用的激活函数是sigmoid函数,为什么要用sigmoid?
在过去,会发现越深不一定意味着越好,如上图,layer越多,准确率会下降。可能会觉得是过拟合,但这个是train的结果。
梯度消失
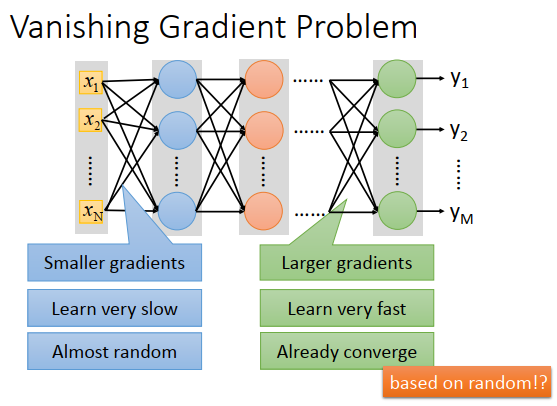
网络叠的很深的时候
- 靠近input的layer,参数对loss function的微分会很小,靠近output的layer,参数对loss function的微分会很大。
- 当设定同样的学习率时,靠近input的layer的参数update很慢,靠近output的layer的参数update很快
- 几次迭代下来,在input那边的参数还没怎么变动(还是近似random值),output那边的参数已经收敛了,然后loss 下降的很慢,处于一个局部最小点
为什么结果很差?
因为output附近参数的收敛,几乎是基于input附近参数的随机值。output就相当于是随机的
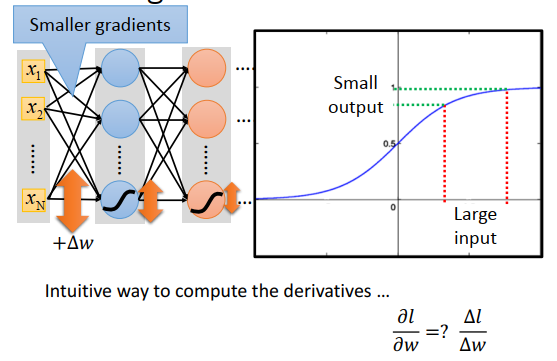
为什么会发生梯度消失?
直觉来想
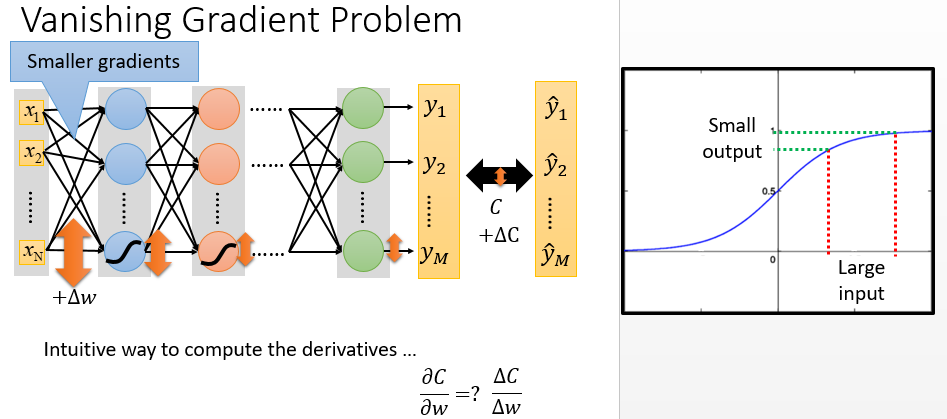
直觉的意思是说,对某个参数做个小小的变化,对cost的影响是怎么样,来看这个参数的梯度有多大
对第一个layer的某个参数\(+\Delta w\) ,即改变某个参数的权重,对某一个的神经元的output会有影响,但是影响是会衰减的。
为什么是衰减的?
看右上图是sigmoid的形状,sigmoid把\(-\infty\)到\(+\infty\)压缩到0,1。就算input的变化很大,output的变化也会变得很小。所以就算\(\Delta w\)造成\(w\)有很大变化,经过sigmoid之后,output变化也会衰减,且每通过一层的sigmoid,变化就衰减一次。如果神经网络很深,变化衰减的次数越多,直到最后对最终output的影响非常小。
也就是说在input层附近改一下参数,output层附近的output变化是很小的,因此对cost的影响也很小,自然梯度值也很小。
如何处理梯度消失

改一下激活函数,可能就可以处理这个问题
现在比较常用的就是ReLU激活函数,input>0时Input=output,input<0时output=0
选择ReLU有什么好处?
- 跟sigmoid比起来,运算很快,sigmoid里面还有指数运算
- 有一些生物上的原因
- ReLU等同于无穷多不同bias的sigmoid叠加
- 可以处理梯度消失问题
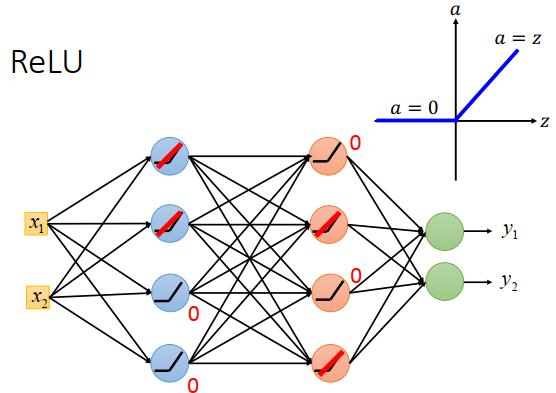
ReLU如何处理梯度消失问题?
查看一个使用ReLU作为激活函数的神经网络
ReLU当input>0时input=output,是线性的,当input<0时output=0。对那些output=0的神经元来说,对网络是没有一点影响的,对最终的output没有一点作用,就可以把这些神经元忽略掉。
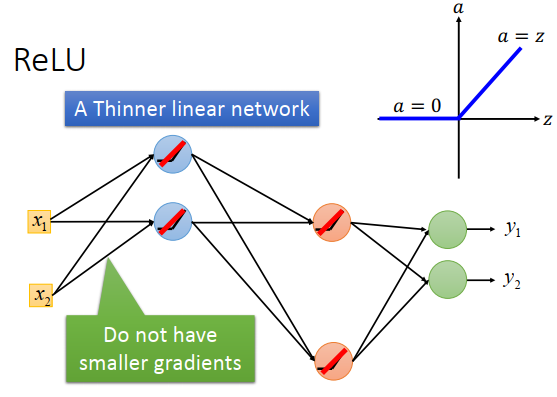
剩下的网络里面神经元的input=output,整个网络就是一个瘦长的线性网络
刚才说过的output衰减是由于input通过sigmoid,但是线性网络就不会有衰减问题
使用RelU变成了线性网络,但是我们要的不是一个线性网络,做深度学习就是不想函数是线性的,我们希望得到一个复杂的非线性函数,那使用ReLU不会有问题吗?不会让函数变得很弱吗?
对整个网络来说,整体还是非线性的。虽然input变化一点,output变化是线性的,但如果input变化的比较多,直接变到<0了,那整个神经元就没有用了,或者从没有用变到线性,所以整体上还是非线性的。
Relu在0点不可微啊?
实际中可以不用管这个点,>0的时候微分为1,<0的时候微分为0
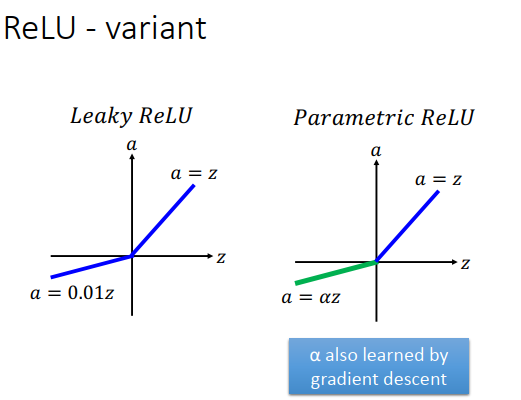
ReLU有很多变种
- input<0时微分=0,那就没办法update参数了,那么给input<0的微分为0.01,这个就是leaky ReLU
- 为什么就用0.01,不用0.07,0.08,有人就设置一个参数\(\alpha\),这个参数可以从train 中学习到,甚至每个神经元都可以有一个不同的\(\alpha\)
- Relu为什么是这个样子,有没有其他的样子,产生了Maxout,让网络自动学习激活函数,ReLU就是其中一个特例,即Maxout network 可以学出ReLU这样的激活函数,具体要取决于训练数据
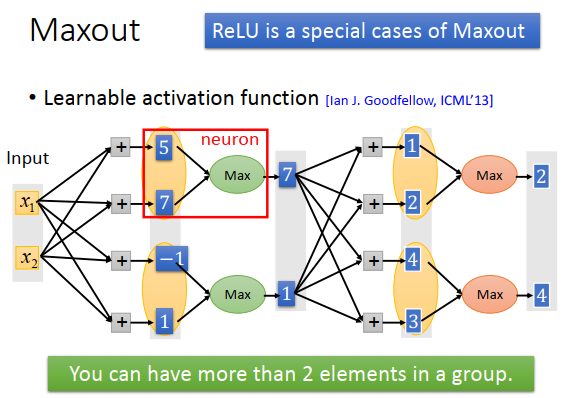
input乘以不同的权重得到5,7,-1,1,本来这些值是要通过激活函数的。在Maxout里面,把这些值group起来(哪些值被group是事先决定的),在group里面选择最大值作为output,这个跟max pool 是一样的。
把几个值组成一个group是超参数,可以3个,4个。
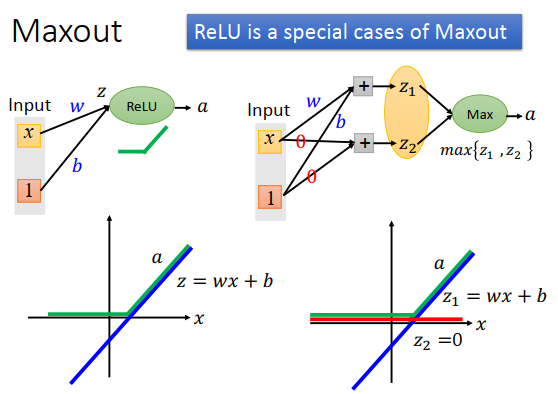
Maxout是可以做到Relu的功能的
ReLU:上左下图看到,z和x是线性的,z<0时a=0,z>0时a=z
Maxout:上右上图看到,假设计算\(z_2\) 的两个w和b=0,那么\(z_2=0\)。\(z_1\)和x的关系就是右下图蓝色线,\(z_2\)和x的关系是红色线,因为\(z_2=0\) 。Maxout是\(max\{z_1,z_2\}\) ,\(z_1>0\)时为\(z_1\),\(z_1<0\)时为\(z_2\) =0。只要把\(z_1\)的\(w,b\)等于Relu里z的\(w,b\),那么两者作用就是相等的
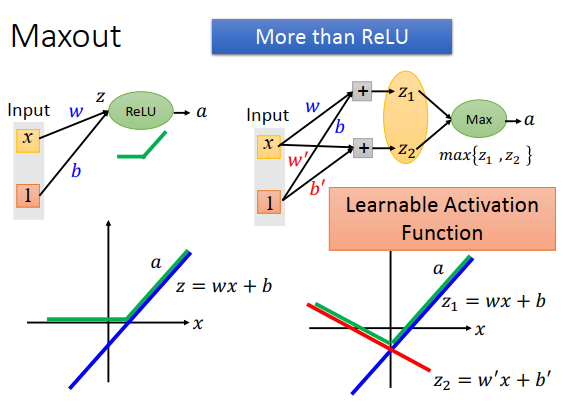
Maxout还可以做出不同的激活函数
\(w',b'\)不为0时,\(z_2\)和\(x\)的关系是红色线,那么Maxout的作用是绿色这条线,得到一个不一样的激活函数,由\(w,b,w',b'\)决定,即是由训练数据学习的
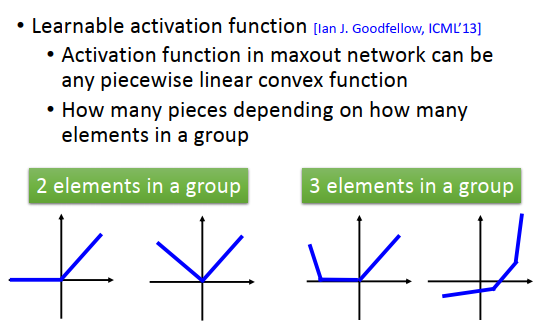
Maxout可以做出任意的分段凸激活函数
有多少个分段,取决于把多少个值组成一个group
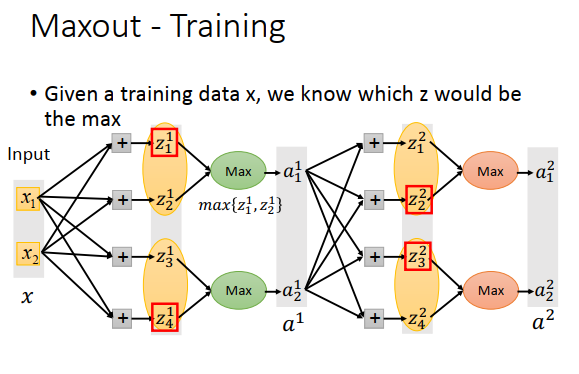
如何训练Maxout?有Max不能微分
假设比较大的是\(z_1^1\),等于\(a_1^1\);\(z_2^2=a_1^2\)
\(z_4^1=a_2^1;z_3^2=a_2^2\)
所以Max操作就是一个线性操作,只不过接的是前面group里较大的元素。那没有被接到的元素就没用了,可以去掉。
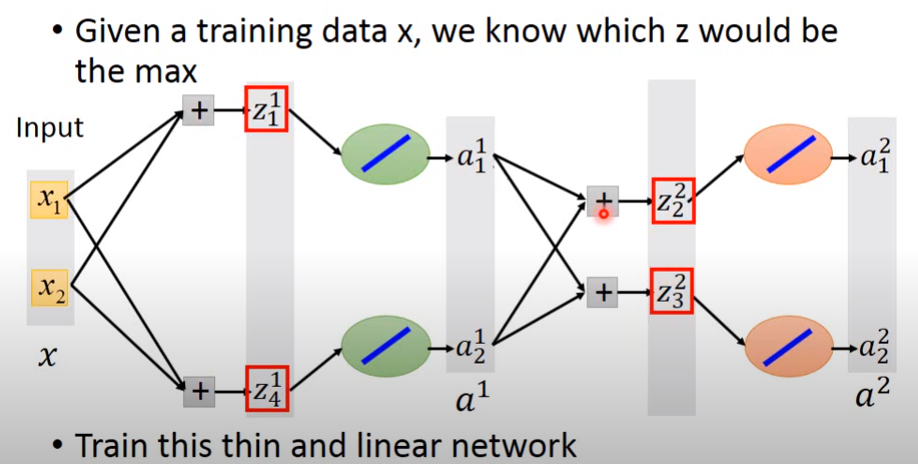
所以训练Maxout就相当训练一个细长的线性网络的参数,这些参数对应到group里面较大的元素
这里会有一个问题,没有被选择的元素对应的权重怎么训练?
这其实不是一个问题,因为不同的input,\(z_1^1,z_4^1,z_2^2,z_3^2\)是不同的,每次输入Input时,网络结构都是不一样的。如果有很多训练数据,每个权重都可以被训练到。
自适应学习率
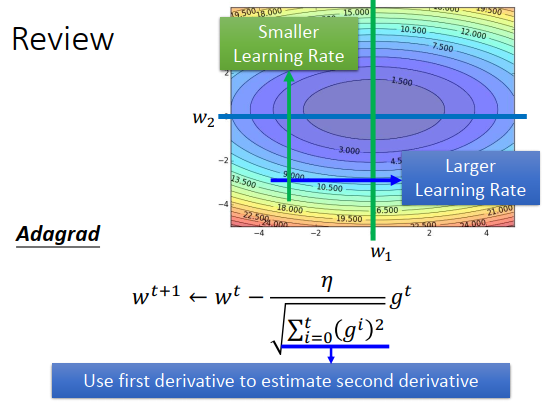
Adagrad每个权重有一个学习率,t+1次迭代的学习率等于 \(\eta\) 除以之前所有的梯度平方和
在\(w_1\)方向上梯度小,变化缓慢,那么给大的学习率;在\(w_2\)方向上梯度大,变化剧烈,那么给小的学习率
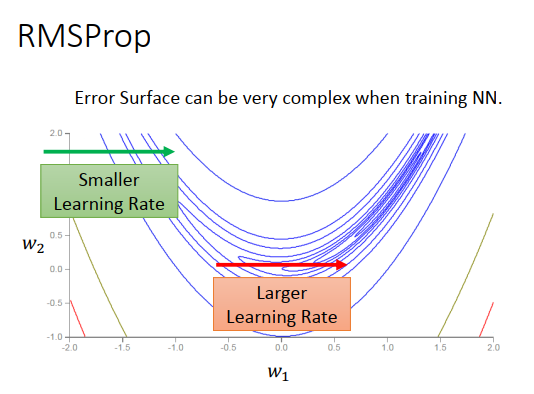
实际问题中,loss 不会是凸的,有各种奇怪的形状,比如上图这种月形
所有有可能在\(w_1\)一个方向上,有的区域很平缓,需要一个大的学习率,有的区域很陡峭,则需要一个小的学习率
仅仅使用Adagrad是不够的,需要更动态的调整学习率的方法,于是提出RMSProp方法。

固定的学习率\(\eta\) 除以 \(\sigma\) ,\(\sigma\)计算如上图所示,\(\alpha\)是人工调整的
原来Adagrad的分母是\(g^0,g^1,g^2...\)取平方和开根号
RMSProp的分母里,比如\(\sigma^2\)包含了\(g^2\),也包含了\(g^0,g^1\),因为\(\sigma^1\)是\(g^0,g^1\)计算出来的
不过RMSProp分母里还乘上了一个权重\(\alpha\) 和(\(1-\alpha\)),如果手动把\(\alpha\)调整小一点,则倾向于相信新的梯度
RMSProp一样是在算梯度的均方根,但是可以给现在的梯度一个大的权重,给过去的梯度一个小的权重
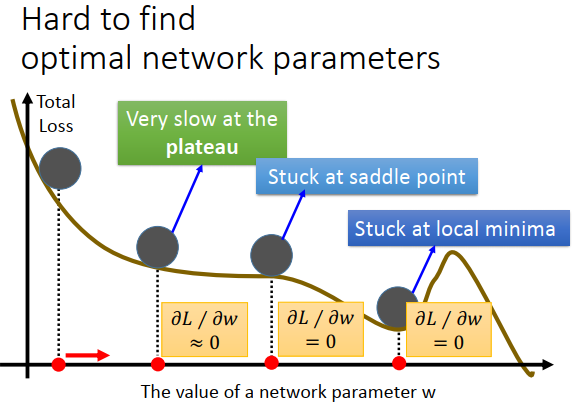
除了学习率的问题之外,也有其他问题,比如卡在局部极小点,鞍点和plateau(平稳区域)
Yann LeCun(CNN之父)提过,不用太担心局部最小值问题,在误差曲面上没有太多局部最小值。要是一个局部最小值,那在每个维度都必须是局部最小的形状(一个山谷的谷底),假设山谷谷底出现的概率是p,因为神经网络有很多的参数,假设有1000个参数,每个参数都要在谷底的概率是\(p^{1000}\) ,网络越大参数越多,出现的概率就越低,所以局部最小值在很大的神经网络里没有那么多,当训练走到一个认为是局部最小值的地方的时候,大概率是全局最小值或很接近全局最小值。
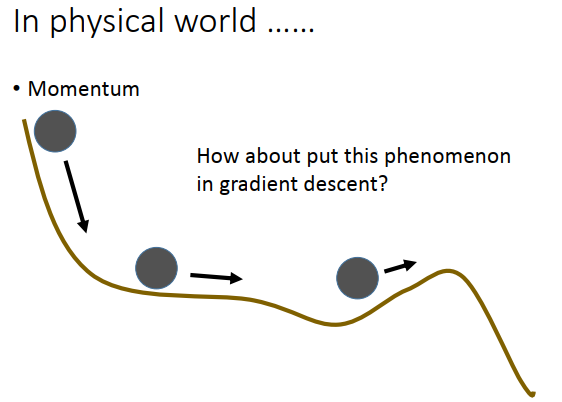
一个启发式的方法,来处理下局部最小值、鞍点、平稳区域的问题。
在真实世界里,把球从上图左上角丢下去,滚到平稳区域有惯性不会停下来,滚到上坡的地方,如果坡不是很陡,可以翻过这个坡,就可以走到比局部最小值更好的地方。我们可以把惯性这个性质融合到梯度下降里去,这个就叫做动量。
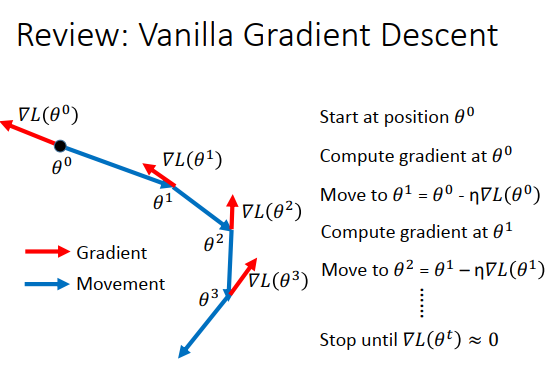
动量怎么做,先复习下一般的梯度下降。
选个参数初始值,计算梯度,参数往负梯度方向走一个步长\(\eta\)
重新计算梯度,参数走一个步长
再计算梯度,再走一个步长
直到梯度等于0或者趋近于0停止
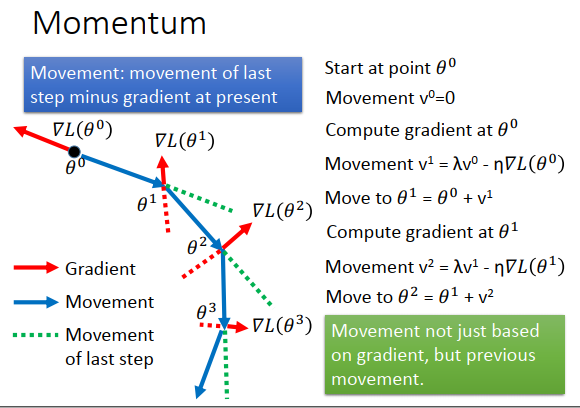
加上动量怎么做?
每一次移动的方向不再是只考虑梯度,而是现在的梯度方向加上前一个时间点移动的方向
选择一个初始值\(\theta^0\),用一个值\(v\) 记录前一个时间点移动的方向,初始的时候为\(v^0=0\)
计算\(\theta^0\)的梯度,上图红色箭头,现在移动的方向变为 \(v^1=\lambda v^0-\eta \Delta L(\theta^0)\),类似惯性
计算\(\theta^1\)的梯度,参数移动方向为\(v^2=\lambda v^1-\eta \Delta L(\theta^1)\)

另一个角度来理解动量
在第i个时间点移动的量\(v^i\),是过去算出来的梯度总和
$v^0=0 $
\(v^1=-\eta \Delta L(\theta^0)\)
\(v^2=-\lambda \eta \Delta L(\theta^0)-\eta \Delta L(\theta^1)\),有\(\theta^0,\theta^1\)的梯度,只不过权重不一样,\(\lambda<0\)时,越之前的梯度权重越小,越在意现在的梯度,不过之前的梯度也对现在update的方向有一些影响
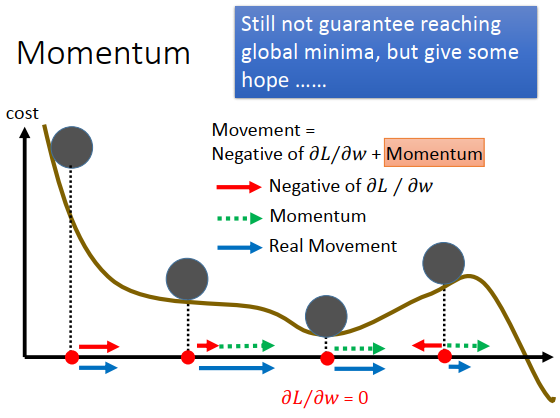
加入动量后,每次移动的方向是负梯度+动量
动量很强的话,有一定可能跳出局部最小值

RMSProp+Momentum 可以得到Adam
上图初始化里的\(m_0\)就是动量,\(v_0\)就是RMSProp里的\(\sigma\)
步骤里:
计算梯度\(g_t\)
根据\(g_t\)计算出\(m_t\) ,就是现在要走的方向,考虑过去要走的方向\(m_{t-1}\)+现在的梯度\(g_t\)
计算放在分母里的\(v_t\),是前一个时间点的\(v_{t-1}\)+现在的梯度平方\(g_t^2\)
然后计算RMSProp和Momentum没有的东西bias correction(偏差校正) \(\hat{m_t}\)和\(\hat{v_t}\)
test 结果不好
提前停止
上图的testing data不是测试集,而是验证集
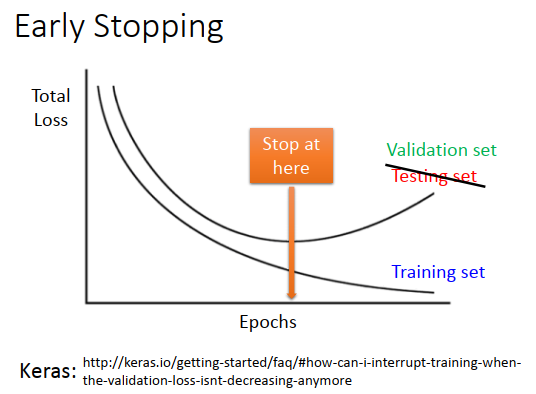
提前停止是什么意思?
随着训练次数变多,如果学习率比较适合的话,训练集总体损失是越来越小的。但是测试集和训练集的分布是不一样的,可能训练集总体损害减小,测试集总体损失反而变大。理想上,如果知道测试集总体损失的变化,那么训练应该停在测试损失最小的地方。但是实际上我们并不知道测试损失的情况,那么用验证集来检验这个事情。
用验证集模拟测试集,来做训练停止。
正则化
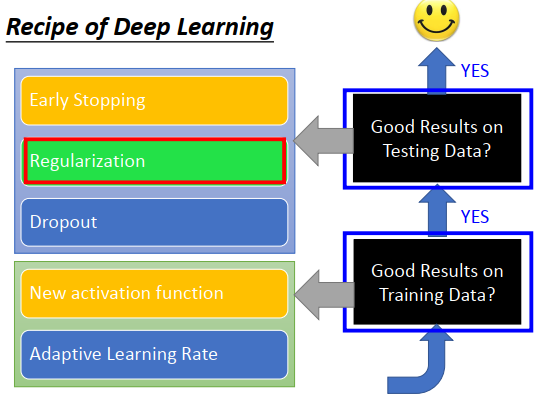

正则化重新定义了损失函数,原来的损失函数是\(L(\theta)\),再加上正则项,比如L2正则
加正则化项,一般不会考虑函数的偏差,因为加正则的目的是让函数变得更平滑,而偏差跟函数的平滑程度没有关系

如果加入L2正则项,微分会有怎么样的结果。
新的损失函数为\(L'(\theta)=L(\theta)+\lambda \frac{1}{2}||\theta||_2\),求梯度看上图
参数更新的式子变为 \(\large w^{t+1}=(1-\eta \lambda)w^t-\eta \frac{\partial L}{\partial w}\)
每次更新参数,先把原来的参数乘以\(1-\eta \lambda\) ,\(\eta\)是学习率(一个很小的值),\(\lambda\)也是一个很小的值(比如0.001)。
那么\(1-\eta \lambda\)是一个很接近1的值(比如0.99),那么每次更新参数,就会把原来的参数缩小为0.99倍,参数会越来越接近于0,不一定越来越小,如果\(w\)是负的就是变大。
那越来越接近于0,不是所有参数都变为0了吗?
所有参数不会都变为0,因为还有后一项来平衡。
使用L2正则,每次都让参数变小一点,也叫做Weight Decay
正则化在深度学习的重要性不是很高,帮助往往没有特别显著,一个可能的原因是做了提前停止,我们可以决定什么时候停止训练,一般参数初始化都是一个很接近与0 的值,参数更新通常是离0越来越远,停止训练让参数更新次数变少,避免参数不会离0太远,正则化也是让参数不要离0太远,两者的作用就重叠了。

现在看L1正则
出现一个问题,绝对值不能微分怎么办?
绝对值的图形是V,那么在一边的微分是-1,另一边的微分是1,不能微分的地方只有值是0的点,那就不要管这个点。如果\(w\)是正的,微分就是1,负的微分就是-1。
参数更新的式子里\(-\eta \lambda sgn(w^t)\),\(w\)是正的,就减去一个值让参数变小,\(w\)是负的,就加上一个值让参数变大,不管参数是多少。跟L2对比,当参数>0时,两者作用都是让参数变小,但是L2是乘以一个值(0.99),而L1是减去一个固定值。如果参数为100万,L2里乘以0.99相当于100万减去一个很大的值,对L1来说是减去一个固定值。所以对L2来说,一个很大的参数,下降速度也会很快,但是对L1来说参数是大是小下降速度不会改变,通过L1还会有一些很大的参数值。
考虑很小的值,比如0.1、0.01这种接近于0,通过L2下降速度就很慢,那就会保留很多接近于0的值。而通过L1,每次下降固定值,就不会保留很多很小的值。所以L1后是稀疏的(有很多接近0的值,也有很多很大的值),L2平均都比较小。

人6岁的时候有很多的神经,14岁的时候神经变少了
加入正则化,因为权重是被动地接近0的,如果不去更新权重,就会变得越来越小,最后就不见了
dropout
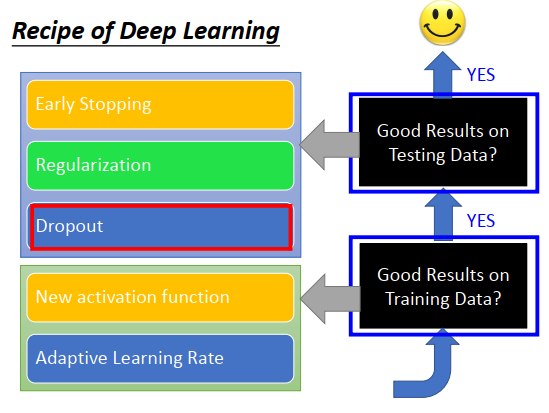
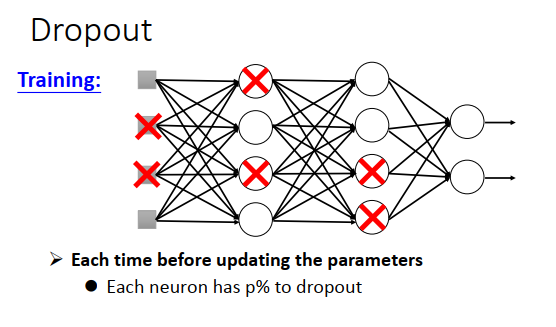
dropout是怎么做的?
train 中每次更新参数之前,对每一个神经元(包括输入层的每个元素)采样,每个神经元以概率p被丢弃。
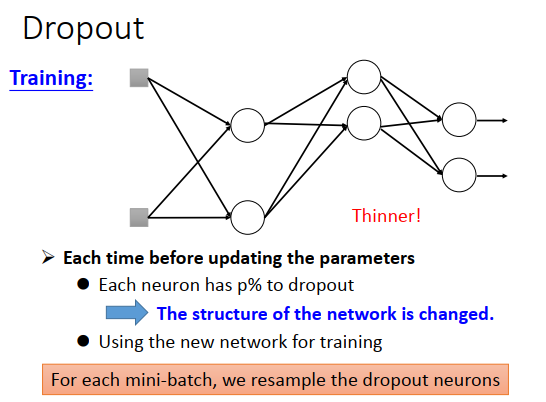
被丢弃的神经元连接的权重也丢弃。采样后网络结构就变得很细长。
注意dropout在每次参数更新之前都要重新做一遍,所以每次train 的网络结构都不一样
train 做dropout,train的结果是会变差的,但是test 结果会变好,所以不适合train 结果不好的网络调优
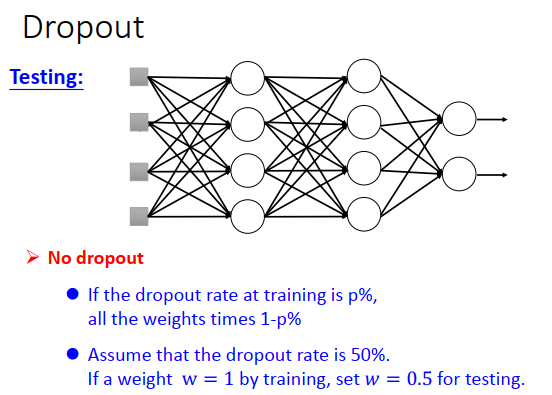
test 怎么做呢?
test的时候不做dropout,所有的神经元都要使用
假设train dropout rate是p%,那么在test的时候所有权重都要乘以\(1-p\%\)

为什么dropout有用?
直觉的想法:
train的时候会丢弃一些神经元,就像练功的时候脚上绑重物,实际战斗的时候重物拿下来就会变得很强
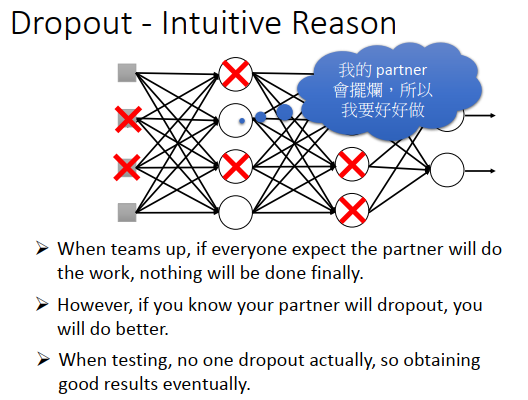
为什么dropout有用?
另外一个直觉的理由:
一个神经网络里的每个神经元都是一个学生,组在一起就是一个团队,团队里总有人会摆烂。
在train的时候假设队友会摆烂,test实际的时候每个人都在好好做,所以test结果更好
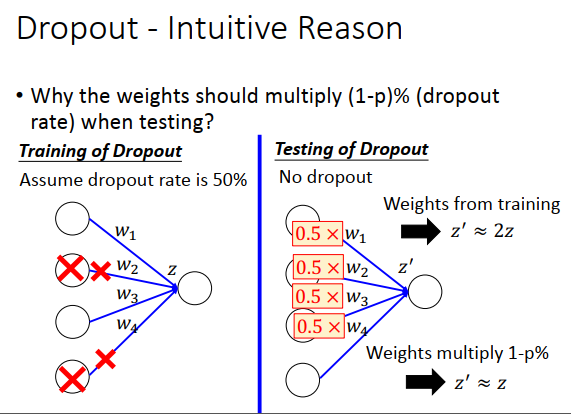
为什么train和test用的权重不一样?
直觉理由:
假设dropout rate 是50%,那么期望总是会丢掉一半的神经元,在test的时候 \(z\) 会变大两倍。所以在test的时候把权重都乘以0.5,做一下规范化,这时候z 就会约等于 train 的z
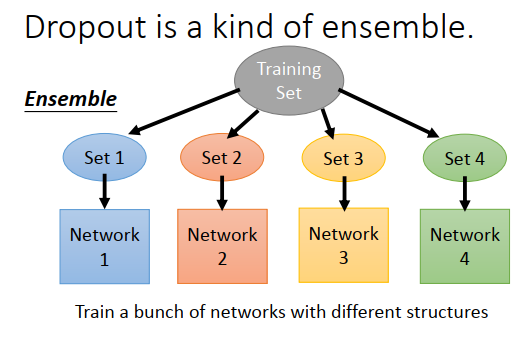
dropout有很多正式的解释
如果你有一个很复杂的model,往往是偏差小方差大,但是多个复杂model集成后方差会变小
dropout是一种终极的集成模型,每次训练都只是从训练集采样一部分,然后训练很多个model,每个model的结构都可以不一样
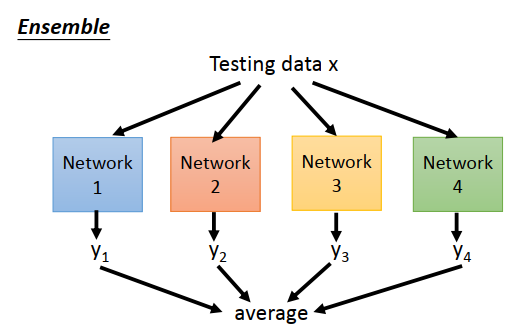
test的时候就相当于使用了很多个model,然后结果平均起来。
想想随机森林。
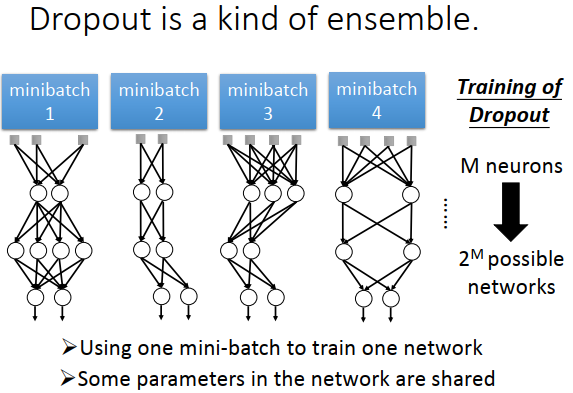
为什么说dropout是终极的集成模型?
每次更新参数之前,采样一个批次的数据,不同批次的网络不同。假设有M个神经元,每个神经元都可以丢弃或者不丢弃,所以可能的神经元批次有\(2^M\)种,总共有\(2^M\)种网络。例如一个神经网络使用100个数据,参数update几次,就有几个神经网络。
只使用100个数据训练,是否会有问题?
没有关系,因为不同的网络之间的参数是共享的,上图4个网络都有左下方的那个权重,那这个权重就是4个数据集合起来训练的结果。因为每次训练后,这个权重都被更新,只不过进行了4个批量梯度下降。
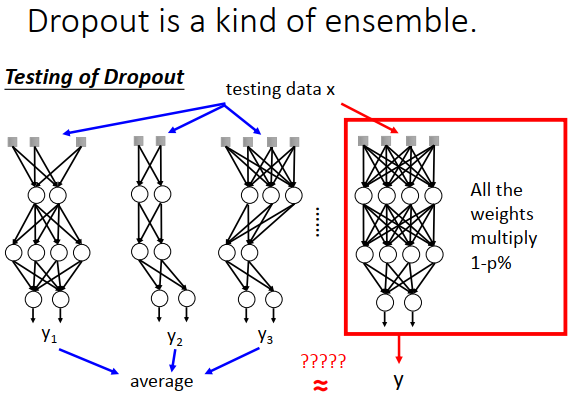
test怎么从集成的角度解释?
训练数据使用所有的神经网络模型,最后平均每个模型的输出,但是因为模型太多,运算会很慢。
而dropout认为只要把所有的权重乘以\(1-p\%\) ,由一个模型的输出约等于之前集成模型的平均值
为什么一个模型的输出约等于之前集成模型的平均值?
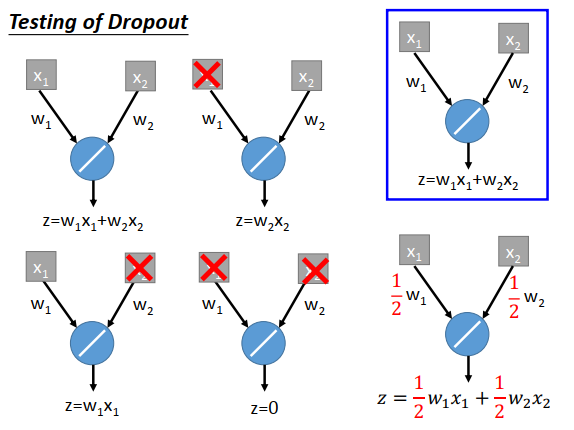
右上图所示,一个简单的神经元,激活函数是线性的,只有两个参数,不考虑偏差b
现在\(w_1,w_2\)是进过dropout训练后的参数值
做集成模型的话,理论上如上图左边所示,每个input可以被丢弃或不丢弃,那么总共有4种网络结构。
得到4个输出
\(z=w_1x_1+w_2x_2\)
\(z=w_2x_2\)
\(z=w_1x_1\)
\(z=0\)
4个输出平均后为\(\large z=\frac{1}{2}w_1x_1+\frac{1}{2}w_2x_2\),相当于对所有权重乘以1-p%不做集成的模型的输出
这里有趣的地方时只有激活函数为线性时才有以上结论,激活函数变为sigmoid或者其它非线性的函数,结果就不会相等了
也有个有趣的想法,就是如果激活函数使用的是接近于线性函数的比如ReLU和Maxout这种,那使用dropout效果就会比较好


 浙公网安备 33010602011771号
浙公网安备 33010602011771号