李宏毅深度学习笔记-深度学习简介

李宏毅深度学习笔记 https://datawhalechina.github.io/leeml-notes
李宏毅深度学习视频 https://www.bilibili.com/video/BV1JE411g7XF

step1 神经网络

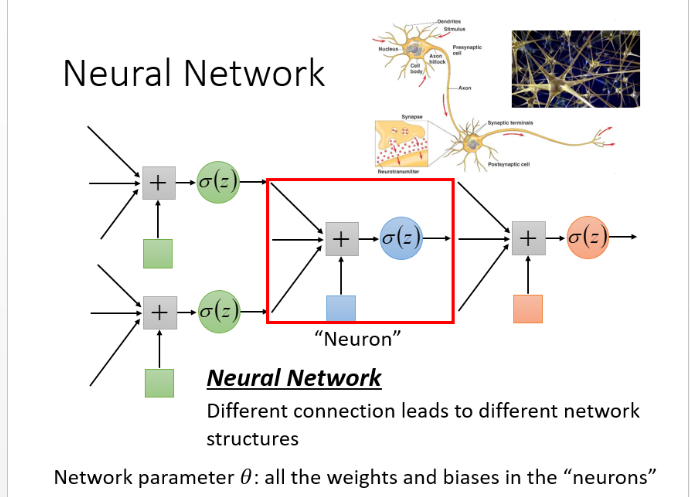
激活函数是sigmoid，红色圈是一组神经元，每个神经元都有自己的权重和偏差。

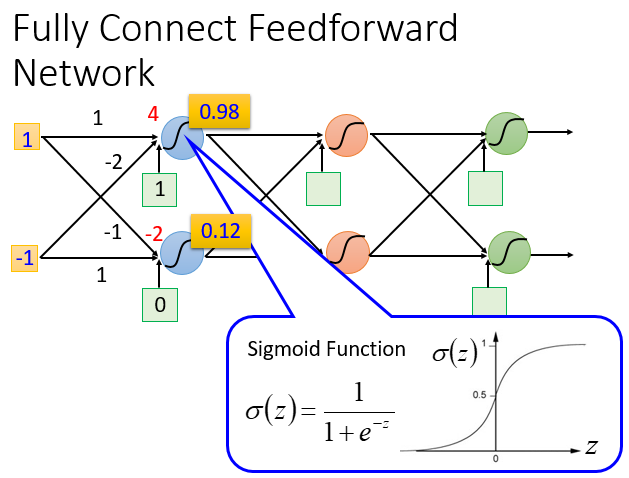
完全连接前馈神经网络

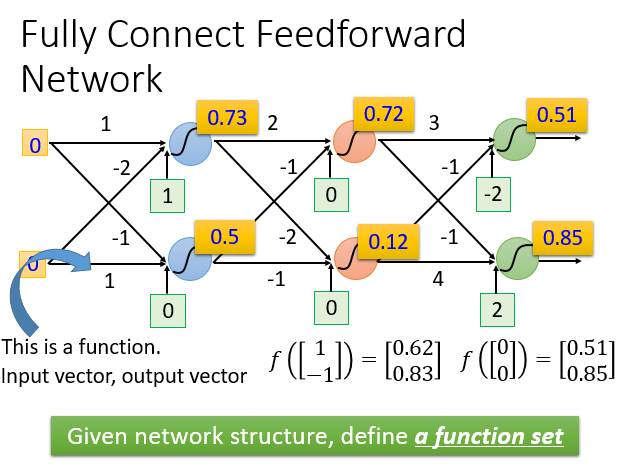
给定网络结构，相当于定义了一个函数集，每个神经元可以使用不同的函数，那么整个网络的函数集合是非常大，所以说深度学习可以拟合任意曲线。

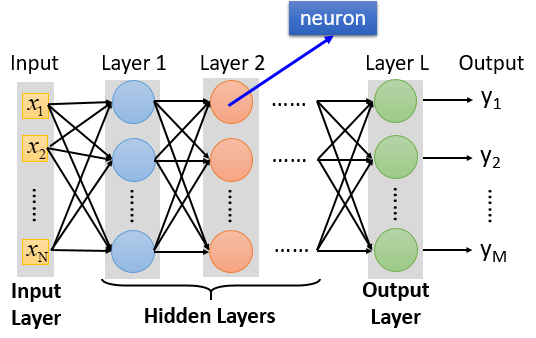
全链接：layer1与layer2之间两两都有连接

前馈：传递的方向是由后往前传

输入层不是有神经元组成的，严格讲不能当作一个layer

除了输入层和输出层，其他的叫做隐藏层，上图有L个隐藏层

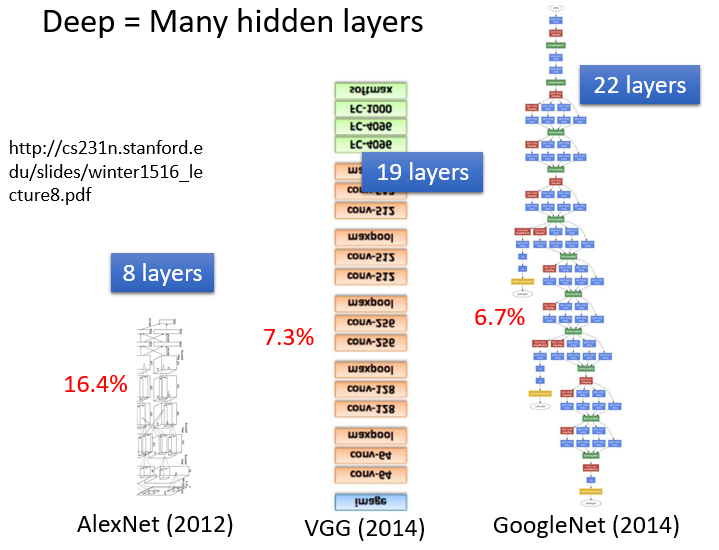
有很多个layer叫做deep,具体几个看个人

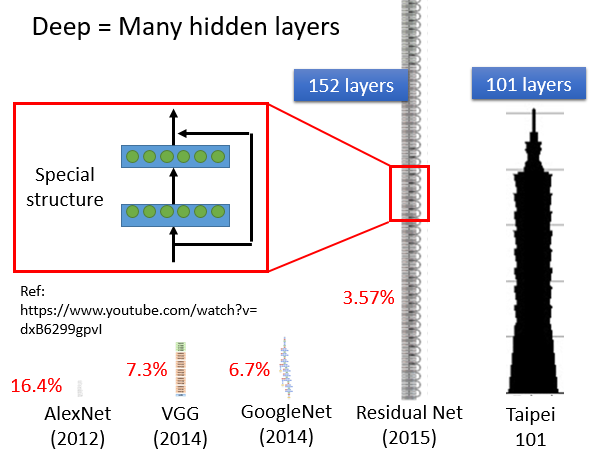
随着层数变多，错误率降低，随之运算量增大

矩阵计算

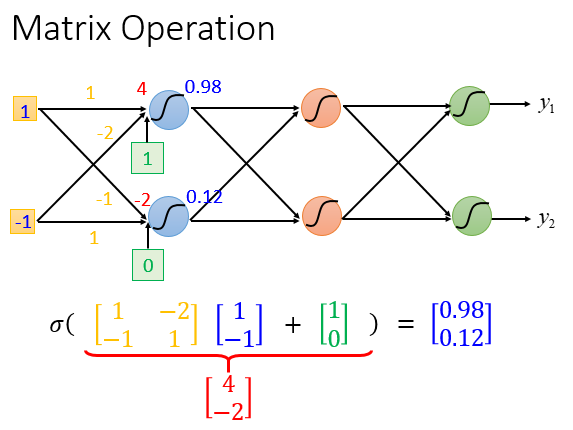
两个神经元的权重集合表示为\(\begin{bmatrix} 1 & -2 \\ -1 & 1 \end{bmatrix}\)

sigmoid的意义是激活函数，现在很少用sigmoid作为激活函数

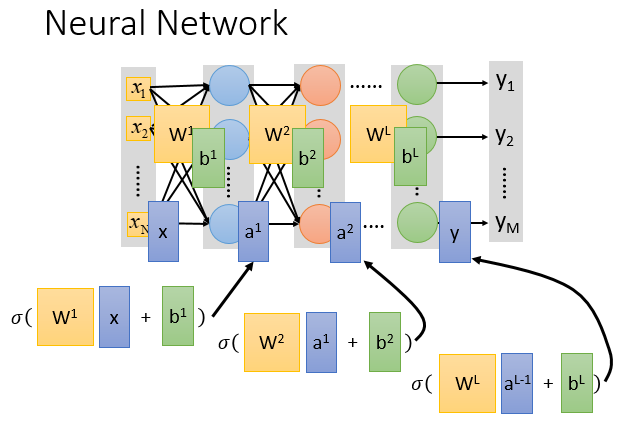
\(W^1=\begin{bmatrix} w_{11}^1&w_{21}^1& \cdots&w_{N1}^1 \\ w_{21}^1&w_{22}^1& \cdots&w_{N2}^1 \\ \vdots \\ w_{1N}^1&w_{2N}^1& \cdots&w_{NN}^1 \end{bmatrix}\)，\(x=\begin{bmatrix} x_1 \\x_2 \\ \vdots \\ x_N \end{bmatrix}\)，\(b^1=\begin{bmatrix} b_1^1\\b_2^1\\ \vdots \\ b_N^1\end{bmatrix}\)

整个神经网络运算就相当于一连串的矩阵运算

写成矩阵运算的好处是可以使用GPU加速

隐藏层-特征提取

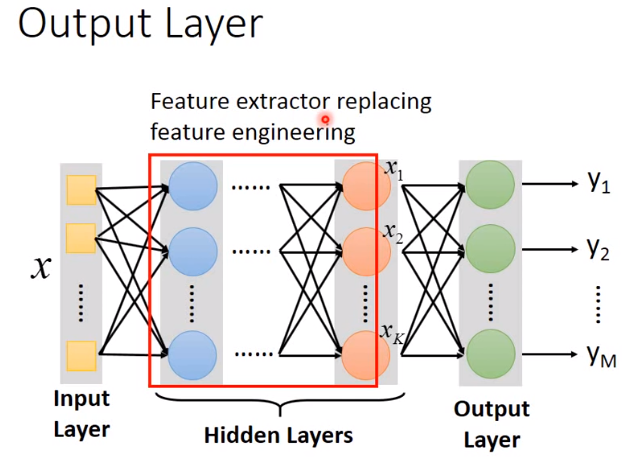
隐藏层看成是一个特征提取器，代替手动的特征工程

输出层的输入看成是\(x\)经过很多层复杂转换后，抽出的一组最好的feature，能用简单的分类器很好的分类

多分类的时候一般也是使用softmax函数

手写数字例子

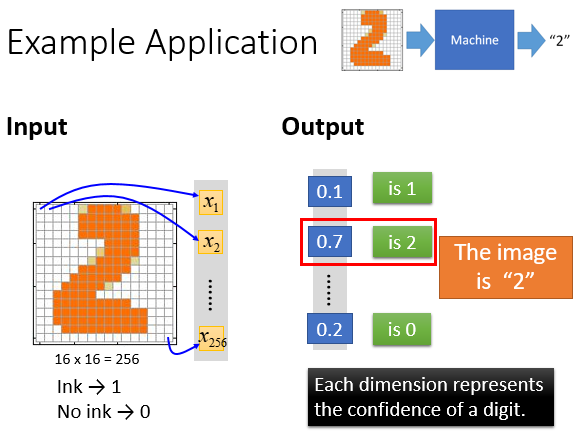
输入16*16=256维的向量

输出是对应是一个数字的概率

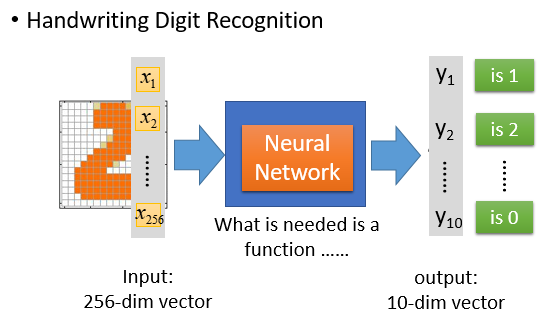
输入是256维的向量

输出是10维的向量

function就是一个神经网络

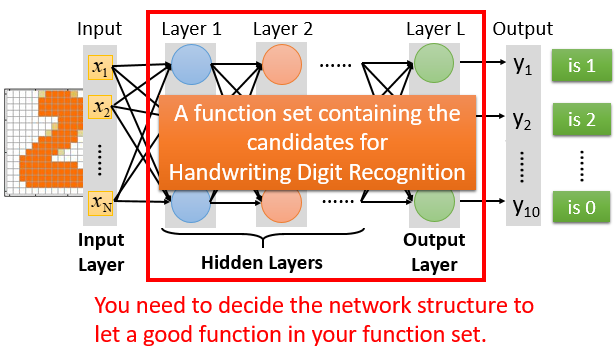
隐藏层是自己设计的，多少个layer,每个layer多少个神经元

结构决定了函数集，所以网络结构很关键

常用问题：

需要多少层隐藏层？每个隐藏层需要多少神经元？

只能凭着经验和直接，普通的机器学习要做好的特征工程，但是深度学习往往不需要做特征工程，但是需要设计好的网络结构。像语音识别，人很难知道怎么抽一组好的feature，因为不知道一组好的feature长什么样子，不如设计一个网络结构，或者尝试各种网络结构，让机器自己找出好的feature。

可以自动学习网络结构吗？

是可以的

可以自己设计网络结构吗？

可以的，比如不要fully connected ，神经元自己乱接。一种特殊的接法就是卷积神经网络。

step2 模型评估

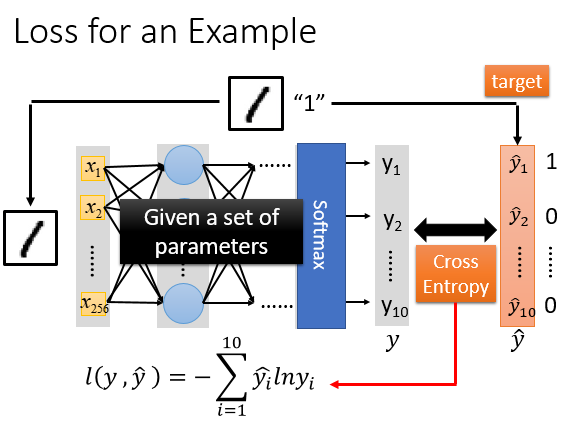
在神经网络中，如何决定一组参数的好坏？

有一张图片和label( \(\hat{y}\) )，input图片的pixel,通过神经网络得到一个output( y )，然后计算交叉熵，接下来调整参数最小化交叉熵

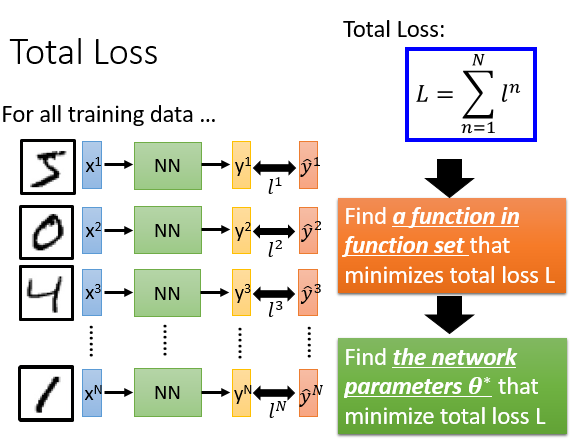
在整个training data里，定义总体损失，在function set 里找到一组function，或者找到一组神经网络的参数，最小化总体损失。

step3：选择最优函数

如何找到这组最优参数？

就是使用梯度下降法

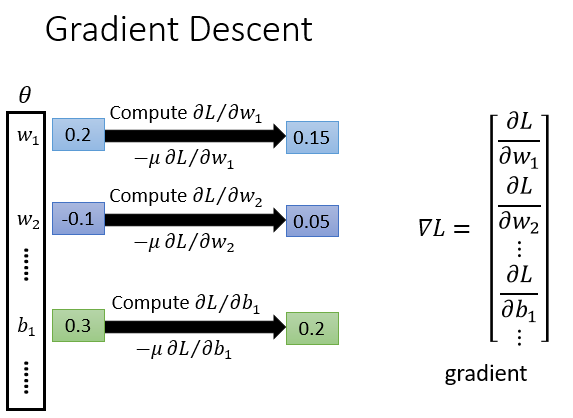
\(w_1\)是第一层隐藏层的所有参数

计算每个参数的偏微分，全部集合就是梯度，有了梯度后更新参数

反复计算梯度和更新参数