李宏毅深度学习笔记-Adagrad算法
李宏毅深度学习笔记 https://datawhalechina.github.io/leeml-notes
李宏毅深度学习视频 https://www.bilibili.com/video/BV1JE411g7XF
普通的梯度下降法

学习率\(\eta\)是个超参数需要人工调整,但是手工调整比较麻烦
普通方法可能出现的问题
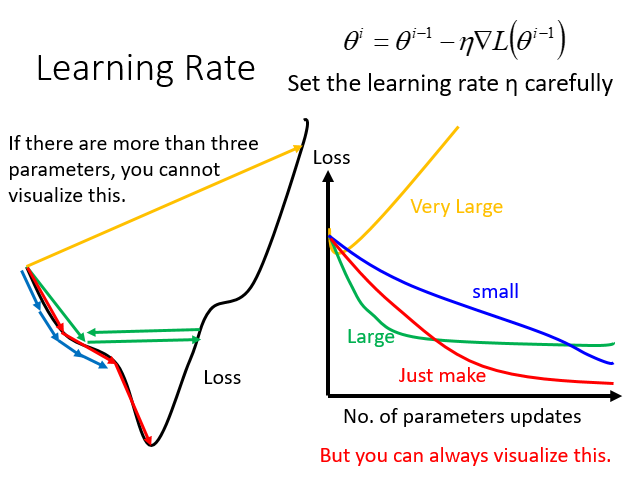
学习率太小(蓝色的线),下降慢,迭代次数多
学习率太大(绿色的线),下降快,但是太快容易在极优值附近振荡
学习率特别大(黄色的线),直接越过了极优值
如何改善可能出现的问题
想法:随着迭代次数增加,让学习率变小
- 初始迭代时,使用较大的学习率加速下降
- 迭代几次后,减小学习率防止振荡和越过
可以使用式子:\(\large \eta^t=\frac{\eta}{\sqrt{t+1}}\),\(t\)增加,\(\eta^t\)减小
当然,对每个参数都要使用不同的学习率,这样效果会更好,AdaGrad是这种思想的一种简单算法
AdaGrad算法

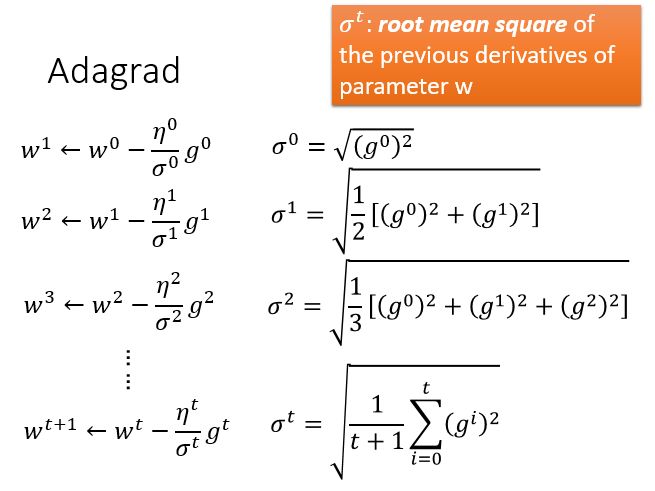
每个参数的学习率都把它除上之前微分的均方根,\(\sigma^t\)是每个参数的所有偏微分的均方根
举个例子:
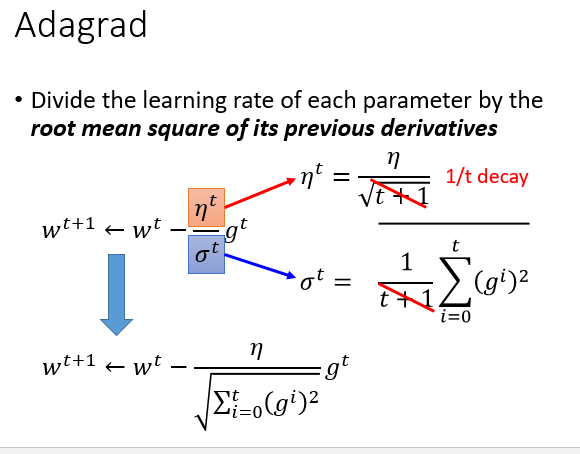
Adagrad 式子可化简(都有\(\sqrt{t+1}\))
Adagrad 里的问题
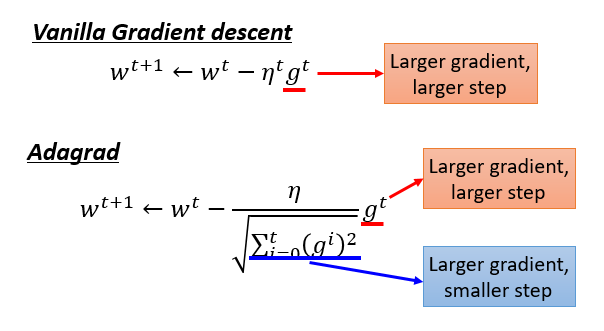
Adagrad 中,梯度越大,说明步伐越大,但分母里梯度越大,又说明步伐越小,这里不是会有矛盾吗?
直观解释

分子变大,分母变小,那分子式变化程度很大,造成反差的效果
正式的解释
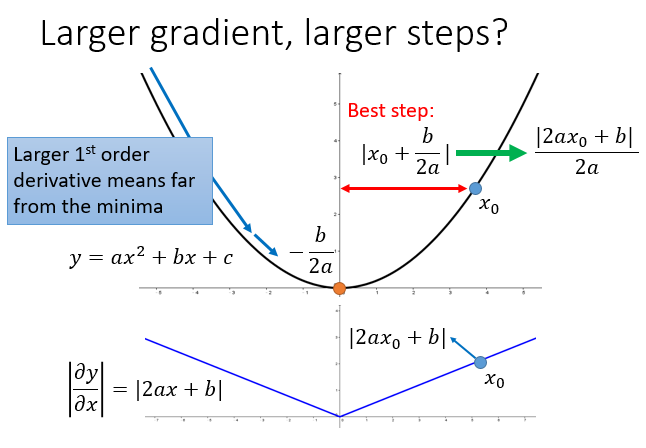
\(\large -\frac{b}{2a}\)不是等于0,这里只是说明是一个最小值点,对\(x\)求微分,那么只有\(x\)在变动
初始点\(x\)坐标为\(x_0\)时,最佳的变动范围是\(x_0\)到最低点的距离\(|x_0+\frac{b}{2a}|\) (注意是\(x\)轴上的变动),可以写成\(\large |\frac{2ax_0+b}{2a}|\) ,刚好\(|2ax_0+b|\) 是微分在初始点的绝对值。如果步伐和微分成正比,那么这个步伐就比较好。
画图说明下,为什么是横轴上的距离
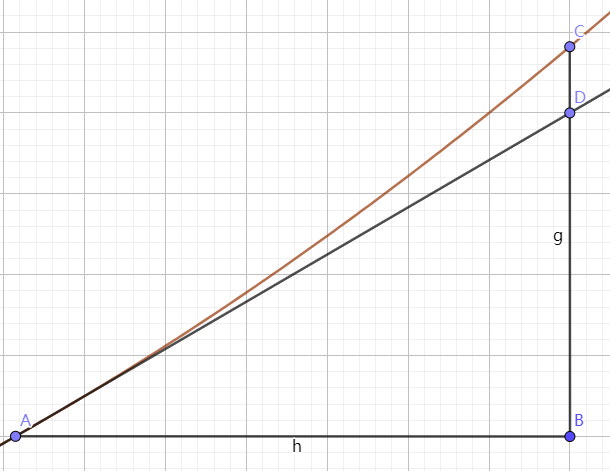
A点斜率是\(\frac{BD}{AB}\), A点微分为\(\lim \limits_{AB\rightarrow0}\frac{CB}{AB}\),梯度其实是和\(\Delta x\)反向的,因为只有一个参数\(x\),所以\(\Delta x\)就是\(AB\),那么其实梯度的方向是在\(x\)轴上的
以上说明梯度越大,点离最低点越远
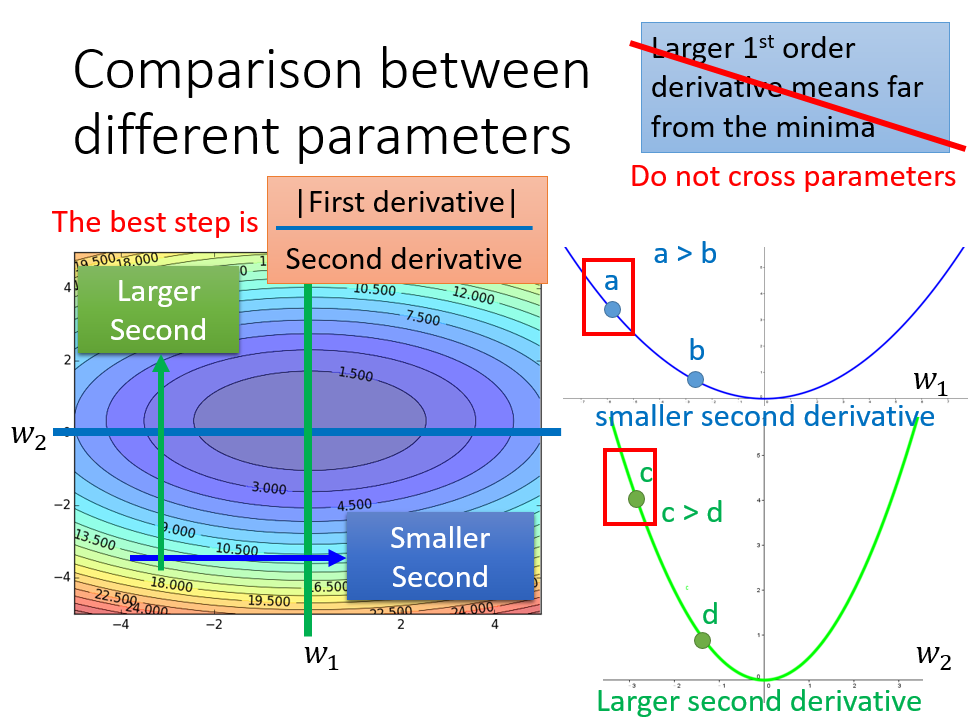
梯度越大,点离最低点越远在多参数上是不成立的
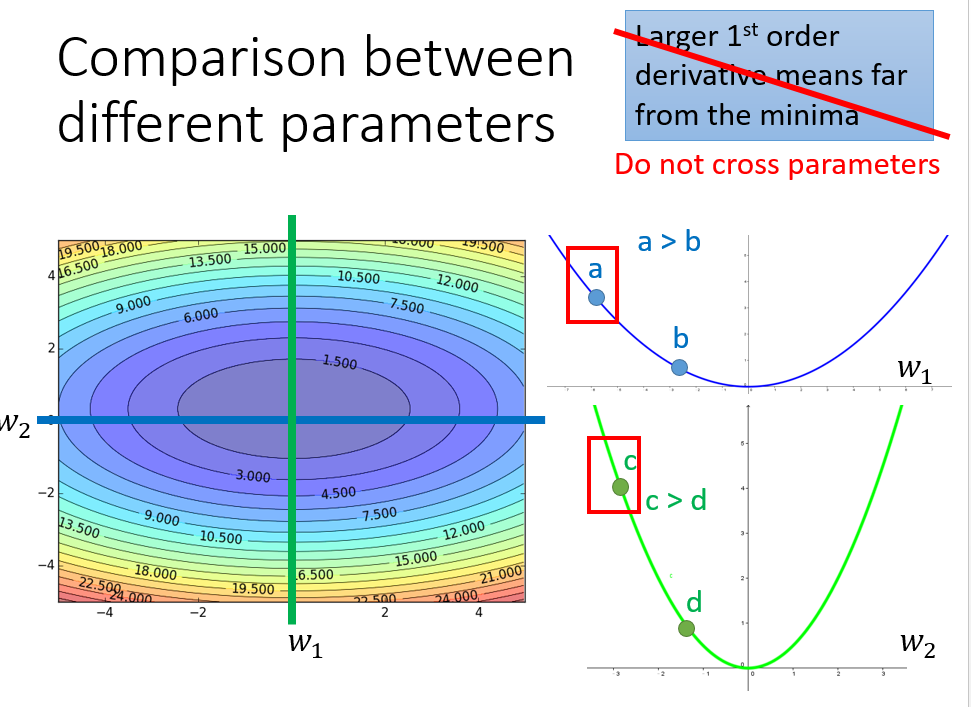
只考虑参数 \(w_1\),是图中蓝色的线;只考虑参数 \(w_2\),就像图中绿色的线
\(c\)点梯度比\(a\)大,但是\(c\)距离最低点更近
其实最佳距离中还有个分母\(2a\),是\(y\)的二次微分
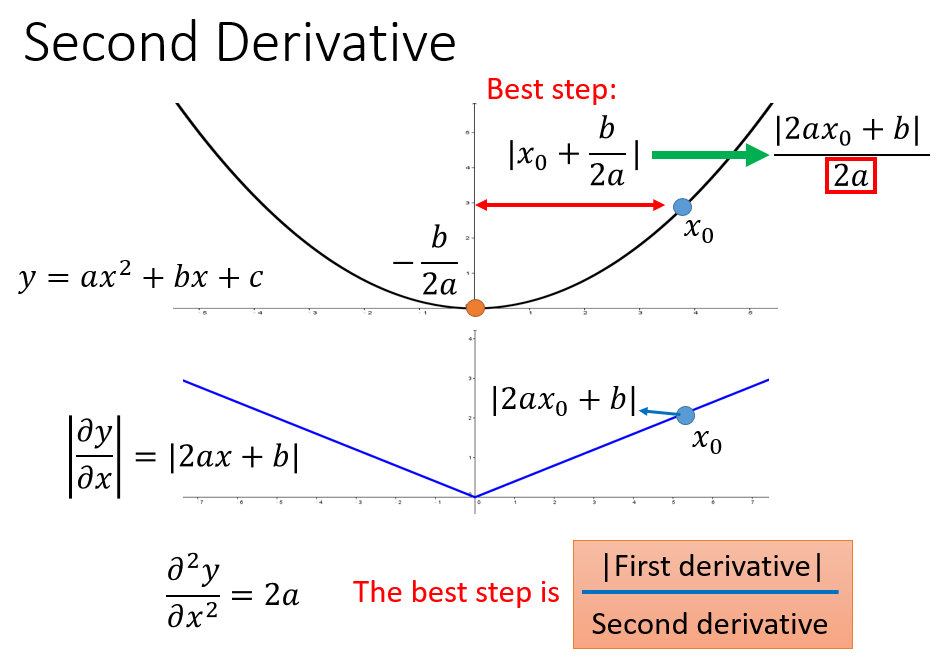
那么最好的step就要考虑二次微分
进一步回到Adagrad
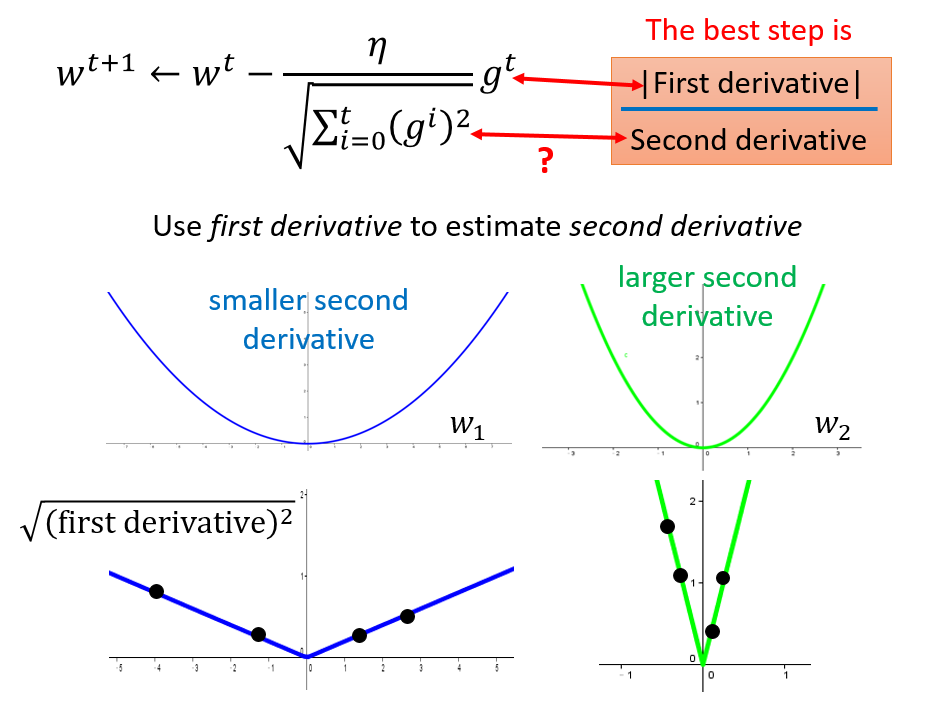
分母\(\sqrt{\sum\limits_{i=0}^t (g^i)^2}\) 是在模拟二次微分,因为计算二次微分在实际问题中是开销很大的


