Learning under Concept Drift: A Review 概念漂移综述论文阅读

首先这是2018年一篇关于概念漂移综述的论文^[1]。

最新的研究内容包括

　（1）在非结构化和噪声数据集中怎么准确的检测概念漂移。how to accurately detect concept drift in unstructured and noisy datasets

　（2）怎么用一种可解释的方法来定量理解概念漂移。how to quantitatively understand concept drift in a explainable way

　（3）如何有效的结合相关知识和概念漂移。how to effectively react to drift by adapting related knowledge

该论文做了：

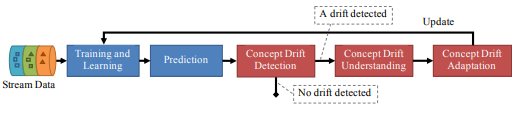
　（1）总结了概念漂移的研究成果，将概念漂移研究分为三类:概念漂移检测、概念漂移理解和概念漂移适应，为概念漂移研究的发展提供了清晰的框架。

　（2）提出了一种新的概念漂移理解方法，用于从时间、方式和地点三个方面检索概念漂移的状态信息。

　（3）揭示了概念漂移下的主动学习技术和基于模糊能力模型的漂移检测技术，并对涉及到概念漂移的相关研究进行了综述。

　（4）系统地检查两套概念漂移数据集，合成数据集和真实数据集，通过多个维度:数据集描述，可用性，漂移类型的适用性，和现有的应用程序。

　（5）提出了该领域的几个新的研究课题和潜在的研究方向。

论文中图 

 

概念漂移的定义：

　给定一个时间范围[0, t]，样本表示为S_0,t ={d₀, . . . , d_t}，其中d_i = (X_i , y_i)是对于概念的一次观察，Xi是特征向量，y是标签，S_0,t服从一个确定分布F_0,t(X, y).

　如果F_0,t(X, y) ≠ F_t+1,∞(X, y),则称概念漂移发生在t+1时刻，记为 ∃t: P_t(X, y) 6 ≠ P_t+1(X, y)

 

　Concept drift 也有一些人称之为 dataset shift [2] or concept shift [3].[4]认为Concept drift  or shift 只是 dataset shift 的子类，它认为dataset shift 包括 covariance shift，prior probablity shift and concept shift.

　联合概率函数 P_t(X, y) 可以解构为  P_t(X, y) = P_t(X) × P_t(y|X)，因此概念漂移可以由三个源引起

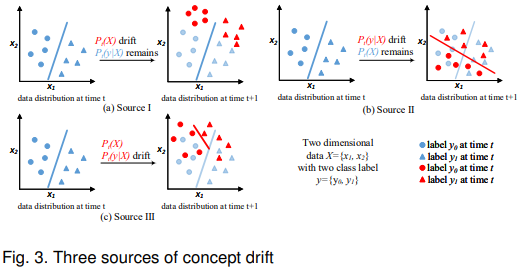
　　1）P_t(X) ≠ P_t+1(X) while P_t(y|X) = P_t+1(y|X), that is, 关注 P_t(X)上的漂移 而 P_t(y|X) 保持不变.  P_t(X) 的漂移不影响决策边界, 因此也被认为是一种虚漂移  virtual drift[5], Fig. 3(a).

　　2）P_t(y|X) ≠ P_t+1(y|X) while P_t(X) = P_t+1(X) while P_t(X) remains unchanged. 这种漂移会使决策边界变化，从而导致预测精度下降, 也被称为实漂移 actual drift, Fig. 3(b).

　　3）结合了上面两者, Pt(X) ≠ Pt+1(X) and Pt(y|X) ≠ Pt+1(y|X).两者都发生了漂移, 因为这两种变化都传达了关于学习环境的重要信息 Fig. 3(c).

 

　通常，概念漂移方式分为四类： 突发式漂移， 渐进式漂移， 增量式漂移， 复发式漂移

 

 

 

 

漂移检测

　漂移检测的一般框架

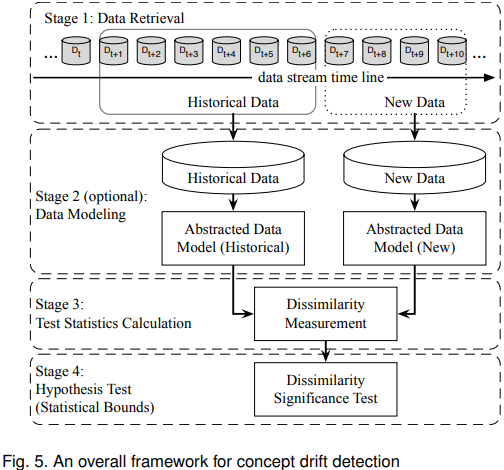
　　General 框架一般分为4个阶段，

　　　Stage 1：数据获取。由于单个数据实例不能携带足够的信息来推断整个分布，所以知道如何组织数据块形成有意义的模式或知识在数据流分析任务中是很重要的。

　　　Stage 2：数据建模。抽象出数据的特征，漂移的特征对系统的影响最大。这个阶段是可选的，因为它主要关注维数减少，或样本大小减少，以满足存储和速度的要求。

　　　Stage 3： 统计值计算。是衡量不一致性，或者漂移量。通过统计测试和假设检验来定量研究漂移的严重性。. 不相似度度量还可以用于聚类评价，并确定样本集之间的不相似度。

　　　Stage 4：使用特定的假设检验来评估阶段3中观察到的变化的统计显著性，或p值。即这种变化由概念漂移而非噪声或随机样本选择偏差[3]引起的可能性有多大。最常用的假设检验有:最常用的假设检验有:估计检验统计量的分布[5]，[6]， bootstrapping[7]，[8]，排列检验[9]。

 

 

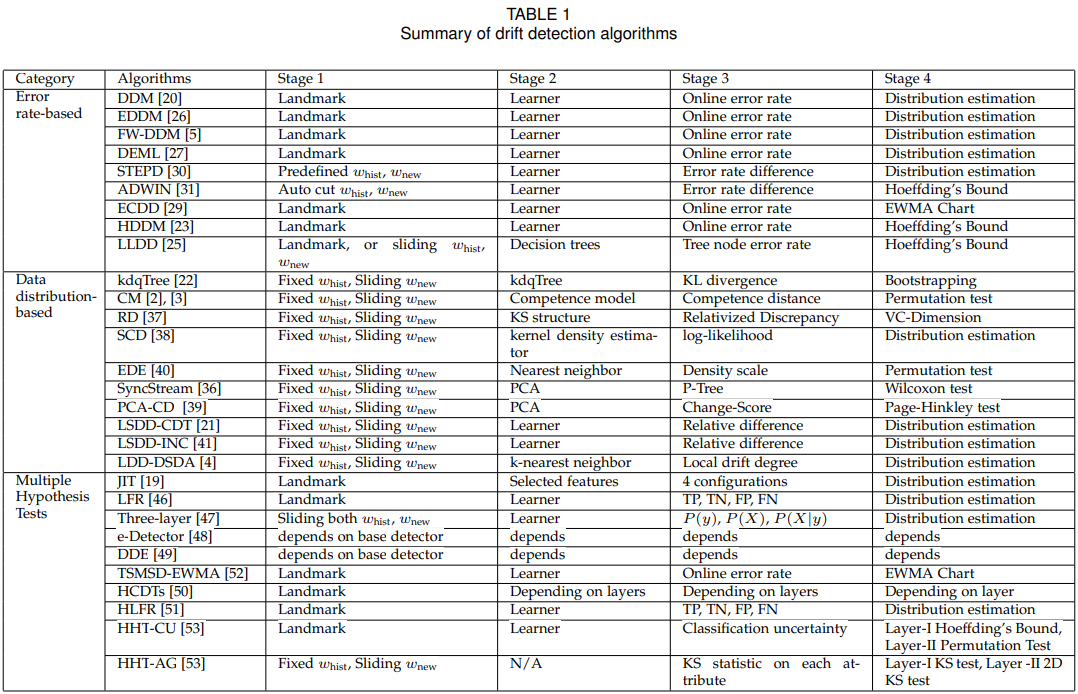
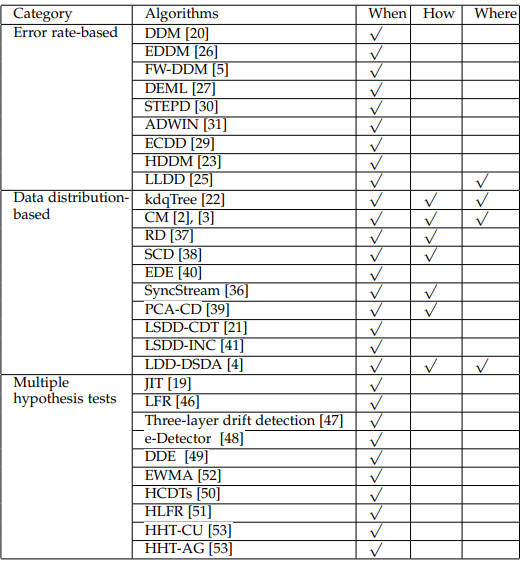
　概念漂移检测算法

　　Error rate-based drift detection

　　　基于错误率来检测，具体来说对于在线检测，就是分类错误显著升高，或者显著降低，这时将触发漂移检测。

　　　Drift Detection Method (DDM) [20] 是被引最多的一种漂移探测方法之一，这是第一个定义预警级别和漂移级别的概念漂移检测算法。

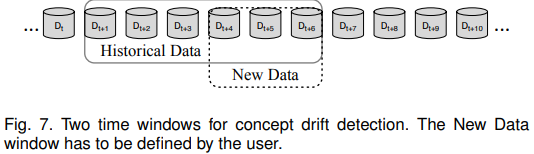
　　　　Stage 1 通过时间窗实现，如图6所示。当一个新的数据实例可以用于评估时，DDM会检测时间窗口内的总体在线错误率是否显著增加。当错误率变化的置信度达到预警级别时，DDM开始构建一个新的学习器，同时使用旧的学习者进行预测。如果变化达到漂移级别，旧的学习者将被新的学习者代替，进行进一步的预测任务。为了获得在线错误率，DDM需要一个分类器来进行预测。这个过程将训练数据转换为学习模型，这是第二阶段(数据建模)。阶段3的测试统计数据构成在线错误率。假设检验阶段(第四阶段)通过估计在线错误率的分布，计算预警级别和漂移阈值进行假设检验。

 

 

 

　　　类似的还有LLDD [10], EDDM [11], HDDM [12], FW-DDM [13], DELM[14]。

　　　LLDD修改了3,4阶段，将整个漂移检测问题分解为一组基于决策树节点的漂移检测问题。

　　　EDDM利用两个正确分类间的距离改进了DDM的第3阶段，提高了漂移检测的灵敏度。

　　　HDDM 修改阶段4，使用了Hoeffding不等式识别漂移临界区域的方法。

　　　FW-DDM改进了DDM的第一阶段，使用模糊时间窗代替传统的时间窗来解决逐步漂移问题。

　　　DEML没有改变DDM检测算法，而是采用了一种新的基学习器，它是一种单隐层反馈神经网络，称为 ELM [15]，以改进漂移确定后的自适应过程。

　　　ECDD[16] 使用EWMA图表来跟踪错误率的变化。用动态均值替代静态均值，动态方差为，其中λ是新数据对比旧数据的权重，作者建议取0.2.

 

 

当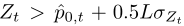时,ECDD将会发出预警，当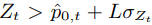，这时就认为发了概念漂移。

 

 

　　　与DDM等类似算法相比，STEPD[17]，比较最近的时间窗口和整个时间窗口来检测错误率的变化

　　　ADWIN不需要指定时间窗口大小，需要指定一个足够大的窗口总大小。对所有子窗口计算漂移量。

 

 

 

 

　　Data Distribution-based Drift Detection

　　　基于数据分布差异的漂移检测，通过计算数据分布的差异度，来进行检测，不仅可以检查时间维度上的漂移，也可以检测数据集内部的概念差异。然而这些算法的资源消耗通常比上者要高。通常的做法是利用两个滑动窗口来选取数据。

　　　最初使用这种想法的是[18]，如果分布有它自己的概率密度函数，则距离可以计算为。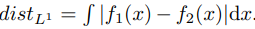

 

 

　　　类似的还有ITA[8]，它使用kdqTree来划分 历史数据和 新数据， 然后用KL散度来计算差异性。ITA采用的假设检验方法是将W_hist、W_new合并为W_all，重采样为W_hist、W_new进行bootstrapping，则确定概念漂移，其中α是控制漂移检测灵敏度的显著水平。

　　　类似的算法还有SCD[19]，n CM[20]，PCA-CD [21]，EDE[22]，LSDD-CDT[21]，LSDD-INC[23]，LDD-DSDA[24]。

 

　　Multiple Hypothesis Test Drift Detection

    　　　　

 

 

 

 

 

 　　　并行假设检验

　　　　最早的算法是JIT[5]，核心思想是拓展CUSUM test，作者给出了给出了漂移检测目标的4种配置方案，1）PCA提取后的特征，移除和小于某一阈值的情况。 2）PCA提取的特征，加上一些原始特征中的通用特征。 3）对每一个特征独立检测。4）检测所有可能组合的特征空间。

　　　　相似的LFR[25]，考察TP, TN, FP, FN的变化，而不是准确率的变化。

　　　　IV-Jac[26]是一种三层检测算法，第一层检测标签层面，第二层是特征层面，第三层决策边界层面。它通过提取 证据权重 WoE，和信息价值 IV，来观察其变化。

　　　串行假设检验

　　　　HCDTs[27]最先设计了 检测层 和 验证层，验证层根据检测层的返回结果决定激活或者休眠，给了两个设计验证层的策略，1）通过最大相似度来计算测试层数据的分布， 2）调整一种已有的假设检验方案。

　　　　HLFR[28]类似的，使用LFR作为检测层，把验证层简单的使用 0-1损失函数进行评估，超过阈值则为发生概念漂移。

 

 

 

漂移理解

属于作者自己的新增部分，要解决概念漂移，要从时间上何时发生，地点上哪些特征or标签，程度上的严重性来考量。内容比较冗余。

 

 

 

 

 

 

漂移调整

　发生概念漂移后，如何调整我们的算法才是最重要的。有三种主要的调整方案，应对不同的形式的概念漂移。

　Training new models for global drift

　　最简单有效的方法就是训练一个新的学习器。窗口策略通常会被使用。Paired Learners[fdfd]就是这种。

　　关于窗口策略，对于窗口的大小，小窗口可以反映最新的数据，大窗口可以为模型提供更多训练数据。ADWIN不需要固定窗口尺寸，根据两个子窗口之间的变化率计算最佳子窗口大小。找到最优窗口割后，删除包含旧数据的窗口，用最新的窗口数据训练新模型。

　　DELM没有使用全部重新训练的策略，而是当错误率上升时，为提高其逼近能力加入更多节点，继续训练。

　　FP-ELM[29]是一种elm扩展方法，它通过引入遗忘参数来适应漂移树模型。

　　OS-ELM[30]是另一种抑制因子模型的在线集成，它使用有序聚合(OA)技术集成ELM，克服了确定最优集成大小的问题。

　　采用基于能力模型的漂移检测算法[9]定位案例库中的漂移实例，并将其与噪声实例区分开，采用冗余去除算法， 逐步冗余消除(Stepwise Redundancy Removal, SRR)，以统一的方式去除冗余实例，保证减少的案例库仍能保留足够的信息用于未来的漂移检测。

　Model ensemble for recurring drift

　　对于recurring drift 复发式漂移，保留和重用旧的模型可以节省很大时间。 这是使用集成学习解决问题的核心思路。

 

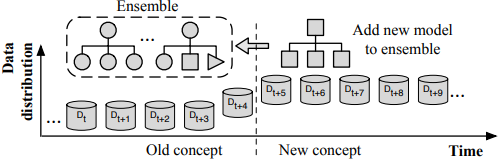
　　ARF[31]算法，它在随机森林树算法的基础上引入了概念漂移检测方法，如ADWIN，以决定何时用新树替换旧树。

 

　　DWM[32]就是这样一种集成方法，它可以通过一组简单的加权投票规则来适应漂移。它根据单个分类器和全局集成器的性能来管理基分类器。如果集成误分类了一个实例，DWM将训练一个新的基分类器并将其添加到集成中。如果基本分类器错误地分类了实例，DWM会减少它的权重一个因子。当基分类器的权重低于用户定义的阈值时，DWM将其从集合中移除。这种方法的缺点是，添加分类器过程可能被触发得太频繁。

　　一个著名的集合法，Learn++NSE[33]，通过根据基分类器对最新一批数据的预测错误率加权来缓解这个问题。如果最小分类器的错误率超过50%，将根据最新的数据训练一个新的分类器。

　　AUE2[34]的提出重点在于同时处理突发式漂移和渐变式漂移。它是一种基于增量基分类器的批处理加权投票集成方法。通过重新加权，整个系统能够对突然漂移做出快速反应。所有的分类器也用最新的数据增量地训练，这确保了总体的演进与渐进的漂移。

　　OWA[35]通过为不同的概念漂移类型使用加权实例和加权分类器来构建集合，实现了相同的目标。

　Adjusting existing models for regional drift

　　当漂移只发生在局部地区时，这类方法中的许多方法是基于决策树算法的，因为树有能力分别检查和适应每个子区域。

　　VFDF[36] 针对高速数据流的在线决策树算法。它使用Hoeffding边界来限制节点分割所需的实例数量。它有许多优点 1）只需处理数据一次，不需要存储。2）树本身只占很小的空间。3）维护树的成本很低。

　　CVFDT[37]，保持一个滑动窗口来保存最新的数据。在窗口的基础上训练备选子树，并对其性能进行监控。如果备选子树的表现优于原来的对应子树，它将被用于未来的预测，而原来废弃的子树将被修剪。

　　VFDTc[38]是对VFDT进行改进的另一个尝试，它增强了一些功能:处理数字属性的能力;朴素贝叶斯分类器在树叶分类中的应用以及对概念漂移的检测和适应能力。提出了两种节点级漂移检测方法。第一种方法使用分类错误率，第二种方法直接检查分布差异。

　　[39], [40]进一步扩展了VFDTc，使用自适应叶策略，从多数投票、朴素贝叶斯和加权朴素贝叶斯这三个选项中选择最佳分类器

　　尽管VFDT取得了成功，但最近的研究[41]、[42]表明，它的基础Hoeffding界可能不适用于节点分裂计算，因为它计算的变量，即信息增益，不是独立的。

 

评估与数据集

　对于能够处理概念漂移的学习算法的评估，有三个独特的流程

　　1) holdout, 2) prequential, and 3) controlled permutation

　　1）holdout应该遵循这样的规则:当测试一个学习算法在时刻t时，holdout集代表的是在时刻t时完全相同的概念。不幸的是，它只适用于具有预定义的概念漂移时间的合成数据集。

　　2）Prequential是流数据中常用的一种评估方案。每个数据实例首先用来测试学习算法，然后训练学习算法。该方案的优点是不需要知道概念的漂移时间，最大限度地利用了现有数据。 误差是根据预测和观测标签之间的损失函数的累加和计算的。错误率估计有三种:里程碑窗口、滑动窗口和遗忘机制。

　　3）Controlled permutation运行多个测试数据集，其中数据顺序以一种可控的方式进行了排列，以保持局部分布，这意味着最初在时间上彼此接近的数据实例在一次排列之后需要保持接近。受控制的排列减少了其先行评估对序列中固定顺序的数据产生偏差结果的风险。

　对涉及概念漂移的数据集的评价指标可以从传统的精度度量中选择，如检索任务中的精度/召回率、回归中的平均绝对缩放误差、推荐系统中的均方根误差等。

　除此以外，作者还推荐可以使用以下几点度量：

　　1）RAM-hours [43] 用于计算数据挖掘的成本。

　　2）Kappa statistic 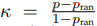[44]， 考虑不平衡分类时使用，p是分类器的准确率，P_ran是随机分类器的准确率

　　3）Kappa-Temporal statistic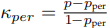[45] 考虑时序的分类使用，

 

 

　　4)  Combined Kappa statistic [45] 综合上面两者的使用。

 

 

　　5) Prequential AUC [46]

　　6) 平均归一化面积(NAUC)值[47]，用于概念漂移的流数据分类。

　对于显著性的度量，有以下三种流行方案：

　　1）McNemar test

　　2）Sign test

　　3）Wilcoxon’s signrank tes

 

　合成数据集

 

 

 

 

 

 

 

 

 

 

 

 

 

 

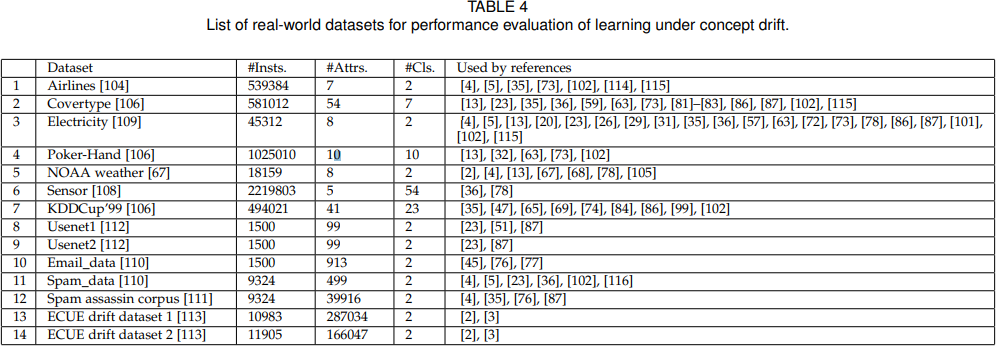
　真实世界的数据集

 

 

 

此文是本人对Learning under Concept Drift: A Review的论文阅读记录，感谢Jie Lu, Anjin Liu, Fan Dong, Feng Gu, Joao Gama, and Guangquan Zhang等人的付出。

第一次写论文“读后感”，见谅见谅。如有侵权，请告之删除。

 

 

[1] Learning under Concept Drift: A Review.

[2] G. Widmer and M. Kubat, “Learning in the presence of concept drift and hidden contexts,” Machine Learning, vol. 23, no. 1, pp. 69–101, 1996.

[3] S. Amos, “When training and test sets are different: characterizing learn.

[4] J. G. Moreno-Torres, T. Raeder, R. Alaiz-Rodr´ıguez, N. V. Chawla, and F. Herrera, “A unifying view on dataset shift in classification,” Pattern Recognit., vol. 45, no. 1, pp. 521–530, 2012.

[5] C. Alippi and M. Roveri, “Just-in-time adaptive classifiers part i: Detecting nonstationary changes,” IEEE Trans. Neural Networks, vol. 19, no. 7, pp. 1145–1153, 2008.

[6] J. Gama, P. Medas, G. Castillo, and P. Rodrigues, “Learning with drift detection,” in Proc. 17th Brazilian Symp. Artificial Intelligence, ser. Lecture Notes in Computer Science. Springer, 2004, Book Section, pp. 286–295.

[7] L. Bu, C. Alippi, and D. Zhao, “A pdf-free change detection test based on density difference estimation,” IEEE Trans. Neural Networks Learn. Syst., vol. PP, no. 99, pp. 1–11, 2016.

[8] T. Dasu, S. Krishnan, S. Venkatasubramanian, and K. Yi, “An information-theoretic approach to detecting changes in multidimensional data streams,” in Proc. Symp. the Interface of Statistics, Computing Science, and Applications. Citeseer, 2006, Conference Proceedings, pp. 1–24.

[9] N. Lu, G. Zhang, and J. Lu, “Concept drift detection via competence models,” Artif. Intell., vol. 209, pp. 11–28, 2014.

[10] J. Gama and G. Castillo, “Learning with local drift detection,” in Proc. 2nd Int. Conf. Advanced Data Mining and Applications. Springer, 2006, Conference Proceedings, pp. 42–55.

[11] M. Baena-Garc´ıa, J. del Campo-Avila, R. Fidalgo, A. Bifet, ´ R. Gavalda, and R. Morales-Bueno, “Early drift detection ` method,” in Proc. 4th Int. Workshop Knowledge Discovery from Data Streams, 2006, Conference Paper.

[12] I. Frias-Blanco, J. d. Campo-Avila, G. Ramos-Jimenez, R. MoralesBueno, A. Ortiz-Diaz, and Y. Caballero-Mota, “Online and non-parametric drift detection methods based on hoeffding’s bounds,” IEEE Trans. Knowl. Data Eng., vol. 27, no. 3, pp. 810– 823, 2015.

[13] A. Liu, G. Zhang, and J. Lu, “Fuzzy time windowing for gradual concept drift adaptation,” in Proc. 26th IEEE Int. Conf. Fuzzy Systems. IEEE, 2017, Conference Proceedings.

[14] S. Xu and J. Wang, “Dynamic extreme learning machine for data stream classification,” Neurocomputing, vol. 238, pp. 433–449, 2017.

[15] G.-B. Huang, Q.-Y. Zhu, and C.-K. Siew, “Extreme learning machine: Theory and applications,” Neurocomputing, vol. 70, no. 1–3, pp. 489–501, 2006

[16] G. J. Ross, N. M. Adams, D. K. Tasoulis, and D. J. Hand, “Exponentially weighted moving average charts for detecting concept drift,” Pattern Recognit. Lett., vol. 33, no. 2, pp. 191–198, 2012.

[17] K. Nishida and K. Yamauchi, “Detecting concept drift using statistical testing,” in Proc. 10th Int. Conf. Discovery Science, V. Corruble, M. Takeda, and E. Suzuki, Eds. Berlin, Heidelberg: Springer Berlin Heidelberg, 2007, Conference Proceedings, pp. 264–269.

[18] D. Kifer, S. Ben-David, and J. Gehrke, “Detecting change in data streams,” in Proc. 30th Int. Conf. Very Large Databases, vol. 30. VLDB Endowment, 2004, Conference Proceedings, pp. 180–191. 

[19] X. Song, M. Wu, C. Jermaine, and S. Ranka, “Statistical change detection for multi-dimensional data,” in Proc. 13th ACM SIGKDD Int. Conf. Knowledge Discovery and Data Mining. San Jose, California, USA: ACM, 2007, Conference Paper, pp. 667–676.

[20] N. Lu, J. Lu, G. Zhang, and R. Lopez de Mantaras, “A concept drift-tolerant case-base editing technique,” Artif. Intell., vol. 230, pp. 108–133, 2016.

[21] A. A. Qahtan, B. Alharbi, S. Wang, and X. Zhang, “A pca-based change detection framework for multidimensional data streams,” in Proc. 21th Int. Conf. on Knowledge Discovery and Data Mining. ACM, 2015, Conference Proceedings, pp. 935–944.

[22] F. Gu, G. Zhang, J. Lu, and C.-T. Lin, “Concept drift detection based on equal density estimation,” in Proc. 2016 Int. Joint Conf. Neural Networks. IEEE, 2016, Conference Proceedings, pp. 24–30.

[23] L. Bu, D. Zhao, and C. Alippi, “An incremental change detection test based on density difference estimation,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. PP, no. 99, pp. 1–13, 2017.

[24] A. Liu, Y. Song, G. Zhang, and J. Lu, “Regional concept drift detection and density synchronized drift adaptation,” in Proc. 26th Int. Joint Conf. Artificial Intelligence. Accept, 2017, Conference Proceedings.

[25] W. Heng and Z. Abraham, “Concept drift detection for streaming data,” in Proc. 2015 Int. Joint Conf. Neural Networks, 2015, Conference Proceedings, pp. 1–9.

[26] Y. Zhang, G. Chu, P. Li, X. Hu, and X. Wu, “Three-layer concept drifting detection in text data streams,” Neurocomputing, vol. 260, pp. 393–403, 2017.

[27] C. Alippi, G. Boracchi, and M. Roveri, “Hierarchical changedetection tests,” IEEE Trans. Neural Networks Learn. Syst., vol. 28, no. 2, pp. 246–258, 2017.

[28] S. Yu and Z. Abraham, “Concept drift detection with hierarchical hypothesis testing,” in Proc. 2017 SIAM Int. Conf. Data Mining. SIAM, 2017, Conference Proceedings, pp. 768–776.

[29] D. Liu, Y. Wu, and H. Jiang, “Fp-elm: An online sequential learning algorithm for dealing with concept drift,” Neurocomputing, vol. 207, pp. 322–334, 2016.

[30] S. G. Soares and R. Araujo, “An adaptive ensemble of on-line ´ extreme learning machines with variable forgetting factor for dynamic system prediction,” Neurocomputing, vol. 171, pp. 693– 707, 2016.

[31] H. M. Gomes, A. Bifet, J. Read, J. P. Barddal, F. Enembreck, B. Pfharinger, G. Holmes, and T. Abdessalem, “Adaptive random forests for evolving data stream classification,” Machine Learning, 2017.

[32] J. Z. Kolter and M. A. Maloof, “Dynamic weighted majority: An ensemble method for drifting concepts,” Journal of Machine Learning Research, 2007

[33] R. Elwell and R. Polikar, “Incremental learning of concept drift in nonstationary environments,” IEEE Trans. Neural Networks, vol. 22, no. 10, pp. 1517–31, 2011

[34] D. Brzezinski and J. Stefanowski, “Reacting to different types of concept drift: The accuracy updated ensemble algorithm,” IEEE Trans. Neural Networks Learn. Syst., vol. 25, no. 1, pp. 81–94, 2014.

[35] P. Zhang, X. Zhu, and Y. Shi, “Categorizing and mining concept drifting data streams,” in Proc. 14th ACM SIGKDD Int. Conf. Knowledge Discovery and Data Mining. Las Vegas, Nevada, USA: ACM, 2008, Conference Paper, pp. 812–820.

[36] P. Domingos and G. Hulten, “Mining high-speed data streams,” in Proc. 6th ACM SIGKDD Int. Conf. Knowledge Discovery and Data Mining. ACM, 2000, Conference Proceedings, pp. 71–80.

[37] G. Hulten, L. Spencer, and P. Domingos, “Mining time-changing data streams,” in Proc. 7th ACM SIGKDD Int. Conf. Knowledge Discovery and Data Mining. San Francisco, California: ACM, 2001, Conference Paper, pp. 97–106.

[38] J. Gama, R. Rocha, and P. Medas, “Accurate decision trees for mining high-speed data streams,” in Proc. 9th ACM SIGKDD Int. Conf. Knowledge Discovery and Data Mining. ACM, 2003, Conference Proceedings, pp. 523–528.

[39] H. Yang and S. Fong, “Incrementally optimized decision tree for noisy big data,” in Proc. 1st Int. Workshop Big Data, Streams and Heterogeneous Source Mining Algorithms, Systems, Programming Models and Applications. Beijing, China: ACM, 2012, Conference Paper, pp. 36–44.

[40] ——, “Countering the concept-drift problems in big data by an incrementally optimized stream mining model,” Journal of Systems and Software, vol. 102, pp. 158–166, 2015.

[41] L. Rutkowski, M. Jaworski, L. Pietruczuk, and P. Duda, “Decision trees for mining data streams based on the gaussian approximation,” IEEE Trans. Knowl. Data Eng., vol. 26, no. 1, pp. 108–119, 2014.

[42] L. Rutkowski, L. Pietruczuk, P. Duda, and M. Jaworski, “Decision trees for mining data streams based on the mcdiarmid’s bound,” IEEE Trans. Knowl. Data Eng., vol. 25, no. 6, pp. 1272–1279, 2013.

[43] A. Bifet, G. Holmes, B. Pfahringer, and E. Frank, “Fast perceptron decision tree learning from evolving data streams,” in Proc. 14th Pacific-Asia Conf. Knowledge Discovery and Data Mining, M. J. Zaki, J. X. Yu, B. Ravindran, and V. Pudi, Eds. Berlin, Heidelberg: Springer Berlin Heidelberg, 2010, Book Section, pp. 299–310.

[44] J. Cohen, “A coefficient of agreement for nominal scales,” Educational and Psychological Measurement, vol. 20, no. 1, pp. 37–46, 1960.

[45] I. Zliobait ˇ e, A. Bifet, J. Read, B. Pfahringer, and G. Holmes, ˙ “Evaluation methods and decision theory for classification of streaming data with temporal dependence,” Machine Learning, vol. 98, no. 3, pp. 455–482, 2015.

[46] D. Brzezinski and J. Stefanowski, “Prequential auc for classifier evaluation and drift detection in evolving data streams,” in Proc. 3rd Int. Workshop New Frontiers in Mining Complex Patterns, A. Appice, M. Ceci, C. Loglisci, G. Manco, E. Masciari, and Z. W. Ras, Eds. Cham: Springer International Publishing, 2014, Book Section, pp. 87–101.

[47] S. Yu, X. Wang, and J. C. Principe, “Request-and-reverify: Hierarchical hypothesis testing for concept drift detection with expensive labels,” arXiv preprint arXiv:1806.10131, 2018.