2018icpc南京现场赛-G Pyramid(打标找规律+逆元)

题意：

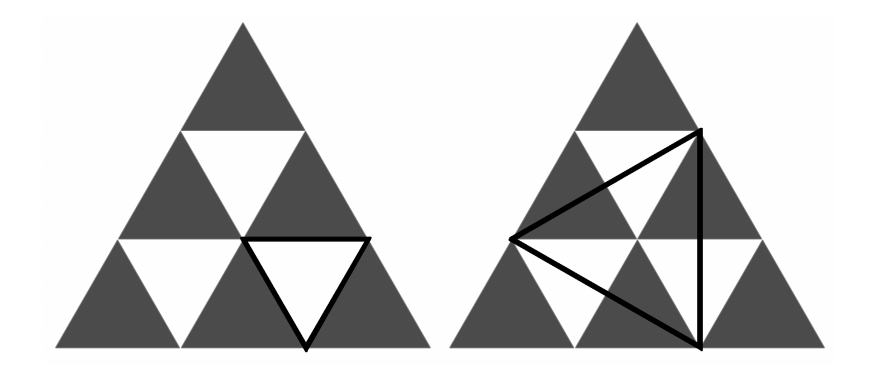
求n行三角形中等边三角形个数，图二的三角形也算。

n<=1e9

思路：

打表找下规律，打表方法：把所有点扔坐标系里n^3爆搜即可

打出来为 1，5，15，35，70，126，210..

没感觉，作差 4, 10, 20, 35, 56, 84

还是没感觉，作差 6, 10, 15, 21, 28

发现此时的差递增1？也就是再作差4, 5, 6, 7是等差数列

也就是再作差1, 1, 1为常数

相当于函数$A_n$求四次导为常数！(如果他是个连续函数的话)

于是我们设$\displaystyle A_n = a*n^4+b*n^3+c*n^2+d*n+e$ (别忘记常数)

解出a, b, c, d, e，

然后逆元+O(1)代公式就完事了

打表代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<string>
//#include<stack>
#include<queue>
#include<deque>
#include<set>
#include<vector>
#include<map>
#include<functional>
    
#define fst first
#define sc second
#define pb push_back
#define mem(a,b) memset(a,b,sizeof(a))
#define lson l,mid,root<<1
#define rson mid+1,r,root<<1|1
#define lc root<<1
#define rc root<<1|1
#define lowbit(x) ((x)&(-x)) 
#define mp make_pair

using namespace std;

typedef double db;
typedef long double ldb;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> PI;
typedef pair<ll,ll> PLL;

const db eps = 1e-6;
const int mod = 1e9+7;
const int maxn = 2e6+100;
const int maxm = 2e6+100;
const int inf = 0x3f3f3f3f;
const db pi = acos(-1.0);

vector<pair<double,double> >v;
struct point{
    double x, y;
    point(){}
    point(double a, double b){x = a; y = b;}
};
double h = 0.5 *sqrt(3);
double len(pair<double,double>a, pair<double,double>b){
    return (a.fst-b.fst)*(a.fst-b.fst)+(a.sc-b.sc)*(a.sc-b.sc);
}
bool eq(double a, double b){
    if(fabs(a-b)<1e-6)return true;
    return false;
}
int main(){
    v.pb(mp(0,0));
    for(int i = 1; i <= 2000; i++){
        if(i&1){
            for(int j = 0; j < i/2+1; j++){
                v.pb(mp(j*1.0+0.5,-i*h));
                v.pb(mp(-j*1.0-0.5,-i*h));
            }
        }
        else{
            v.pb(mp(0,-i*h));
            for(int j = 1; j <= i/2; j++){
                v.pb(mp(j*1.0,-i*h));
                v.pb(mp(-j*1.0,-i*h));
            }
        }
        int cnt = 0;
        for(int j = 0; j < (int)v.size(); j++){
            for(int k = j+1; k < (int)v.size(); k++){
                for(int g = k+1; g < (int)v.size(); g++){
                    if(eq(len(v[j],v[k]),len(v[k],v[g]))&&eq(len(v[j],v[k]),len(v[j],v[g])))cnt++;
                }
            }
        }
        printf("%d\n",cnt);
    }

    return 0;
}
/*
3 5 0
4 1 2 3 5
2 2 5
2 1 2


5 10 2
2 3 10
5 1 3 4 6 10
5 3 4 6 8 9
3 1 9 10
5 1 3 6 7 10

 */