信号与系统05 拉普拉斯变换

1. 拉普拉斯变换

• 1. 拉普拉斯变换
  • 1.1. 定义
    • 1.1.1. 计算公式
    • 1.1.2. 收敛域的计算
    • 1.1.3. 拉氏变换与傅氏变换的关系
  • 1.2. 性质
    • 1.2.1. 线性
    • 1.2.2. 时移
    • 1.2.3. 复频移
    • 1.2.4. 尺度变换
    • 1.2.5. 时域微分特性
    • 1.2.6. \(s\) 域微分特性
    • 1.2.7. 时域积分特性
    • 1.2.8. \(s\) 域积分特性
    • 1.2.9. 时域卷积定理
    • 1.2.10. 初值定理
    • 1.2.11. 终值定理
  • 1.3. 常见的拉氏变换对
    • 1.3.1. 直流或正幂项
    • 1.3.2. 单根极点
    • 1.3.3. 共轭复根极点
    • 1.3.4. 重根极点
    • 1.3.5. 周期极点

---

1.1. 定义

1.1.1. 计算公式

\[\begin{aligned} F(s) &= \int_{-\infty}^{\infty} f(t) e^{-st} dt\\ f(t) &= \frac{1}{2\pi j} \int_{\sigma - j\infty}^{\sigma + j\infty} F(s) e^{st} ds \end{aligned} \]

其中，\(s\) 是一个复数，可以写为 \(s = \sigma + jw\)；
\(f(t)e^{-st} = f(t)e^{-\sigma t} \cdot e^{-jwt}\)，有点类似对 \(f(t)e^{-\sigma t}\) 进行傅氏变换。

1.1.2. 收敛域的计算

因为增加了一个收敛因子 \(e^{-\sigma t}\) ，只要找到合适的 \(\sigma\) 就可以使得 \(f(t)e^{-\sigma t}\) 绝对收敛，即

\[\displaystyle\lim_{t\to \pm \infty} f(t) e^{-\sigma t} = 0 \]

满足此式的 \(s\) 值的范围内称为拉氏变换的收敛域。

主要分为 4 种情况：右边信号，左边信号，双边信号，时限信号；

• 右边信号

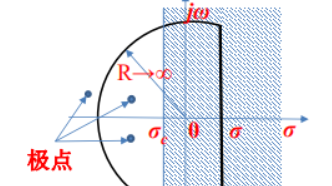
  右边信号的收敛域往往包含复平面的右半面，（非严谨）证明如下：

  对于右边信号，当 \(t < t_0\) 有 \(f(t) \equiv 0\)，始终满足

  \[\forall \sigma \in R, \lim_{t \to -\infty} f(t) e^{-\sigma t} = 0 \]

  因此只需要考虑趋于正无穷的情况；

  当 \(t \ge t_0\) 时，假设 \(\sigma_0\) 使得 \(f(t)e^{-\sigma t}\) 绝对收敛。令 \(\sigma_1 > \sigma_0\)，由于 \(e^{-\sigma_1 t}\) 的收敛速度\((t\to +\infty)\)比 \(e^{-\sigma_0 t}\) 更快，所以 \(\sigma_1 > \sigma_0\) 也能使得 \(f(t)e^{-\sigma t}\) 绝对收敛，即对于右边信号，如果在一个点上收敛，则这个点的右边所有点均收敛。

• 左边信号

  左边信号的收敛域往往包含复平面的左半边，证明过程也是类似的。

  当 \(t \le t_0\) 时，假设 \(\sigma_0\) 使得 \(f(t)e^{-\sigma t}\) 绝对收敛。令 \(\sigma_2 < \sigma_0\)，由于 \(e^{-\sigma_2 t}\) 的收敛速度\((t\to -\infty)\)比 \(e^{-\sigma_0 t}\) 更快，所以 \(\sigma_2 < \sigma_0\) 也能使得 \(f(t)e^{-\sigma t}\) 绝对收敛，即对于左边信号，如果在一个点上收敛，则这个点的左边所有点均收敛。

• 双边信号

  双边信号的收敛域为带状或不存在。

  双边信号可以分解为左边信号和右边信号，当且仅当左边信号和右边信号的收敛域存在交集时，双边信号才存在拉氏变换。

• 时限信号

  实现信号的收敛域为整个复平面。对于时限信号，有

  \[\lim_{t \to \pm \infty} f(t) = 0 \]

  所以有

  \[\forall \sigma \in R, \lim_{t \to \pm \infty} f(t) e^{-\sigma t}= 0 \]

  典型的时限信号有：\(\delta(t)\)，\(G_{\tau}(t)\) 等

1.1.3. 拉氏变换与傅氏变换的关系

根据收敛域分为 3 种情况：

• 收敛域包含虚轴

  拉氏变换与傅氏变换满足：\(F(jw) = F(s)|_{s=jw}\)

• 收敛域以虚轴为界

  拉氏变换与傅氏变换无明显关系 \(F(jw) \not = F(s)|_{s=jw}\)，例如 \(u(t)\) 的拉氏变换为 \(\frac{1}{s}\)，其傅氏变换为 \(\frac{1}{jw} + \pi \delta(w)\)。

• 收敛域不包含虚轴

  只存在的拉氏变换，不存在傅氏变换。

1.2. 性质

1.2.1. 线性

\[\mathscr{L}[af_1(t) + bf_2(t)] = aF_1(s) + bF_2(s) \]

1.2.2. 时移

\[\mathscr{L}[f(t)u(t)] = F(s),\\\mathscr{L}[f(t-t_0)u(t-t_0)] = F(s)e^{-st_0} \]

1.2.3. 复频移

\[\mathscr{L}[f(t)e^{s_0t}] = F(s-s_0) \]

1.2.4. 尺度变换

\[\mathscr{L}[f(at)] = \frac{1}{a}F(\frac{s}{a}),\ a > 0 \]

1.2.5. 时域微分特性

\[\mathscr{L}[\displaystyle\frac{d f(t)}{dt}] = sF(s) - f(0^-),\\ \mathscr{L}[\displaystyle\frac{d^2 f(t)}{dt^2}] = s^2F(s) - sf(0^-) - sf'(0^-)\\ \]

1.2.6. \(s\) 域微分特性

\[\mathscr{L}[(-t)f(t)] = \frac{dF(s)}{ds} \]

1.2.7. 时域积分特性

\[\mathscr{L}\left[\int_{-\infty}^{t} f(\tau) d\tau \right] = \frac{F(s)}{s} + \frac{f^{-1}(0)}{s} \]

1.2.8. \(s\) 域积分特性

\[\mathscr{L}\left[\frac{f(t)}{t}\right] = \int_{s}^{+\infty} F(s_1) ds_1 \]

1.2.9. 时域卷积定理

\[\mathscr{L}[f(t)*g(t)] = F(s)G(s) \]

1.2.10. 初值定理

\[\displaystyle\lim_{s \to +\infty}s\cdot F(s) = f(0^+) \]

初值定理要求：

1. \(f(t)\) 连续可导；
2. 不包含任何阶次的冲激函数；
3. \(F(s)\) 是真有理分式

1.2.11. 终值定理

\[\displaystyle\lim_{s \to 0} s \cdot F(s) = f(+\infty) \]

终值定理要求： \(x(t)\) 的终值存在，即 \(X(s)\) 的极点在左半 \(s\) 平面

1.3. 常见的拉氏变换对

1.3.1. 直流或正幂项

• 冲激信号

\[\mathscr{L}[\delta(t)] = 1,\ \sigma \in R \]

• 冲激偶信号
  \[\mathscr{L}[\delta'(t)]=s,\ \sigma \in R \]

1.3.2. 单根极点

• 阶跃信号

  \[\mathscr{L}[u(t)] = \frac{1}{s},\ \sigma > 0 \]

• 单边指数信号

  \[\mathscr{L}[e^{at}u(t)] = \frac{1}{s-a},\ \sigma>a,\\\mathscr{L}[e^{at}u(-t)] = -\frac{1}{s-a},\ \sigma<a \]

• 双边指数信号

\[\mathscr{L}[e^{-a\|t\|}] = \frac{2a}{a^2-s^2},\ \sigma\in(-a,a) \]

1.3.3. 共轭复根极点

• 正弦信号
  \[\displaystyle\mathscr{L}[\sin(w_0 t)u(t)] = \frac{w_0}{s^2 + w_0^2},\ \sigma > 0 \]

• 余弦信号
  \[\displaystyle\mathscr{L}[\cos(w_0 t)u(t)] = \frac{s}{s^2 + w_0^2},\ \sigma > 0 \]

• 正弦衰减信号
  \[\displaystyle\mathscr{L}[e^{at}\sin(w_0 t)u(t)] = \frac{w_0}{(s-a)^2 + w_0^2},\ \sigma > a \]

• 余弦衰减信号
  \[\displaystyle\mathscr{L}[e^{at}\cos(w_0 t)u(t)] = \frac{s-a}{(s-a)^2 + w_0^2},\ \sigma > a \]

1.3.4. 重根极点

• 斜变信号
  \[\displaystyle\mathscr{L}[tu(t)] = \frac{1}{s^2},\ \sigma > 0 \]

• 高阶斜变信号
  \[\displaystyle\mathscr{L}\left[\frac{t^n}{n!} u(t)\right] = \frac{1}{s^{n+1}},\ \sigma > 0 \]

• 斜变衰减信号
  \[\displaystyle\mathscr{L}\left[\frac{t^n}{n!} e^{at} u(t)\right] = \frac{1}{(s-a)^{n+1}},\ \sigma > a \]

1.3.5. 周期极点

• 周期冲激信号
  \[\displaystyle\mathscr{L}\left[\sum_{n=0}^{+\infty}\delta(t - nT)\right] = \frac{1}{1 - e^{-sT}},\ \sigma \not = 0 \]

---

对于有理分式，求解拉氏逆变换最常用的方式是部分分式分解法。一个有理分式可以表示为

\[H(s) = \frac{B(s)}{A(s)} = \frac{\displaystyle\sum_{n=0}^{N} b_n s^n}{\displaystyle\sum_{m=0}^{M} a_m s^m}\]

部分分式分解建立在极点分解的基础。极点即是分母 \(A(s)\) 的根，它有三中类型，即单根极点、共轭复根极点和重根极点，根据三种极点类型，该分式可以分解为

\[H(s) = \sum_{i} \frac{A_i}{s-p_i} + \sum_{j} \frac{B_j s + C_j}{(s+\alpha_j)^2 + \beta_j^2} + \sum_{m} \sum_{r=1}^{k} \frac{D_r}{(s-p_m)^r} \]

其中，

• \(p_i\) 是单根极点，对应的是阶跃信号、指数信号的变换式；
• \(\alpha_j \pm j \beta_j\) 是共轭复根极点，对应的是正弦信号和正弦衰减信号的变换式；
• \(p_m\) 是 \(k\) 阶重根极点，对应的是斜变信号以及和斜变信号相乘的信号的变换式；
• 若有理分式为假分式，则可能存在直流项或正幂次项，对应的是冲激信号或高阶冲激信号。

---

点击查看

常见的拉普拉斯变换对 - 对查表

拉普拉斯变换的性质 - 对查表