激活函数:Sigmod&tanh&Softplus&Relu详解
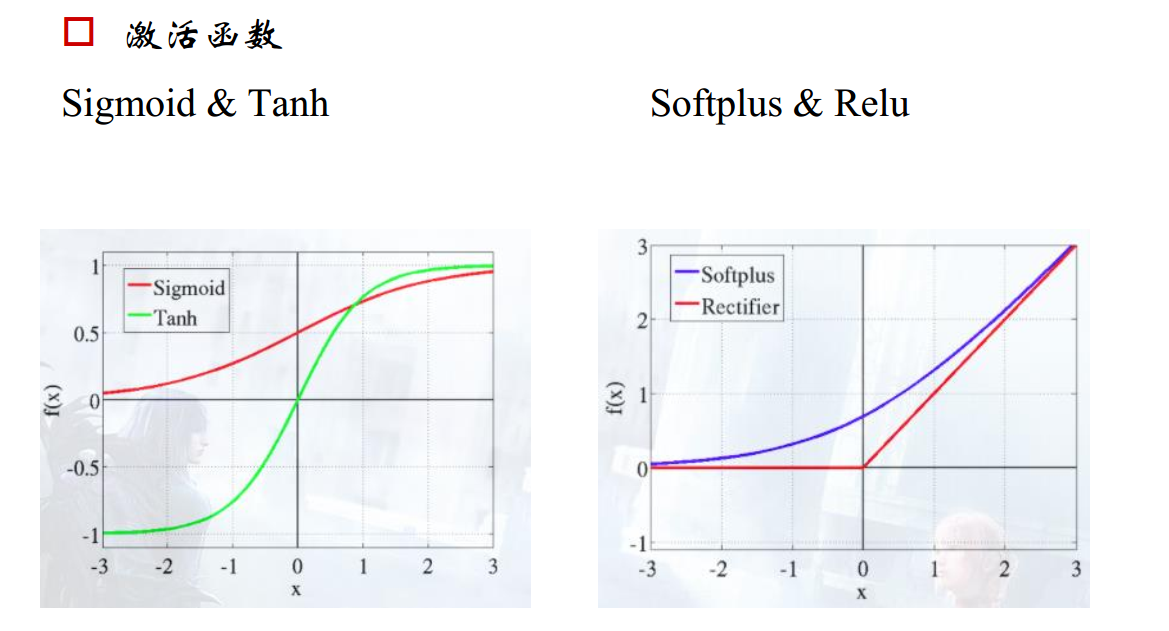
什么是激活函数?
激活函数(Activation functions)对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说具有十分重要的作用。
它们将非线性特性引入到我们的网络中。其主要目的是将A-NN模型中一个节点的输入信号转换成一个输出信号。该输出信号现在被用作堆叠中下一个层的输入。
如果我们不运用激活函数的话,则输出信号将仅仅是一个简单的线性函数。线性函数一个一级多项式。现如今,线性方程是很容易解决的,但是它们的复杂性有限,并且从数据中学习复杂函数映射的能力更小。
一个没有激活函数的神经网络将只不过是一个线性回归模型(Linear regression Model)罢了,它功率有限,并且大多数情况下执行得并不好。我们希望我们的神经网络不仅仅可以学习和计算线性函数,而且还要比这复杂得多。
同样是因为没有激活函数,我们的神经网络将无法学习和模拟其他复杂类型的数据,例如图像、视频、音频、语音等。这就是为什么我们要使用人工神经网络技术,诸如深度学习(Deep learning),来理解一些复杂的事情,一些相互之间具有很多隐藏层的非线性问题,而这也可以帮助我们了解复杂的数据。
那么为什么我们需要非线性函数?
非线性函数是那些一级以上的函数,而且当绘制非线性函数时它们具有曲率。现在我们需要一个可以学习和表示几乎任何东西的神经网络模型,以及可以将输入映射到输出的任意复杂函数。
神经网络被认为是通用函数近似器(Universal Function Approximators)。这意味着他们可以计算和学习任何函数。几乎我们可以想到的任何过程都可以表示为神经网络中的函数计算。
而这一切都归结于这一点,我们需要应用激活函数f(x),以便使网络更加强大,增加它的能力,使它可以学习复杂的事物,复杂的表单数据,以及表示输入输出之间非线性的复杂的任意函数映射。因此,使用非线性激活函数,我们便能够从输入输出之间生成非线性映射。
激活函数的另一个重要特征是:它应该是可以区分的。我们需要这样做,以便在网络中向后推进以计算相对于权重的误差(丢失)梯度时执行反向优化策略,然后相应地使用梯度下降或任何其他优化技术优化权重以减少误差。
激活函数
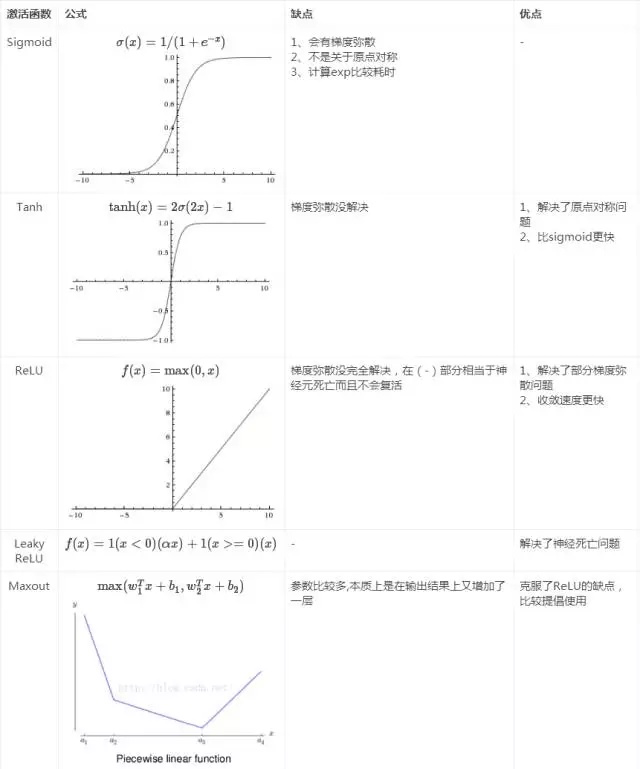
激活函数的发展经历了Sigmoid -> Tanh -> ReLU -> Leaky ReLU -> Maxout这样的过程,还有一个特殊的激活函数Softmax,因为它只会被用在网络中的最后一层,用来进行最后的分类和归一化。本文简单来梳理这些激活函数是如何一步一步演变而来的。
总结如下,先贴图:
Sigmoid
数学公式:
sigmoid非线性函数的数学公式是
函数图像如下图所示。它输入实数值并将其“挤压”到0到1范围内,适合输出为概率的情况,但是现在已经很少有人在构建神经网络的过程中使用sigmoid。
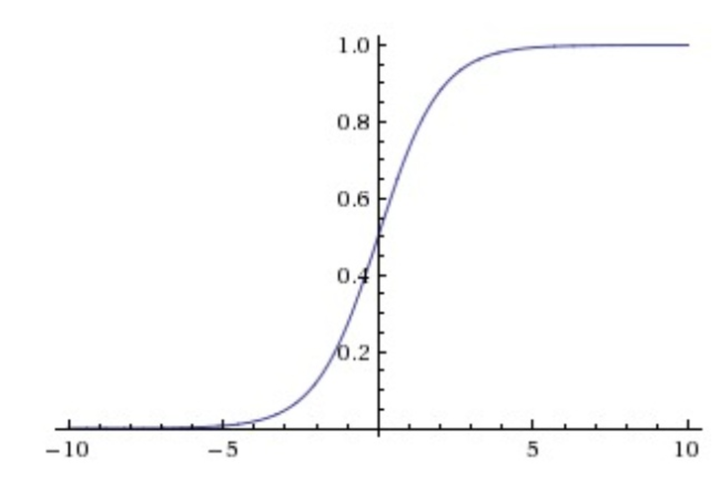 Sigmoid函数图像
Sigmoid函数图像
存在问题:
- Sigmoid函数饱和使梯度消失。当神经元的激活在接近0或1处时会饱和,在这些区域梯度几乎为0,这就会导致梯度消失,几乎就有没有信号通过神经传回上一层。
- Sigmoid函数的输出不是零中心的。因为如果输入神经元的数据总是正数,那么关于
的梯度在反向传播的过程中,将会要么全部是正数,要么全部是负数,这将会导致梯度下降权重更新时出现z字型的下降。
Tanh
数学公式:
Tanh非线性函数的数学公式是
Tanh非线性函数图像如下图所示,它将实数值压缩到[-1,1]之间。
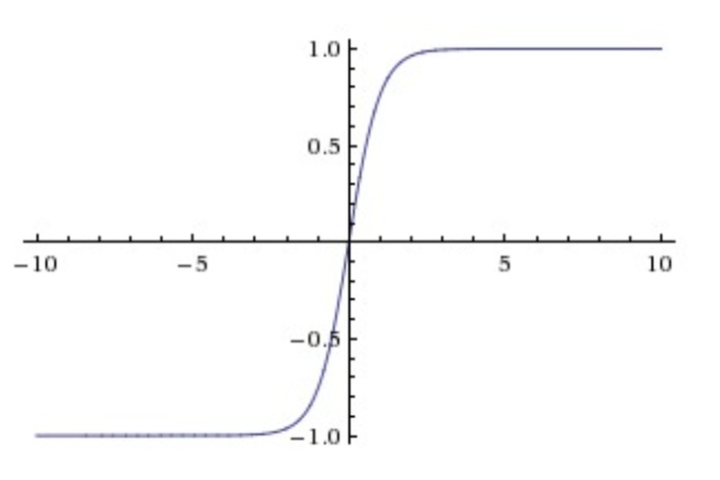 Tanh函数图像
Tanh函数图像
存在问题:
Tanh解决了Sigmoid的输出是不是零中心的问题,但仍然存在饱和问题。
为了防止饱和,现在主流的做法会在激活函数前多做一步batch normalization,尽可能保证每一层网络的输入具有均值较小的、零中心的分布。
ReLU
数学公式:
函数公式是
ReLU非线性函数图像如下图所示。相较于sigmoid和tanh函数,ReLU对于随机梯度下降的收敛有巨大的加速作用;sigmoid和tanh在求导时含有指数运算,而ReLU求导几乎不存在任何计算量。
对比sigmoid类函数主要变化是:
1)单侧抑制;
2)相对宽阔的兴奋边界;
3)稀疏激活性。
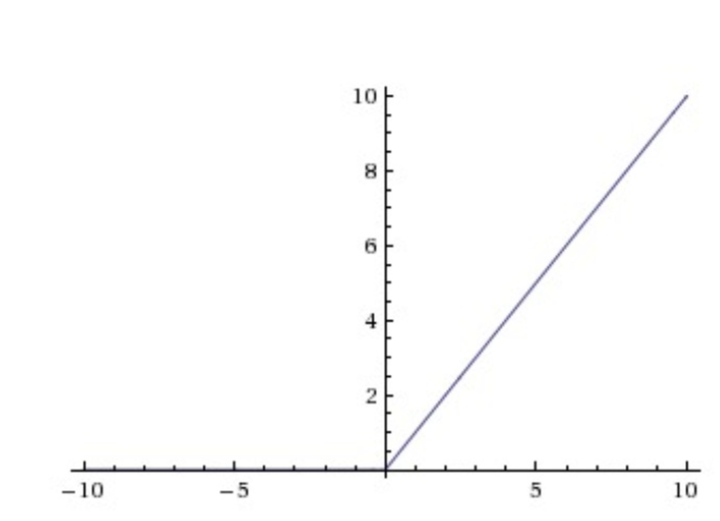 ReLU函数图像
ReLU函数图像
存在问题:
ReLU单元比较脆弱并且可能“死掉”,而且是不可逆的,因此导致了数据多样化的丢失。通过合理设置学习率,会降低神经元“死掉”的概率。
Leaky ReLU
数学公式:
函数公式是
其中 是很小的负数梯度值,比如0.01,Leaky ReLU非线性函数图像如下图所示。这样做目的是使负轴信息不会全部丢失,解决了ReLU神经元“死掉”的问题。更进一步的方法是PReLU,即把
当做每个神经元中的一个参数,是可以通过梯度下降求解的。
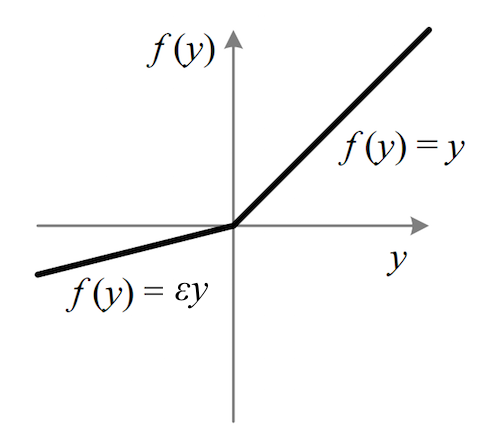 Leaky ReLU函数图像
Leaky ReLU函数图像
Maxout
数学公式:
Maxout是对ReLU和leaky ReLU的一般化归纳,函数公式是
Maxout非线性函数图像如下图所示。Maxout具有ReLU的优点,如计算简单,不会 saturation,同时又没有ReLU的一些缺点,如容易go die。
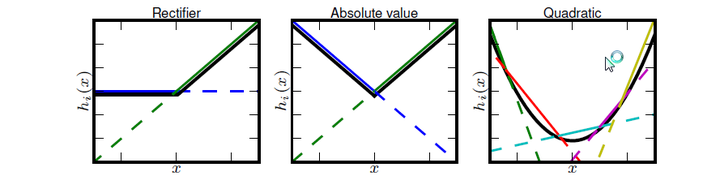 Maxout函数图像
Maxout函数图像
存在问题:
每个神经元的参数double,这就导致整体参数的数量激增。
Softmax
数学公式:
Softmax用于多分类神经网络输出,目的是让大的更大。函数公式是
示意图如下。
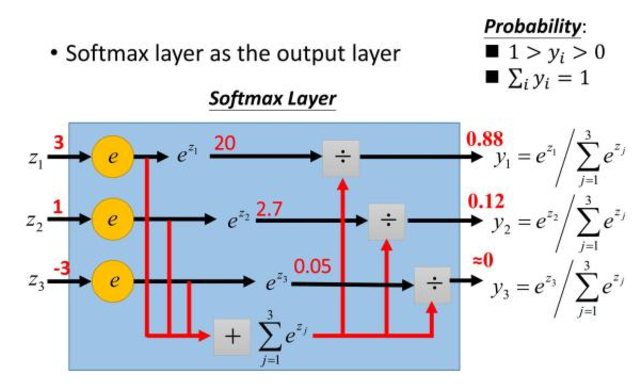 Softmax示意图
Softmax示意图
Softmax是Sigmoid的扩展,当类别数k=2时,Softmax回归退化为Logistic回归。
激活函数中的 Triangular basis 函数怎样定义?有何意义?
定义
Triangular basis 函数的图像如下:
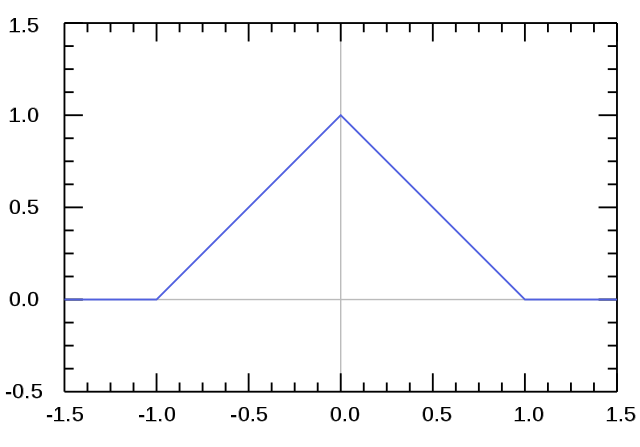
看成分段函数的话,定义是显然的:
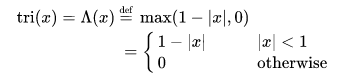
意义
回过头去看下Triangular basis函数的图像,这个形状能让你联想到什么?
也许你会想到ReLU(Rectified Linear Unit,修正线性单元)激活函数:
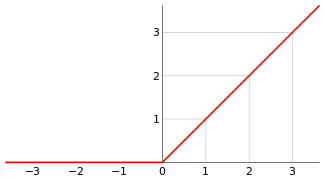 许可:公有领域
许可:公有领域
没错,实际上Triangular basis可以看成两个ReLU拼起来(卷积):
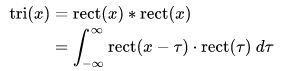
不过现在让我们再想想,Triangular basis的形状还能联想到什么?
也许你想到了,高斯(Gaussian)函数(钟形曲线):
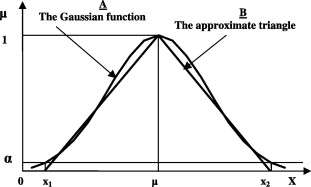 图片来源:doi.org/10.1016/j.eij.2013.04.001
图片来源:doi.org/10.1016/j.eij.2013.04.001
是的,Triangular basis函数可以看成是对高斯函数的逼近。当然,相比高斯函数,Triangular basis的计算量要小很多。
我们之前刚刚说到Triangular basis函数很像ReLU。实际上,我们可以仿照ReLU函数的定义 ,将Triangular basis函数定义为
。
将Triangular basis函数定义改写之后,我们能够很清楚地看到,Triangular basis函数的计算量,基本上和ReLU差不多。
而ReLU激活函数的一大优势就是在算力上更经济(使用的是比较简单的数学运算),可以加快深度神经网络的训练速度。Triangular basis激活函数在这一点上和ReLU很像,算力负担很轻。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号