Softmax函数与交叉熵
在Logistic regression二分类问题中,我们可以使用sigmoid函数将输入Wx+b映射到(0,1)区间中,从而得到属于某个类别的概率。将这个问题进行泛化,推广到多分类问题中,我们可以使用softmax函数,对输出的值归一化为概率值
这里假设在进入softmax函数之前,已经有模型输出C值,其中C是要预测的类别数,模型可以是全连接网络的输出aa,其输出个数为C,即输出为:
所以对每个样本,它属于类别i的概率为:
通过上式可以保证 ,即属于各个类别的概率和为1
对softmax函数进行求导,即求: ,第i项的输出对第j项输入的偏导。代入
softmax函数表达式,可以得到:
求导规则:对于 ,导数为:
所以在我们这个例子中,
上面两个式子只是代表直接进行替换,而非真的等式。 ,(即g(x)=
对
进行求导),要分情况讨论:
- 如果i=j,则求导结果为
- 如果i≠j,则求导结果为0
再来看 对
求导,结果为
所以,当i=j时:(其中,为了方便,令 )
当i≠j时:
标红下,这俩公式很重要:
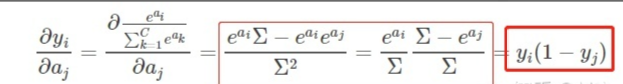
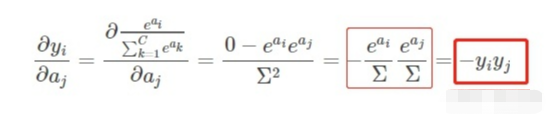
大多数人都以为是才智成就了科学家,他们错了,是品格。---爱因斯坦



 浙公网安备 33010602011771号
浙公网安备 33010602011771号