数据结构|-完全二叉树的顺序存储结构的实现

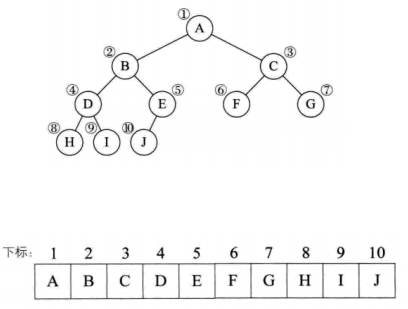
对于一个完全二叉树，假设它有n个结点，对结点进行从1开始编号，对任一结点i满足下面

• 它的双亲是结点 i/2 (除了i=1的情况)
• 左孩子是 2i 右孩子是 2i+1
• 如果2i>n 说明无左孩子 2i+1>n 说明无右孩子

一般的树来说是一对多的关系，使用顺序结构存储起来比较困难，但是二叉树是一种特殊的树，每个结点最多有两个子节点，并且子节点有左右之分，并且兄弟，父亲，孩子可以很方便的通过编号得到，所以我们使用顺序存储结构使用二叉树的存储。

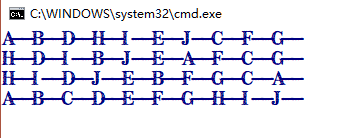
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace TestFun3
{
    class Program
    {
        static void Main(string[] args)
        {
            BiTree<string> tree = new BiTree<string>(16);

            tree.Add("A"); tree.Add("B"); tree.Add("C"); tree.Add("D");
            tree.Add("E"); tree.Add("F"); tree.Add("G"); tree.Add("H"); tree.Add("I");
            tree.Add("J");

            tree.PreTravelsal(); Console.WriteLine();
            tree.InorderTraversal(); Console.WriteLine();
            tree.PostTraversal(); Console.WriteLine();
            tree.LevelTraversal(); Console.WriteLine();


            Console.ReadKey();

        }
    }

    /// <summary>
    /// 二叉树的顺序存储结构
    /// </summary>
    /// <typeparam name="T"></typeparam>
    class BiTree<T>
    {
        private T[] data;//二叉树的数据
        private int count;//二叉树结点个数

        /// <summary>
        /// 创建二叉树
        /// </summary>
        /// <param name="capcity">二叉树容量</param>
        public BiTree(int capcity)
        {
            //指定二叉树的容量（顺序存储结构都必须事先指定存储容量）
            data = new T[capcity];
        }

        /// <summary>
        /// 添加结点元素
        /// </summary>
        /// <param name="item">元素</param>
        /// <returns>返回false表示二叉树容量已满，添加失败</returns>
        public bool Add(T item)
        {
            //首先做安全校验
            if (count >= data.Length) return false;
            data[count] = item;
            count++;
            return true;
        }

        //前序遍历
        public void PreTravelsal() { PreTravelsal(0); }
        public void PreTravelsal(int index)
        {
            if (index >= count) return;
            //二叉树中的结点编号是index+1
            int number = index + 1;
            Console.Write(data[index] + "--");
            //找到当前结点的左子树
            PreTravelsal(number * 2 - 1);
            //找到当前结点的右子树
            PreTravelsal(number * 2 + 1 - 1);
        }

        //中序遍历
        public void InorderTraversal() { InorderTraversal(0); }
        public void InorderTraversal(int index)
        {
            if (index >= count) return;
            int number = index + 1;
            InorderTraversal(number * 2 - 1);
            Console.Write(data[index] + "--");
            InorderTraversal(number * 2 + 1 - 1);

        }

        //后序遍历
        public void PostTraversal() { PostTraversal(0); }
        public void PostTraversal(int index)
        {
            if (index >= count) return;
            int number = index + 1;
            PostTraversal(number * 2 - 1);
            PostTraversal(number * 2 + 1 - 1);
            Console.Write(data[index] + "--");
        }

        //层序遍历
        public void LevelTraversal()
        {
            for (int i = 0; i < count; i++)
            {
                Console.Write(data[i]+"--");
            }
            Console.WriteLine();
        }
    }
}