OO 第一单元总结
OO 第一单元总结
一、作业架构设计与分析
1、第一次作业
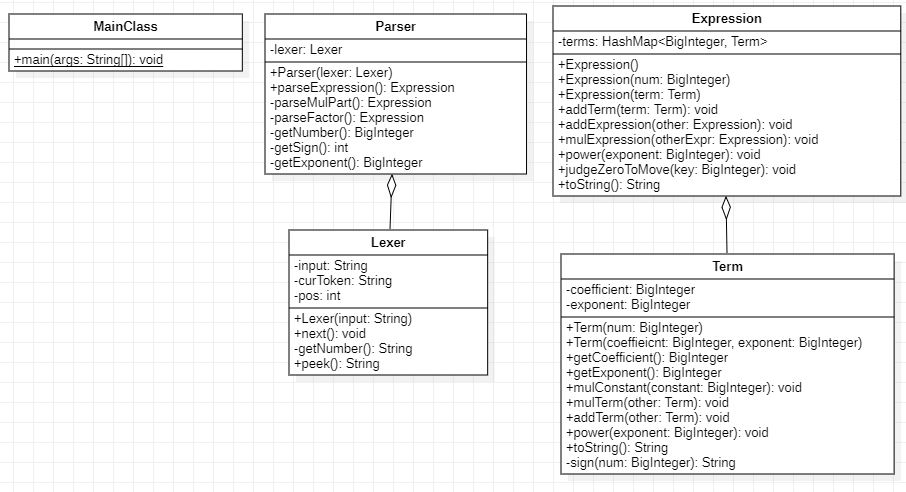
UML类图
类的设计
- Term 类用来存储单项式(a * x ** b)。
- coefficient 为系数。
- exponent 为指数。
- Expression 类用来存储表达式。
- terms 为一个 HashMap,用来存储单项式,该 HaspMap 以单项式的指数为 Key,单项式本身为 Value。
- Lexer 类用于做词法分析。
- Parser 类用于解析表达式。
表达式解析
我采用递归下降的方法解析表达式。从结构上看,整个表达式被加减法分成了若干个项,每个项又被乘号分成若干个因子,因此,可以以递归的方式依次解析表达式、项、因子。
在解析表达式的时候,我本想分别定义 Expression、Term、Factor 类,采用递归嵌套的方式来存储表达式,但是想不到一个比较好的合并同类项的方案,因此我转化了思路,采用线性方式来存储表达式,而在解析项和因子的时候,返回的都是一个表达式,这样就可以直接跟原有的表达式进行合并,不必采用递归嵌套的存储方式。这样做也使得 Parser 类中只进行表达式层面的运算,而表达式层面的运算在 Expression 类中进一步的落实到底层的类。
合并同类项
当需要将一个单项式加入到表达式中时,只需判断该单项式的指数是否有在 HashMap 的 KeySet 中,即可方便地进行同类项的合并。
2、第二次作业
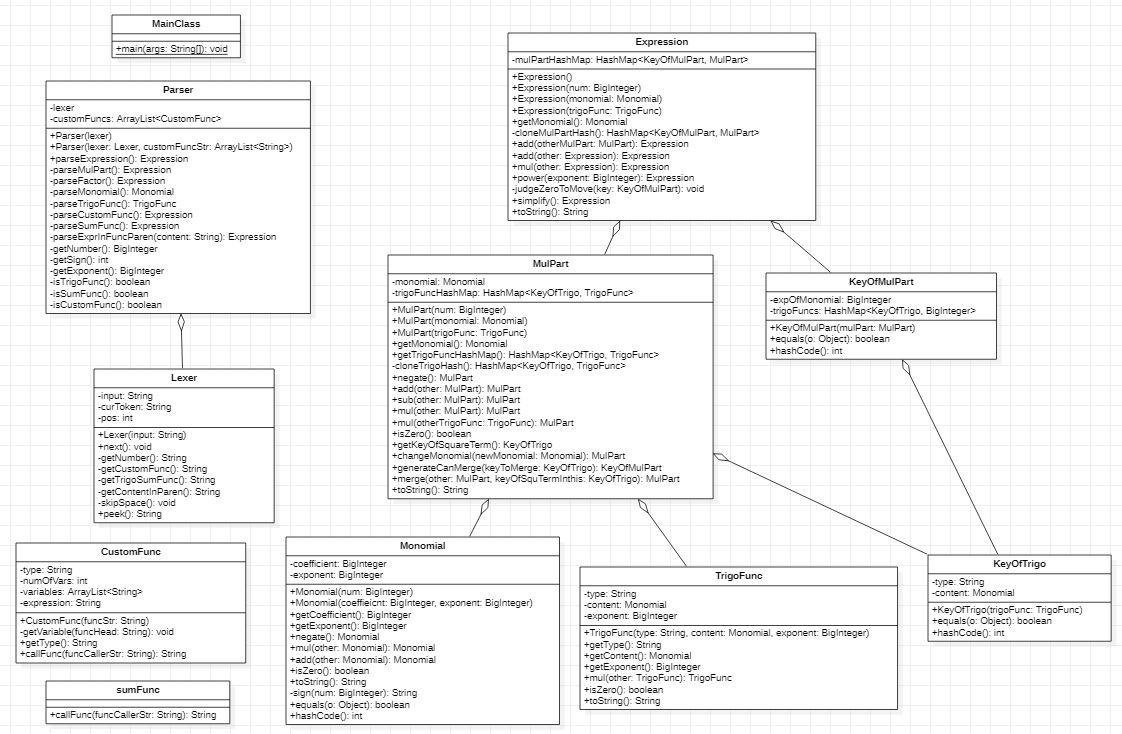
UML 类图
类的设计
-
将第一次作业中的 Term 重命名为 Monomial 用来存储单项式。
-
TrigoFunc 类用来存储三角函数。
- type 为类型(sin 或 cos)。
- content 为括号内的内容。
- exponent 为三角函数的指数。
-
KeyOfTrigo 为三角函数去掉指数后的部分,用来判断两个三角函数可否通过乘法进行合并。
-
MulPart 表示一个单项式乘以若干个三角函数。
- monomial 为单项式。
- trigoFuncHashMap 是用来存储三角函数的 HashMap,以 KeyOfTrigo 为 Key、TrigoFunc 为 Value。
-
KeyOfMulPart 是 MulPart 去掉常数系数以后的部分。
-
Expression 类用来存储表达式。
- mulPartHashMap 是用来存储 MulPart 的HashMap,以 KeyOfMulPart 为 Key、MulPart 为 Value。
-
SumFunc 表示求和函数。
-
CuntomFunc 表示自定义函数。
- type 为类型(f、g、h)。
- numOfVars 为自变量个数。
- variables 为自变量。
- expression 为函数表达式。
-
Lexer 类为词法分析器。
-
Parser 类用于解析表达式。
表达式解析
整体思路与第一次作业相同,对求和函数以及自定义函数的解析采用字符串替换的方案。
合并同类项
(1)三角函数乘法合并
两个三角函数能够通过乘法合并的条件为除指数以外的部分均相同,因此建立上文所述的 HashMap 来存储三角函数,当一个 MulPart 乘以一个三角函数时,只需判断该三角函数对应的 Key 是否在 HashMap 中即可方便的进行合并。
(2)MulPart 加法合并
两个 MulPart 能够通过加法合并的条件是系数不同。同理,可建立对应的 HashMap。
表达式化简
我在作业中只做了三角函数平方和的化简,方案如下:
对于 Expression 类,遍历 HashMap 的 Values,若遇到某一个 MulPart 含有 sin 或 cos 的平方,则将其替换为与之对应的可以通过平方和合并的三角函数(sin 替换成 cos,cos 替换成 sin),得到一个配对的 MulPart,接着判断这个 MulPart 的 Key 是否有在 HashMap 中,如果有,则可将两个 MulPart 进行合并。
下面举个例子:对 2*sin(x**2)**3 + sin(x**2)*cos(x**2)**2,我们对其进行遍历。第一项 +2*sin(x**2)**3 不含有平方项,跳过。第二项 +sin(x**2)*cos(x**2)**2 含有平方项,因此我们将 cos(x**2)**2 替换为 sin(x**2)**2 ,得到 +sin(x**2)*sin(x**2)**2,即 +sin(x**2)**3。此时我们发现 +sin(x**2)**3 的 Key 在原表达式中存在,对应 +2*sin(x**2)**3,因此我们将 +2*sin(x**2)**3 与 +sin(x**2)*cos(x**2)**2 进行合并,得到 sin(x**2)**3 + sin(x**2)。
3、第三次作业
UML 类图
类的设计
整体设计与第二次作业相同,修改了 TrigoFunc 的 content 属性为 Expression 类型。
表达式解析与化简
整体方案与第二次作业相同。由于意识到了字符串替换可能带来的问题,我修改了解析自定义函数的方法,不再采用字符串替换,而是对函数进行建模,将函数调用的实参逐个代入函数表达式。
4、优缺点分析
表达式解析
- 优点:不采用递归嵌套而采用线性的存储方式便于对表达式进行解析和运算。
- 缺点:难以建立一个统一的父类来管理所有因子,抽象程度不够高。
表达式化简
-
优点:能够快速查找能够进行平方和合并的项,效率较高。
-
缺点:仅进行一次线性扫描,无法合并彻底,可能出现下面这种情况
对于 sin(x)**2 + cos(x)**2*sin(x)**2 + cos(x)**4,cos(x)**2*sin(x)**2 与 cos(x)**4 合并成 cos(x)**2 后本应可以跟 sin(x)**2 继续合并,但由于我们没有对合并得到的 cos(x)**2 进行扫描,因此无法使之与 sin(x)**2 进一步合并。
二、代码度量分析
第一次作业
| class | OCavg | OCmax | WMC |
|---|---|---|---|
| Expression | 2.0 | 4.0 | 22.0 |
| Lexer | 3.0 | 8.0 | 12.0 |
| MainClass | 1.0 | 1.0 | 1.0 |
| Parser | 2.2857142857142856 | 4.0 | 16.0 |
| Term | 1.6 | 5.0 | 16.0 |
| Total | 67.0 | ||
| Average | 2.0303030303030303 | 4.4 | 13.4 |
第二次作业
| class | OCavg | OCmax | WMC |
|---|---|---|---|
| expression.CustomFunc | 2.5 | 6.0 | 10.0 |
| expression.Expression | 2.4615384615384617 | 9.0 | 32.0 |
| expression.key.KeyOfMulPart | 2.0 | 3.0 | 6.0 |
| expression.key.KeyOfTrigo | 1.6666666666666667 | 3.0 | 5.0 |
| expression.Monomial | 1.6666666666666667 | 5.0 | 20.0 |
| expression.MulPart | 1.8421052631578947 | 6.0 | 35.0 |
| expression.SumFunc | 4.0 | 4.0 | 4.0 |
| expression.TrigoFunc | 1.5714285714285714 | 4.0 | 11.0 |
| Lexer | 2.875 | 9.0 | 23.0 |
| MainClass | 2.0 | 2.0 | 2.0 |
| Parser | 1.9375 | 7.0 | 31.0 |
| Total | 179.0 | ||
| Average | 2.057471264367816 | 5.2727272727272725 | 16.272727272727273 |
第三次作业
| class | OCavg | OCmax | WMC |
|---|---|---|---|
| MainClass | 2.0 | 2.0 | 2.0 |
| expression.SumFunc | 5.0 | 5.0 | 5.0 |
| expression.key.KeyOfTrigo | 1.6666666666666667 | 3.0 | 5.0 |
| expression.key.KeyOfMulPart | 2.0 | 3.0 | 6.0 |
| expression.CustomFunc | 2.2 | 4.0 | 11.0 |
| expression.TrigoFunc | 1.7777777777777777 | 6.0 | 16.0 |
| expression.Monomial | 1.5714285714285714 | 5.0 | 22.0 |
| parser.Lexer | 2.875 | 9.0 | 23.0 |
| parser.Parser | 1.8823529411764706 | 7.0 | 32.0 |
| expression.Expression | 2.111111111111111 | 9.0 | 38.0 |
| expression.MulPart | 1.8333333333333333 | 6.0 | 44.0 |
| Total | 204.0 | ||
| Average | 1.9805825242718447 | 5.363636363636363 | 18.545454545454547 |
分析
从分析结果可以看到,SumFunc 类的复杂度较高,这是因为再 SumFunc 中,我把求和函数调用的过程全都集中在了一个方法当中,使得整个类的复杂度偏高。
三、测试方案
由于指导书中已经给出了很详细的表达式文法,因此可以采用递归的方式生成表达式,再利用 python 的 sympy 库来比对自己的输出是否正确。
在生成表达式的过程中,为了使其有较大的概率生成特殊的因子(比如 sin(0)),我先采用一个随机数决定是否生成特殊因子,再进一步采用随机数来生成因子。例如下面是我生成三角函数指数的代码,由于我做了平方和的化简,因此要使其有较大概率生成平方项,以测试我平方和化简的正确性。
if (Math.abs(random.nextInt()) % 2 == 0) {
sb.append("** 2");
} else {
sb.append(generateExponent());
}
四、bug 分析
1、自身 bug 分析
对常数的错误处理而产生的 bug
我在处理表达式时,一遇到 sin(0) 就将其转化为 0,而对于 cos(0),我在输出的时候才将其转化为 1,这就导致在合并平方和的时候,若遇到 cos(0)**2,会寻找是否有 sin(0)**2 与之配对,而 sin(0)**2 又被我转化成了零,因此就错误地使 cos(0)**2 与表达式中的任意常数项均能配对,从而使化简出错。
对于 bug 的修复,仅需对 cos(0) 采用与 sin(0) 相同的处理方式即可,即一遇到 cos(0) 就将其转化为 1。而对于其他的三角函数,我并没有采用特殊的处理方式,因此就不会再产生与常数配对的情况。
没有认真阅读指导书而产生的 bug
指导书中写道,0**0 等于 1,求和函数的下界可以大于上界,我由于没有注意到这两点而产生了 bug。
2、他人 bug 分析
- 字符串替换带来的 bug :暴力地将 x*1 替换为 x,i**2 替换时没有考虑到 i 可能为负数。
- 表达式化简考虑不全面。
- 采用 int 存储数字而造成溢出。
- 没有认真阅读指导书而产生 bug :0**0,sum 的上下界。
五、心得体会
1、面向对象与面向过程
pre 和 第一单元的学习让我慢慢体会到了面向对象与面向过程思维方式的不同。以前写程序的时候,我总是将一个问题分成若干个步骤,通过一步一步地完成每个步骤而解决这个问题。而在学习了面向对象之后,我拿到一个问题,首先考虑的是解决这个问题我需要哪些东西,各个东西需要有什么功能、属性,他们之间又该如何分工协作以解决这个问题。比如我需要写字,那么我需要有纸和笔,笔具有出墨的功能,纸具有粘墨的功能,他们共同协作以完成写字这件事。
2、架构设计
在第一单元的迭代开发中我也深刻体会到了好的架构带来的好处。好的架构易于拓展,当拿到一个新的需求,我们不需要对原有的代码做出大幅度的改动。同时好的架构也更容易 debug,若各个模块之间的耦合度比较低,那么我们就可以通过 print 的方式快速的定位到 bug 的位置。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号