暑假训练数论
斐波那契 https://www.cnblogs.com/Milkor/p/4734763.html
通项公式
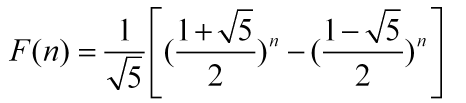求证过程就算了
斐波那契和矩阵的关系：
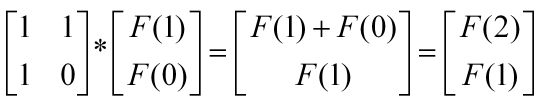
实现过程是根据快速幂改编的
void fen(ll r[][2],ll k[][2])//矩阵乘法 { ll ans[2][2]; ans[0][0]=(r[0][0]*k[0][0]%mod+r[0][1]*k[1][0]%mod)%mod; ans[0][1]=(r[0][0]*k[0][1]%mod+r[0][1]*k[1][1]%mod)%mod; ans[1][0]=(r[1][0]*k[0][0]%mod+r[1][1]*k[1][0]%mod)%mod; ans[1][1]=(r[1][0]*k[0][1]%mod+r[1][1]*k[1][1]%mod)%mod; r[0][0]=ans[0][0],r[0][1]=ans[0][1],r[1][0]=ans[1][0],r[1][1]=ans[1][1]; } ll fbnq(ll num) { if(num==0) return 0; ll k[2][2]={1,0,0,1}; ll r[2][2]={1,1,1,0}; while(num>1) { if(((num&1)!=0)) fen(k,r); fen(r,r);//思想可以参考快速幂 num>>=1; } fen(r,k); return r[0][1]; }
一些常用性质
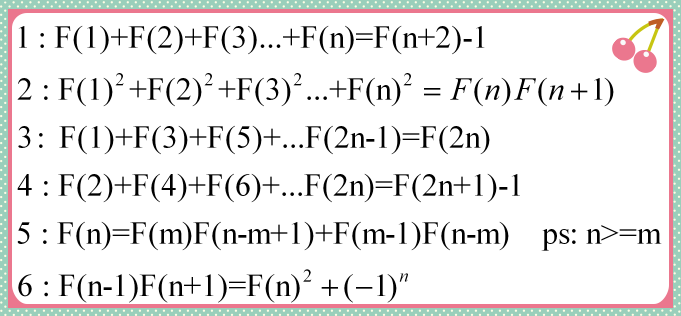
例题
(f[0]=0,f[1]=1;f[i] = f[i-1]+f[i-2](i>=2))的值全部给背了下来。
接下来，CodeStar决定要考考他，于是每问他一个数字，他就要把答案说出来，不过有的数字太长了。所以规定超过4位的只要说出前4位就可以了，可是CodeStar自己又记不住。于是他决定编写一个程序来测验zouyu说的是否正确。
Input输入若干数字n(0 <= n <= 100000000)，每个数字一行。读到文件尾。Output输出f[n]的前4个数字（若不足4个数字，就全部输出）。Sample Input
0 1 2 3 4 5 35 36 37 38 39 40
Sample Output
0 1 1 2 3 5 9227 1493 2415 3908 6324 1023
数字有点大，递推不行，可以运用公式，但要求前4位，可以
log10(10234432)=log10(1.0234432*10^7)=log10(1.0234432)+7;
log10(1.0234432)就是log10(10234432)的小数部分.
log10(1.0234432)=0.010063744
10^0.010063744=1.023443198
#include<iostream> #include<cmath> #include<string.h> using namespace std; int f[20]; int main() { int n; double s; f[0]=0,f[1]=1; for(int i=2;i<20;i++) f[i]=f[i-1]+f[i-2]; while(cin>>n) { if(n<20) { cout<<f[n]<<endl; continue; } s=log10(1.0/sqrt(5.0))+n*log10((1+sqrt(5.0))/2); s=s-(int)s; s=pow(10,s); while(s<1000) s*=10; cout<<(int)s<<endl; } }
InputThere is only one test case.
The first line contains single integer Q – the number of queries. (Q<=10^4)
Each line next will contain two integer L, R. (1<=L<=R<=10^12)OutputFor each query output one line.
Due to the final answer would be so large, please output the answer mod 1000000007.Sample Input
2 1 300 2 400
Sample Output
838985007 352105429
题意：sum[i]=fib[4*i-1] 给出L,R，求出中间的p[i]的和。
Sum[i]=Fib[3]+Fib[7]+......+Fib[4i-1]，
因为Fib[m+n-1]=Fib[m-1]*Fib[n-1]+Fib[m]*Fib[n]
所以Fib[4i-1]=Fib[2i+2i-1]=Fib[2i-1]*Fib[2i-1]+Fib[2i]*Fib[2i]
所以Sum[i]=Fib[1]*Fib[1]+Fib[2]*Fib[2]+......+Fib[2i]*Fib[2i]
又Fib[i]*Fib[i+1]+Fib[i+1]*Fib[i+1]=Fib[i+1]*Fib[i+2]
代入计算可得Sum[i]=Fib[2i]*Fib[2i+1]-Fib[0]*Fib[1]=Fib[2i]*Fib[2i+1]
最后发现Sum[i]只和fibonacci的两项有关。
关于fibonacci数列的一项可以构造矩阵在O(logn)时间内算出。
#include<iostream> #include<cstdio> #include<string.h> #include<algorithm> using namespace std; #define mod 1000000007 #define ll long long void fen(ll r[][2],ll k[][2]) { ll ans[2][2]; ans[0][0]=(r[0][0]*k[0][0]%mod+r[0][1]*k[1][0]%mod)%mod; ans[0][1]=(r[0][0]*k[0][1]%mod+r[0][1]*k[1][1]%mod)%mod; ans[1][0]=(r[1][0]*k[0][0]%mod+r[1][1]*k[1][0]%mod)%mod; ans[1][1]=(r[1][0]*k[0][1]%mod+r[1][1]*k[1][1]%mod)%mod; r[0][0]=ans[0][0],r[0][1]=ans[0][1],r[1][0]=ans[1][0],r[1][1]=ans[1][1]; } ll fbnq(ll num) { if(num==0) return 0; ll k[2][2]={1,0,0,1}; ll r[2][2]={1,1,1,0}; while(num>1) { if(((num&1)!=0)) fen(k,r); fen(r,r); num>>=1; } fen(r,k); return r[0][1]; } int main() { int t; cin>>t; while(t--) { ll l,r; ll sl=0,sr=0; cin>>l>>r; l--; sl=fbnq(2*l)*fbnq(2*l+1); sr=fbnq(2*r)*fbnq(2*r+1); cout<<((sr-sl)%mod+mod)%mod<<endl; } }
卡特兰数
出栈顺序：3 2 4 1 也是合法的，对于数字 3 而言，它后面比 3 小的数字有： 2 1，这个顺序是递减的；对于数字 2 而言，它后面的比它 小的数字只有 1，也算符合递减顺序；对于数字 4 而言，它后面的比它小的数字也只有1，因此也符合递减顺序。
出栈顺序：3 1 4 2 是不合法的，因为对于数字 3 而言，在3后面的比3小的数字有：1 2，这个顺序是一个递增的顺序(1-->2)。
然后T行，每行为一个数N(1<=N<=1000000)表示长方形的大小。Output 对于每组数据，输出符合题意的方案数。由于数字可能非常大，你只需要把最后的结果对1000000007取模即可。Sample Input
2 1 3Sample Output
Case #1: 1 Case #2: 5
数字应该是从小到大放置的，1肯定在左上角，所以1入栈，这时候我们放2，如果我们把2放在了1的下面就代表了1出栈，把2放在上面就代表了2也进栈（可以看一下hint中第二组样例提示），以此类推，这样去放数，正好就对应了上面一行入栈，下面一行出栈的情况，一共n行，对应上限为n的卡特兰数。
还有种想法
我们假设0代表这个数放在第一排，1代表这个数放在第二排，如果序列00001111
就是 1 2 3 4
5 6 7 8
序列01010101 就是 1 3 5 7
2 4 6 8
这个问题就转化成有几种满足题目条件的01序列，通过观察发现每个位置之前0的个数大于等于1的个数
如果把0看成入栈，1看成出栈,
这个问题变转化成n个数的入栈的出栈次序的种类数，也就是卡特兰数
h(n)=h(n-1)*(4*n-2)/(n+1);这里运用这个公式，但是要注意除法没有同余 要用逆元。
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> using namespace std; #define maxn 1000010 #define mod 1000000007 #define LL long long LL ktl[maxn],x,y; LL exgcd(LL a,LL b) { if(b == 0) { x = 1; y = 0; return a; } LL gcd = exgcd(b,a%b); LL tmp; tmp = x; x = y; y = tmp - a/b * y; return gcd; } LL yiyuan(int n) { LL gcd = exgcd(n,mod); if(gcd == 1) return (x%mod + mod) % mod; } void init() { memset(ktl,0,sizeof(ktl)); ktl[1] = 1; for(int i = 2; i <= maxn-10; i++) { ktl[i] = (ktl[i-1]*(4*i-2)%mod * yiyuan(i+1)) % mod; } } int main() { int t,n,ca = 0; init(); scanf("%d",&t); while(t--) { scanf("%d",&n); printf("Case #%d:\n",++ca); printf("%I64d\n",ktl[n]); } return 0; }
欧拉函数
转https://www.cnblogs.com/handsomecui/p/4755455.html
在数论中，对于正整数N,少于或等于N ([1,N]),且与N互质的正整数(包括1)的个数，记作φ(n)。
φ函数的值：
φ(x)=x(1-1/p(1))(1-1/p(2))(1-1/p(3))(1-1/p(4))…..(1-1/p(n)) 其中p(1),p(2)…p(n)为x
的所有质因数;x是正整数; φ(1)=1(唯一和1互质的数，且小于等于1)。注意：每种质因数只有一个。
例如:
φ(10)=10×(1-1/2)×(1-1/5)=4;
1 3 7 9
φ(30)=30×(1-1/2)×(1-1/3)×(1-1/5)=8;
φ(49)=49×(1-1/7)=42;
欧拉函数的性质：
(1) p^k型欧拉函数:
若N是质数p(即N=p), φ(n)= φ(p)=p-p^(k-1)=p-1。
若N是质数p的k次幂(即N=p^k)，φ(n)=p^k-p^(k-1)=(p-1)p^(k-1)。
(2)mn型欧拉函数
设n为正整数，以φ(n)表示不超过n且与n互素的正整数的个数，称为n的欧拉函数值。若m,n互质，φ(mn)=(m-1)(n-1)=φ(m)φ(n)。
(3)特殊性质:
若n为奇数时，φ(2n)=φ(n)。
对于任何两个互质 的正整数a,n(n>2)有:a^φ(n)=1 mod n (恒等于)此公式即 欧拉定理
当n=p 且 a与素数p互质(即:gcd(a,p)=1)则上式有: a^(p-1)=1 mod n (恒等于)此公式即 费马小定理
同余定理：
如果 a mod b = c 则有(a+kb) mod b =c(k为非0整数)
如果 a mod b = c 则有(ka) mod b =kc (k为正整数)
(a+b) mod c =((a mod c)+(b mod c )) mod c;
(a*b) mod c=((a mod c)*(b mod c)) mod c
欧拉函数模板
int phi(int n)//直接求 { int t=n; for(int i=2;i*i<=n;i++) { if(n%i==0) { t=t/i*(i-1); while(n%i==0) n/=i; } } if(n>1) t=t/n*(n-1); return t; } int p[1000001]; void init()//打表 { memset(p,0,sizeof(p)); p[1]=1; for(int i=2;i<1000000;i++) { if(p[i]==0) { for(int j=i;j<1000000;j+=i) { if(p[j]==0) p[j]=j; p[j]=p[j]/i*(i-1); } } } }
例题
For each N, output ,∑gcd(i, N) 1<=i <=N, a line
#include<iostream> #include<stdio.h> #define ll long long using namespace std; ll phi(int n) { ll res=n; for(ll i=2;i*i<=n;i++) { if(n%i==0) { res=res/i*(i-1); while(n%i==0)n/=i; } } if(n>1) res=res/n*(n-1); return res; } int main() { ll n; while(scanf("%lld",&n)!=EOF) { ll ans=0; for(ll i=1;i*i<=n;i++) { if(n%i==0) { ans+=i*phi(n/i);//phi(n/i)则为和n最大公约数为i的个数 if(i*i!=n) { ans+=n/i*phi(i); } } } cout<<ans<<endl; } return 0; }
快速乘法和快速幂
ll multi(ll a,ll b) { ll res=0; while(b) { if(b&1) res=(res+a)%p; a=(a+a)%p; b>>=1; } return res; } ll powmod(ll a,ll b) { ll res=1; while(b) { if(b&1) res=multi(res,a)%p; a=multi(a,a)%p; b>>=1; } return res; }
扩展欧几里德模板
ll ex_gcd(ll a,ll b,ll &x,ll &y) { if(b==0) { x=1; y=0; return a; } ll r=ex_gcd(b,a%b,y,x); y-=x*(a/b); return r; }
逆元模板
ll ex_gcd(ll a,ll b,ll &x,ll &y) { if(a==0&&b==0) return -1;//无最大公约数 if(b==0){ x=1; y=0; return a; } ll d=ex_gcd(b,a%b,y,x); y-=a/b*x; return d; } ll niyuan(ll a,ll n) { ll x,y; ll d=ex_gcd(a,n,x,y); if(d==1) return (x%n+n)%n; else return -1; }
