Spoj 2878 KNIGHTS - Knights of the Round Table | 双联通分量 二分图判定

题目链接

 

考虑建立原图的补图，即如果两个骑士不互相憎恨，就在他们之间连一条无向边。

显而易见的是，如果若干个骑士在同一个点数为奇数的环上时，他们就可以在一起开会。换句话说，如果一个骑士被一个奇环包含，那么他就一定可以去开会。

想到环，我们就可以考虑无向图的双联通分量。

当我们用Tarjan算法求出无向图上的双联通分量后再来考虑这一道题时，我们就可以得出两个结论：

1.如果两个骑士分别在两个不同的双联通分量里，那么他们就不可能在一起开会。

这一个结论是很明显的。因为将每个双联通分量缩点后，新图一定是一棵树，那么任意两个不同的双联通分量之间就不会存在环，连环都没有，就肯定不能在一起开会了。

2.如果在一个双联通分量里存在一个奇环，那么这一个双联通分量中的任意一个节点都至少会被一个奇环包含。

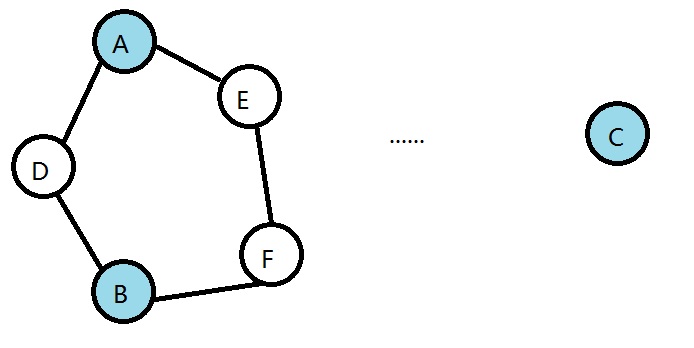
这一个证明起来也很容易。如图，节点A,B,C,D,E,F同属一个双联通分量，节点A,B,D,E,F构成了一个奇环。首先，对于奇环上的点，上述结论显然成立，我们要重点讨论的是奇环外的点，即节点C。此时，我们在这个环上取两个点A,B，那么，这一个环就相当于被分割成了两部分，一部分是D，另一部分是E,F。因为环的长度是奇数，所以这两部分的长度肯定是一奇一偶的。接下来，我们分别找一条从A到C的路径和一条从B到C的路径，且这两条路径在中途不相交，因为它们同属一个双联通分量，所以这样的两条路径一定存在。如果这两条路径的和为奇数的话，我们就拿这两条路径和环上偶数的那一部分接起来，否则就拿这两条路径和环上偶数的那一部分接起来。总之，无论怎么样，我们都能配出一个奇环将节点C包含。

 

 

有了这两条结论后，这道题做起来就很容易了。我们只需单独考虑每一个双联通分量，然后判断这一个双联通分量里是否有奇环即可，如果没有的话，这一个双联通分量里的骑士就都不能开会。那么应该如何判断是否有奇环呢？如果一个图里存在奇环，那它就一定不是一个二分图，否则它就一定是。也就是说，我们只要利用染色来判定某一个双联通分量是否为二分图即可。

 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
    using namespace std;
struct edge
{
    int last;
    int end;
}e[2000005];
    int ne=0,tot=0,cnt=0,top=0;
    int sta[1005],col[1005],dfn[1005],low[1005],note[1005];
    bool flag=false,mark[1005],book[1005],f[1005][1005];
    vector<int> dcc[1005];
void NewEdge(int u,int v)
{
    ne++;
    e[ne].last=note[u];
    e[ne].end=v;
    note[u]=ne;
}
void tarjan(int x)//求点双联通分量 
{
    dfn[x]=low[x]=++tot;
    sta[++top]=x;
    for(int i=note[x];i;i=e[i].last)
        if(!dfn[e[i].end])
        {
            tarjan(e[i].end);
            low[x]=min(low[x],low[e[i].end]);
            if(low[e[i].end]>=dfn[x]) 
            {
                cnt++;
                dcc[cnt].push_back(x);
                while(sta[top+1]!=e[i].end)
                    dcc[cnt].push_back(sta[top--]);
            }
        }
        else low[x]=min(low[x],dfn[e[i].end]);
}
void dfs(int x)//二分图判定 
{
    if(flag) return;
    for(int i=note[x];i;i=e[i].last) 
    {
        if(!mark[e[i].end]) continue;
        if(!col[e[i].end])
            col[e[i].end]=(col[x]==1)?2:1,dfs(e[i].end);
        else if(col[e[i].end]==col[x]) {flag=true;break;}
    }
}
int main()
{
    for(;;)
    {
        int n=0,m=0;
        scanf("%d%d",&n,&m);
        if(n==0&&m==0) break;    
        memset(f,0,sizeof(f));
        for(int i=1;i<=m;i++)
        {
            int x=0,y=0;
            scanf("%d%d",&x,&y);
            f[x][y]=f[y][x]=true;
        }
        ne=0,memset(note,0,sizeof(note));
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                if(i!=j&&!f[i][j]) NewEdge(i,j);
        tot=0,top=0,cnt=0;
        memset(dfn,0,sizeof(dfn));
        memset(sta,0,sizeof(sta));
        for(int i=1;i<=n;i++) dcc[i].clear();
        for(int i=1;i<=n;i++)
            if(!dfn[i]) tarjan(i);
        memset(book,0,sizeof(book));
        for(int i=1;i<=cnt;i++) 
        {
            int len=dcc[i].size();
            for(int j=0;j<len;j++)    mark[dcc[i][j]]=true;
            flag=false,col[dcc[i][0]]=1,dfs(dcc[i][0]);
            if(flag)
                for(int j=0;j<len;j++) book[dcc[i][j]]=true;
            for(int j=0;j<len;j++)
                mark[dcc[i][j]]=false,col[dcc[i][j]]=0;
        }
        int ans=0;
        for(int i=1;i<=n;i++)
            if(!book[i]) ans++;
        printf("%d\n",ans);
    }
    return 0;
}