PAT 1018 Public Bike Management (dijkstra)

题意

There is a public bike service in Hangzhou City which provides great convenience to the tourists from all over the world. One may rent a bike at any station and return it to any other stations in the city.

The Public Bike Management Center (PBMC) keeps monitoring the real-time capacity of all the stations. A station is said to be in perfect condition if it is exactly half-full. If a station is full or empty, PBMC will collect or send bikes to adjust the condition of that station to perfect. And more, all the stations on the way will be adjusted as well.

When a problem station is reported, PBMC will always choose the shortest path to reach that station. If there are more than one shortest path, the one that requires the least number of bikes sent from PBMC will be chosen.

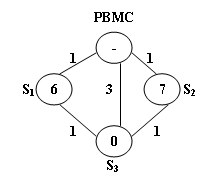
The above figure illustrates an example. The stations are represented by vertices and the roads correspond to the edges. The number on an edge is the time taken to reach one end station from another. The number written inside a vertex S is the current number of bikes stored at S. Given that the maximum capacity of each station is 10. To solve the problem at S3, we have 2 different shortest paths:

1. PBMC -> S1 -> S3. In this case, 4 bikes must be sent from PBMC, because we can collect 1 bike from S1 and then take 5 bikes to S3, so that both stations will be in perfect conditions.
2. PBMC -> S2 -> S3. This path requires the same time as path 1, but only 3 bikes sent from PBMC and hence is the one that will be chosen.

Input Specification:

Each input file contains one test case. For each case, the first line contains 4 numbers: Cma**x (≤100), always an even number, is the maximum capacity of each station; N (≤500), the total number of stations; S**p, the index of the problem station (the stations are numbered from 1 to N, and PBMC is represented by the vertex 0); and M, the number of roads. The second line contains N non-negative numbers C**i (i=1,⋯,N) where each C**i is the current number of bikes at S**i respectively. Then M lines follow, each contains 3 numbers: S**i, S**j, and Tij which describe the time Tij taken to move betwen stations S**i and S**j. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print your results in one line. First output the number of bikes that PBMC must send. Then after one space, output the path in the format: 0−>S1−>⋯−>S**p. Finally after another space, output the number of bikes that we must take back to PBMC after the condition of S**p is adjusted to perfect.

Note that if such a path is not unique, output the one that requires minimum number of bikes that we must take back to PBMC. The judge's data guarantee that such a path is unique.

Sample Input:

10 3 3 5
6 7 0
0 1 1
0 2 1
0 3 3
1 3 1
2 3 1

Sample Output:

3 0->2->3 0

思路

先跑一边dijkstra求出0->S的最短路径。

由于此种方法，求得的路径是逆向的，因此要写个函数将其逆置。

然后有了路径后，从0开始逐步向S递归，求得最佳路径。在编写这个函数的时候，要注意理清从PBMC带的车的数量和带回PBMC的数量。

思路可能还可以在优化，因此最后一组数据没有过，只拿到了29分

代码

#include <stdio.h>
#include <string>
#include <stdlib.h>
#include <iostream>
#include <vector>
#include <string.h>
#include <algorithm>
#include <cmath>
#include <map>
#include <queue>
#include <functional>
#include <limits.h> 
using namespace std;
int C, N, S, M;
int num[500 + 10]; //记录每个车站的车辆 
int maze[500 + 10][500 + 10]; //记录图 
vector<int> path[500 + 10]; // 记录逆向的路径 S->...->0 
vector<int> path2[500 + 10]; // 记录正向路径 0->...->S 
int bto = INT_MAX, bfrom = INT_MAX;	//分别记录最小的带去的车辆，和 最小的带走车辆 
vector<int> ans; // 记录最佳路径 

//用于将路径反转 
void get_rode(int me, int pre){
	if(me == 0)	path[me].clear();
	for(int i = 0; i < path[me].size(); i++){
		get_rode(path[me][i], me);
	}
	path2[me].push_back(pre);
}

//dfs求最佳路径 
void dfs(int p, int to, int from, vector<int>& anst){
	if(p == S){
		// 更新路径 
		if(to < bto){
			bto = to;
			bfrom = from;
			ans = anst;
		}
		else if(to == bto && from < bfrom){
			bfrom = from;
			ans = anst;
		}
	}
	for(int i = 0; i < path2[p].size(); i++){
		anst.push_back(path2[p][i]);
		// 足够 
		if(from + num[path2[p][i]] > C / 2)	dfs(path2[p][i], to, num[path2[p][i]] -  C / 2 + from, anst);
		// 不够 
		else dfs(path2[p][i], to + C / 2 - num[path2[p][i]] - from, 0, anst);
		anst.pop_back();
	}
}
//求最短路径(逆向) 
void dijkstra(int cc) {
	int dist[500 + 10];
    for (int i = 1; i <= N; i++){
    	dist[i] = maze[i][cc];
    	path[i].push_back(cc);
	}   
    dist[cc] = 0;
	bool vis[500 + 10];
    memset(vis, 0, sizeof(vis));
    vis[cc] = 1;
    for (int i = 0; i <= N; i++) {
        int mark = -1, mindis = 185273099;
        for (int j = 0; j <= N; j++) {
            if (!vis[j] && dist[j] < mindis) {
                mindis = dist[j];
                mark = j;
            }
        }
        vis[mark] = 1;
        for (int j = 0; j <= N; j++) {
            if (!vis[j]) {
            	if(dist[j] > dist[mark] + maze[mark][j]){
            		path[j].clear();
            		path[j].push_back(mark);
            		dist[j] = dist[mark] + maze[mark][j];
				}
				else if(dist[j] == dist[mark] + maze[mark][j]){
					path[j].push_back(mark);
				}
            }
        }
    }
}


int main() {
	cin >> C >> N >> S >> M;
	for(int i = 1; i <= N; i++){
		cin >> num[i];
	}
	int s, e, d;
	memset(maze, 11, sizeof(maze)); // 185273099
	for(int i = 1; i <= M; i++){
		cin >> s >> e >> d;
		maze[s][e] = d;
		maze[e][s] = d;
	}
	dijkstra(0);
	for(int i = 0; i < path[S].size(); i++){
    	get_rode(path[S][i], S);
	}
	vector<int> anst;
	anst.push_back(0);
	dfs(0, 0, 0, anst);
	cout << bto << " ";
	for(int i = 0; i < ans.size(); i++){
		if(i)	cout << "->" ;
		cout << ans[i];
	}
	cout << " " << bfrom << endl;
	return 0; 
}