01背包 完全背包 算法解析

01背包问题

问题描述

　有n种物品，每种只有一个，第 i 种 物品的体积为V_i ，重量为 W_i。选一些物品装到一个容量为C的背包，使得总体积不超C的情况下，重量尽量大。

问题分析

这个问题可以把每一件物品视作一次决策，每次决策只有选与不选两种选择。

我们设d[ i ][ j ]为第1件物品到第 i 件物品，放到载重为 j 的背包中的最大价值。

因此状态转移方程为

\[d[i][j] = \max (d[i - 1][j],d[i - 1][j - w[i]] + v[i])\]

我们可以写出代码

for (int i = 1; i <= n; i++) {
	for (int j = 0; j <= c; j++) {
		d[i][j] = (i == 1 ? 0 : d[i - 1][j]);
		if (j >= W[i])
				d[i][j] = max(d[i][j], d[i - 1][j - W[i]] + V[i]);
	}
}

那么我这个算法还可以在空间复杂度上优化一下吗？如果我们能把数组d改为一维数组，那肯定再好不过了。

但是要保证，每一阶段的决策，我们要在修改上一阶段的值后，不在使用她的值。

我们可以用一个样例运行一下这个代码。

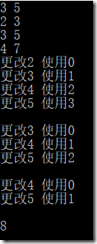
3 5
2 3
3 5
4 7

for (int i = 1; i <= n; i++) {
	for (int j = 0; j <= c; j++) {
		d[i][j] = (i == 1 ? 0 : d[i - 1][j]);
		if (j >= W[i]) {
			d[i][j] = max(d[i][j], d[i - 1][j - W[i]] + V[i]);
			cout << "更改d" << j << " 使用" << j - W[i] << endl;
		}
	}
	cout << endl;
}

我们发现我们当我们用上一个阶段来修改当前阶段的值时，上述算法，会出现“交叉”的情况。

比如我们修改了d[i][2]，但是第七行我们就用到了，d[i-1][2]，因此如果我们想把d设为一维数组，这样得出的答案肯定错的，因为这时候的d[2]已经不是上一个阶段的d[2]了。

如果我们把第二层循环的循环方向修改一下，是不是会有所改善？

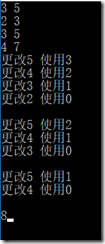
for (int i = 1; i <= n; i++) {
	for (int j = c; j >= 0; j--) {
		d[i][j] = (i == 1 ? 0 : d[i - 1][j]);
		if (j >= W[i]) {
			d[i][j] = max(d[i][j], d[i - 1][j - W[i]] + V[i]);
			cout << "更改" << j << " 使用" << j - W[i] << endl;
		}
	}
	cout << endl;
}

这一次打印的结果，没有出现刚才那种“交叉”情况（使用前，修改了对应标号的值）。

最终经过空间优化后的算法

for (int i = 1; i <= n; i++) {
	for (int j = c; j >= 0; j--) {
		if (j >= W[i])
			d[j] = max(d[j], d[j - W[i]] + V[i]);
	}
}

完全背包问题

问题描述

有n种物品，每种有无穷多个，第 i 种 物品的体积为V_i ，重量为 W_i。选一些物品装到一个容量为C的背包，使得总体积不超C的情况下，重量尽量大。

题目分析

01背包问题中，我们所作的决定只是拿与不拿的选择，而完全背包问题，我们还要考虑拿几个的问题。

\[d[i][j] = \max (d[i - 1][j],d[i - 1][j - k*w[i]] + k*v[i])\]

for (int i = 1; i <= n; i++) {
	for (int j = c; j >= 0; j--) {
		d[i][j] = (i == 1 ? 0 : d[i - 1][j]);
		for (int k = 0; k * W[i] <= j; k++) {
			d[i][j] = max(d[i][j], d[i - 1][j - k * W[i]] + k * V[i]);
		}
	}
}

那我们还能像01背包问题一样优化吗，当然可以。

for (int i = 1; i <= n; i++) {
	for (int j = W[i]; j <= c; j++) {
		d[j] = max(d[j], d[j - W[i]] + V[i]);
	}
}

那么现在我们可以发现，内层循环是顺序的，而01背包问题是逆序的，这两者有什么区别和联系吗？

01背包问题，我们需要用上一阶段的值，来更新本阶段的值，而背包问题是重量小的状态来更新质量大的状态(因为j-w[i])，因此逆序保证了更新的过程中，不会更改接下来要用到的上一阶段的值。

完全背包问题，我们需要用本阶段的值，来更新本阶段的值，因此要顺序。