最长上升子序列(LIS)n2 nlogn算法解析
题目描述
给定一个数列,包含N个整数,求这个序列的最长上升子序列。
例如 2 5 3 4 1 7 6 最长上升子序列为 4.
1.O(n2)算法解析
看到这个题,大家的直觉肯定都是要用动态规划来做,那么我们先设立一个数组。
设d[ i ]为以a[ i ]为结尾的最大子序列的长度
有了这个后,我们可以很容易的写出状态转移方程:
d[ i ] = max(d[ i ] , d[ j ] + 1) 若 j < i 且 a[ i ] > a[ j ]

#include <stdio.h> #include <iostream> #include <algorithm> using namespace std; #define N 1000 int d[N];//表示以a[i]结尾的最大长度 int a[N]; int main() { for (int i = 0; i < 7; i++) { cin >> a[i]; } d[0] = 1; for (int i = 1; i < 7; i++) { d[i] = 1; for (int j = 0; j < i; j++) { if (a[i] > a[j]) d[i] = max(d[j] + 1, d[i]); } } int maxt = -1; for (int i = 0; i < 7; i++) { maxt = max(d[i], maxt); } cout << maxt << endl; return 0; }
2.O(ologn)算法解析
首先我们给数组d换一种含义,设d[ i ] 为 长度为 i 的子序列的最后一个元素的值。
我们要做的就是,依次把每一个元素插到他合适的位置上去。
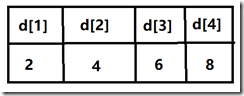
例如现在的数组d为
这时我们要处理一个元素,假设值为5,那我们应该放到哪里?
这里面长度为2的子序列最后一个长度为4,5>4,因此我们可以把5放到d[3]中。
但是把6换成5有什么意义呢?
显然,序列元素有限的情况下,子序列的末尾元素越小,越有利于我们向后添加元素(增大其长度)。
这句话就是解决问题的关键。
因此,处理每一个元素的时候,我们只需要把元素填入第一个大于这个元素值的d[ i ]中就好。
通过简单的分析,我们很容易知道数组d是个递增的数组,因此解决上面这个问题,我们采用二分查找,写一个find()函数,返回第一个大于该元素值 t 的数组d元素的下标。

#include <stdio.h> #include <iostream> #include <algorithm> using namespace std; #define N 1000 int d[N]; int a[N]; int find(int l, int r, int x) {//寻找数组d中第一个大于x的元素的下标 while (l <= r) { int mid = (l + r) / 2; if (d[mid] < x) { l = mid + 1; } else { r = mid - 1; } } return l; } int main() { for (int i = 0; i < 7; i++) { cin >> a[i]; } d[0] = -0x3f3f3f3f; int len = 1; for (int i = 1; i < 7; i++) { if (a[i] > d[len]) { d[++len] = a[i]; } else { int k = find(1, len, a[i]); d[k] = a[i]; } } cout << len; return 0; }