WUSTOJ 1325: Distance（Java）坐标计算

题目链接：1325: Distance

Description

There is a battle field. It is a square with the side length 100 miles, and unfortunately we have two comrades who get hurt still in the battle field. They are in different positions. You have to save them. Now I give you the positions of them, and you should choose a straight way and drive a car to get them. Of course you should cross the battle field, since it is dangerous, you want to leave it as quickly as you can!

有一个战场。这是一个边长100英里的正方形，不幸的是我们还有两个同志在战场上受伤。他们处于不同的位置。你必须拯救他们。现在我给你它们的位置，你应该选择一条直线，然后开车去取它们。当然你应该穿过战场，因为它很危险，你想尽快离开它!

Input

There are many test cases. Each test case contains four floating number, indicating the two comrades’ positions (x1,y1), (x2,y2).
Proceed to the end of file.

有许多测试用例。每个测试用例包含四个浮点数，表示两个同志的位置 (x1, y1)， (x2, y2) 。
继续到文件末尾。

Output

you should output the mileage which you drive in the battle field. The result should be accurate up to 2 decimals.

你应该输出你在战场上行驶的里程。结果应该精确到小数点后两位。

Sample Input

1.0 2.0 3.0 4.0
15.0 23.0 46.5 7.0
0.0 0.0 100.0 0.0
100.0 0.0 100.0 100.0
0.0 0.0 100.0 100.0
0.0 100.0 100.0 0.0
20.0 5.0 40.0 20.0
30.0 30.0 80.0 90.0
20.0 12.0 40.0 34.0
30.0 80.0 70.0 20.0
40.0 70.0 80.0 30.0
40.0 75.0 60.0 50.0
20.0 15.0 40.0 10.0
20.0 70.0 50.0 85.0
10.0 44.0 30.0 52.0

Sample Output

140.01
67.61
100.00
100.00
141.42
141.42
108.33
130.17
135.15
120.19
127.28
128.06
82.46
89.44
107.70

HINT

The battle field is a square local at (0,0),(0, 100),(100,0),(100,100).

战场是一个位于 (0, 0)，(0, 100)，(100, 0)，(100, 100) 的正方形。

分析💬

题目不难，读懂题目，细心编码一般都能做出来。

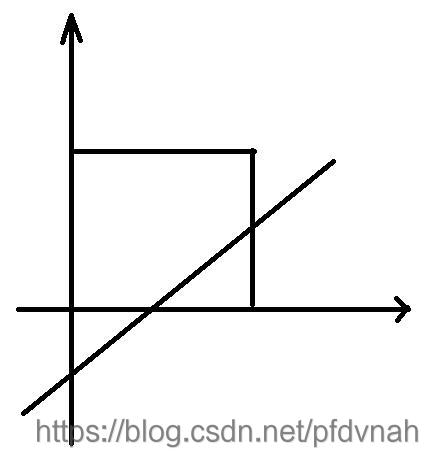
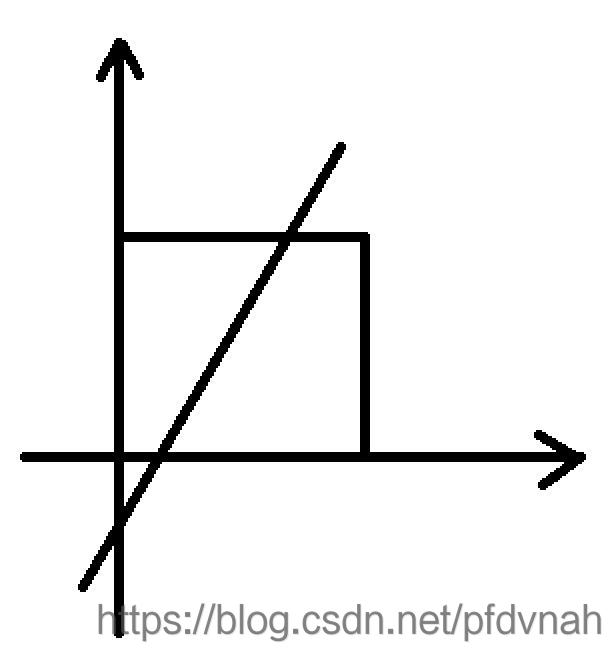
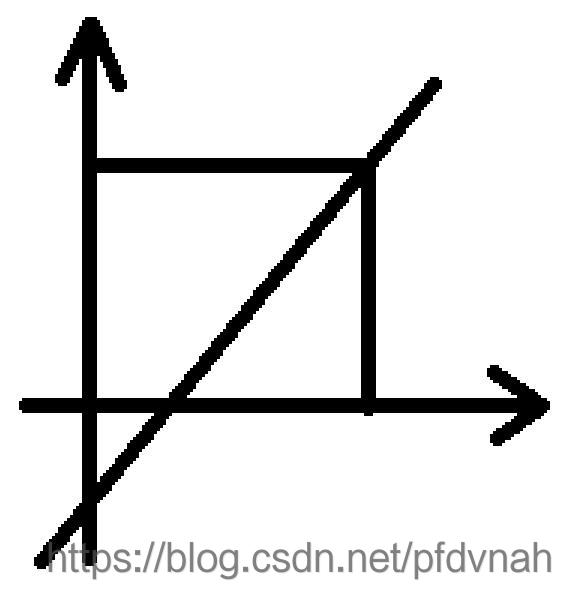
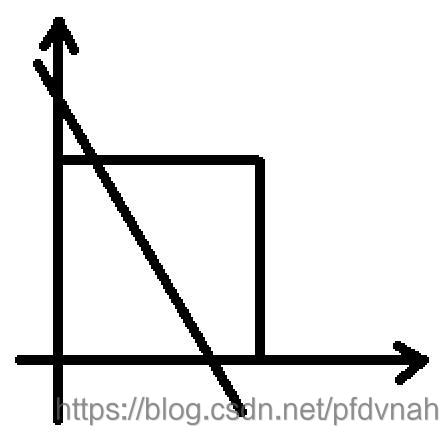
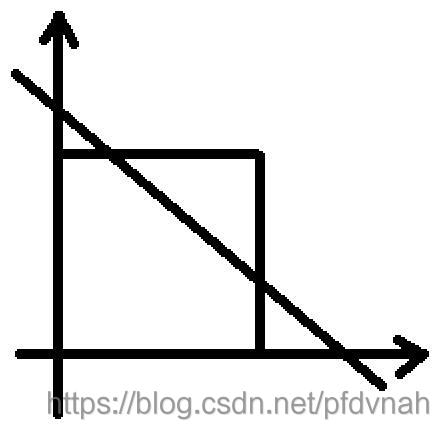
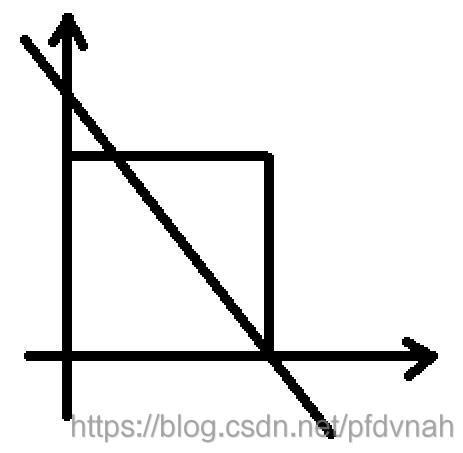
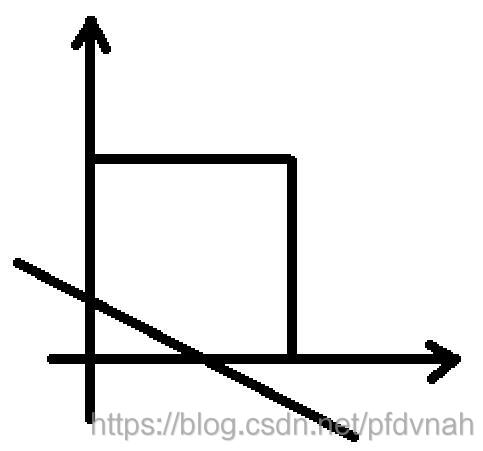
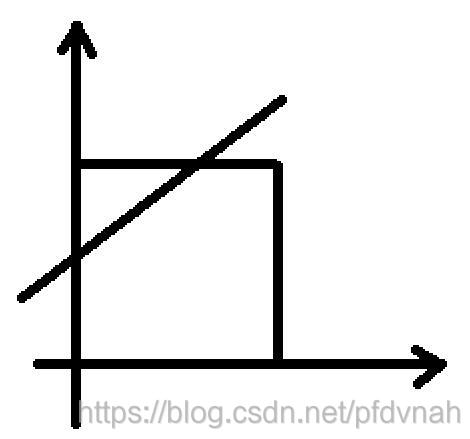
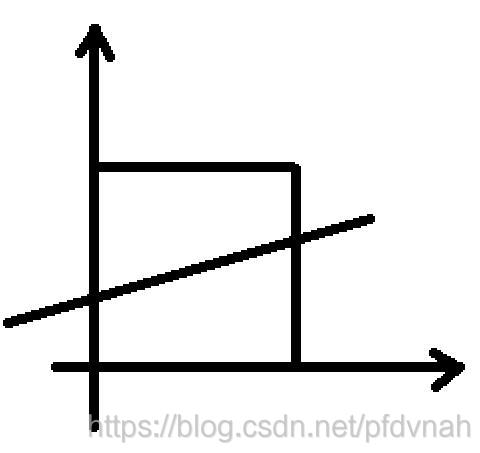
给你一个100×100的正方形，放在坐标系的第一维的紧贴坐标轴的位置。

正方形内（包括边框）有两个坐标不同的点。将两个点连成一条直线。直线与正方形边框相交于两个点 (m1, n1)，(m2, n2) ，计算两点的距离。保留两位小数。

代码💻

/**
 * Time 781ms
 * @author wowpH
 * @version 1.2
 * @date 2019年6月26日上午10:48:04
 * Environment:	Windows 10
 * IDE Version:	Eclipse 2019-3
 * JDK Version:	JDK1.8.0_112
 */

import java.io.InputStreamReader;
import java.util.Scanner;

public class Main {
	public Main() {
		Scanner sc = new Scanner(new InputStreamReader(System.in));
		while (sc.hasNext()) {
			double x1 = sc.nextDouble();
			double y1 = sc.nextDouble();
			double x2 = sc.nextDouble();
			double y2 = sc.nextDouble();
			System.out.printf("%.2f\n", solve(x1, y1, x2, y2));
		}
		sc.close();
	}

	private double solve(double x1, double y1, double x2, double y2) {
		if (x1 == x2 || y1 == y2) {	// 斜率不存在或斜率为0
			return 100;
		}
		// 方程y=ax+b
		double a = (y1 - y2) / (x1 - x2);// 斜率
		double b = y1 - a * x1;		// 与y轴交点，即一般形式的常数项
		double m1, n1, m2, n2;		// 直线与战场四个边的两个交点
		if (b < 0) {
			m1 = -b / a;			// 与x轴交点的横坐标
			n1 = 0;
			if (a < (100 / (100 - m1))) {
				m2 = 100;
				n2 = a * 100 + b;	// 与线段x=100交点的纵坐标
			} else if (a > (100 / (100 - m1))) {
				m2 = (100 - b) / a;	// 与线段y=100交点的横坐标
				n2 = 100;
			} else {
				m2 = n2 = 100;		// 顶点
			}
		} else if (b > 100) {
			m1 = (100 - b) / a;		// 与线段y=100交点的横坐标
			n1 = 100;
			if (a < (100 / (m1 - 100))) {
				m2 = -b / a;		// 与x轴交点的横坐标
				n2 = 0;
			} else if (a > (100 / (m1 - 100))) {
				m2 = 100;
				n2 = a * 100 + b;	// 与线段x=100交点的纵坐标
			} else {
				m2 = 100;			// 顶点
				n2 = 0;
			}
		} else {
			m1 = 0;
			n1 = b;
			if (a < (-b / 100)) {
				m2 = -b / a;		// 与x轴交点的横坐标
				n2 = 0;
			} else if (a > ((100 - b) / 100)) {
				m2 = (100 - b) / a;	// 与线段y=100交点的横坐标
				n2 = 100;
			} else {
				m2 = 100;
				n2 = a * 100 + b;	// 与线段x=100交点的纵坐标
			}
		}
		return Math.sqrt((m1 - m2) * (m1 - m2) + (n1 - n2) * (n1 - n2));
	}

	public static void main(String[] args) {
		new Main();
	}
}