games101_Homework1

　　本次作业的任务是填写一个旋转矩阵和一个透视投影矩阵。给定三维下三个 点 v0(2.0, 0.0, −2.0), v1(0.0, 2.0, −2.0), v2(−2.0, 0.0, −2.0), 你需要将这三个点的坐 标变换为屏幕坐标，并在屏幕上绘制出对应的线框三角形 (在代码框架中，我们 已经提供了 draw_triangle 函数，所以你只需要去构建变换矩阵即可)。简而言 之，我们需要进行模型、视图、投影、视口等变换来将三角形显示在屏幕上。在 提供的代码框架中，我们留下了模型变换和投影变换的部分给你去完成。

作业解答：

　　作业1：get_model_matrix(float rotation_angle): 逐个元素地构建模型变换矩 阵并返回该矩阵。在此函数中，你只需要实现三维中绕 z 轴旋转的变换矩阵， 而不用处理平移与缩放。该项只要求我们传入一个旋转角度然后返回一个旋转矩阵即可。(很简单)

Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
    Eigen::Matrix4f model = Eigen::Matrix4f::Identity();

    // TODO: Implement this function
    // Create the model matrix for rotating the triangle around the Z axis.
    // Then return it.

    // Rz matrix is (cosa, -sina, 0, 0)(sina, cosa, 0, 0)(0, 0, 1, 0)(0, 0, 0, 1)
    Eigen::Matrix4f Rz;
    Rz << cos(rotation_angle / 180.0 * MY_PI), -sin(rotation_angle / 180.0 * MY_PI), 0, 0,
          sin(rotation_angle / 180.0 * MY_PI),  cos(rotation_angle / 180.0 * MY_PI), 0, 0,
          0, 0, 1, 0,
          0, 0, 0, 1;

    return Rz * model;
}

　　作业2：get_projection_matrix(float eye_fov, float aspect_ratio, float zNear, float zFar): 使用给定的参数逐个元素地构建透视投影矩阵并返回 该矩阵。该项要求通过已知条件写出投影矩阵，这个需要用到L4、L5中提到的知识，即MVP变换。

Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,
                                      float zNear, float zFar)
{
    // Students will implement this function

    Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();

    // TODO: Implement this function
    // Create the projection matrix for the given parameters.
    // Then return it.

    // Get t、r、l、b by eye_fov and aspect_ration
    float t = abs(zNear) * tanf(eye_fov / 2);     // tan需传入角度，tanf传入一个float弧度返回一个float,此处fov/2为弧度值
    float r = t * aspect_ratio;
    float l = -r;
    float b = -t;

    // Create the perspective projection matrix Mpo
    Eigen::Matrix4f Mpo = Eigen::Matrix4f::Identity();;
    Mpo << zNear, 0, 0, 0,
           0, zNear, 0, 0,
           0, 0, zNear + zFar, -(zFar * zFar),
           0, 0, 1, 0;
    
    // Create the orthographic projection matrix Mor
    Eigen::Matrix4f MorTran = Eigen::Matrix4f::Identity();    //Mor平移矩阵
    MorTran << 1, 0, 0, -((l + r) / 2),
               0, 1, 0, -((t + b) / 2),
               0, 0, 1, -((zNear + zFar) / 2),
               0, 0, 0, 1;

    Eigen::Matrix4f MorScal = Eigen::Matrix4f::Identity();    //Mor大小变换矩阵
    MorScal << 2 / (r - l), 0, 0, 0,                          //Notice: t\r\l\b need be float        
               0, 2 / (t - b), 0, 0,    
               0, 0, 2 / (zNear - zFar), 0,
               0, 0, 0, 1;

    projection = MorScal * MorTran * Mpo * projection;
    return projection;
}

　　附加作业：在 main.cpp 中构造一个函数，该函数的作用是得到绕任意 过原点的轴的旋转变换矩阵。 Eigen::Matrix4f get_rotation(Vector3f axis, float angle) 。直接使用罗德里格斯公式返回一个旋转矩阵。

Eigen::Matrix4f get_rotation(Vector3f axis, float angle){
    //R1 = cosa * I
    Eigen::Matrix3f I = Eigen::Matrix3f::Identity();
    Eigen::Matrix3f R1 = cosf(angle) * I;
    
    //R2 = (1 - cosa) * n*nT 即 （1 - cosa）* (a[0], a[1], a[2])T * (a[0], a[1], a[2])
    Eigen::Matrix3f R2;
    R2 << axis[0] * axis[0], axis[0] * axis[1], axis[0] * axis[2],
          axis[1] * axis[0], axis[1] * axis[1], axis[1] * axis[2],
          axis[2] * axis[0], axis[2] * axis[1], axis[2] * axis[2];
    R2 = (1 - cosf(angle)) * R2;

    //R3 = sina * (0, -nz, ny)(nz, 0, -nx)(-ny, nx, 0)
    Eigen::Matrix3f R3;
    R3 << 0, -axis[2], axis[1],
          axis[2], 0, -axis[0],
          -axis[1], axis[0], 0;
    R3 = sinf(angle) * R3;

    Eigen::Matrix3f R = R1 + R2 + R3;
    Eigen::Matrix4f Res;
    Res << R(0,0), R(0,1), R(0,2), 0,
           R(1,0), R(1,1), R(1,2), 0,
           R(2,0), R(2,1), R(2,2), 0,
           0, 0, 0, 1;
    return Res;
}

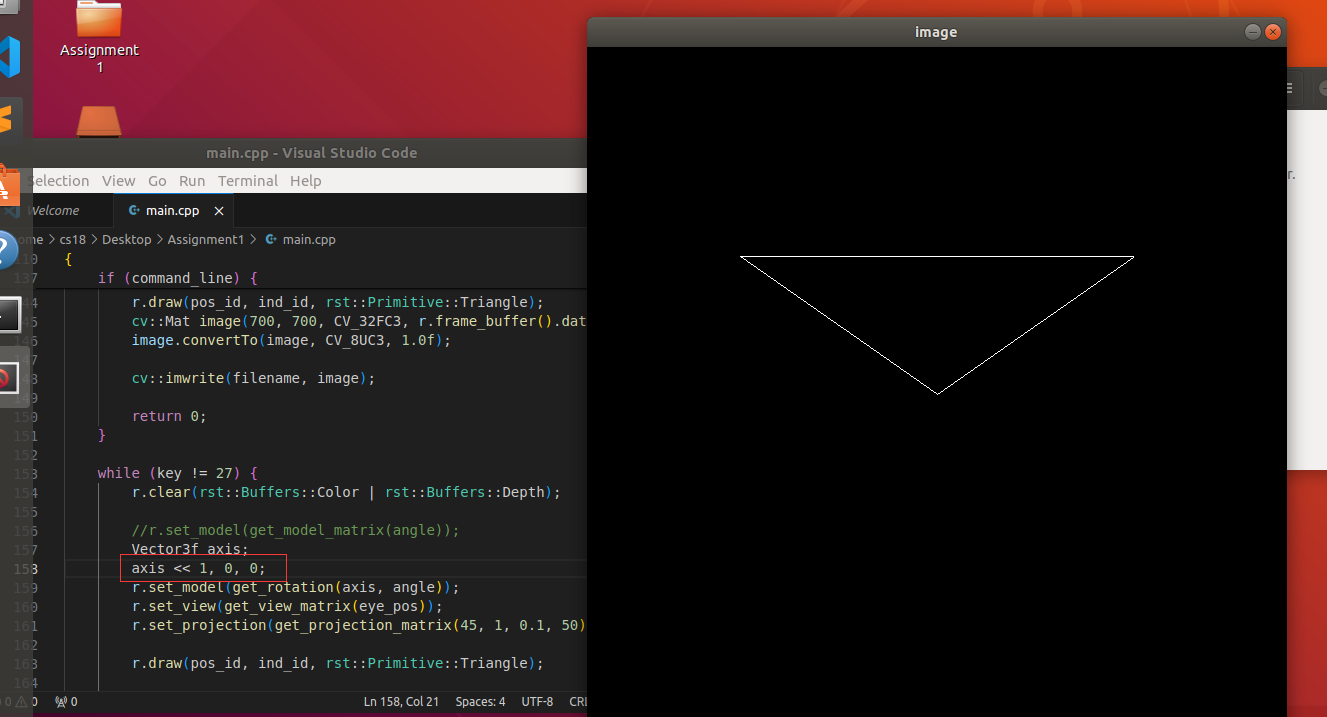
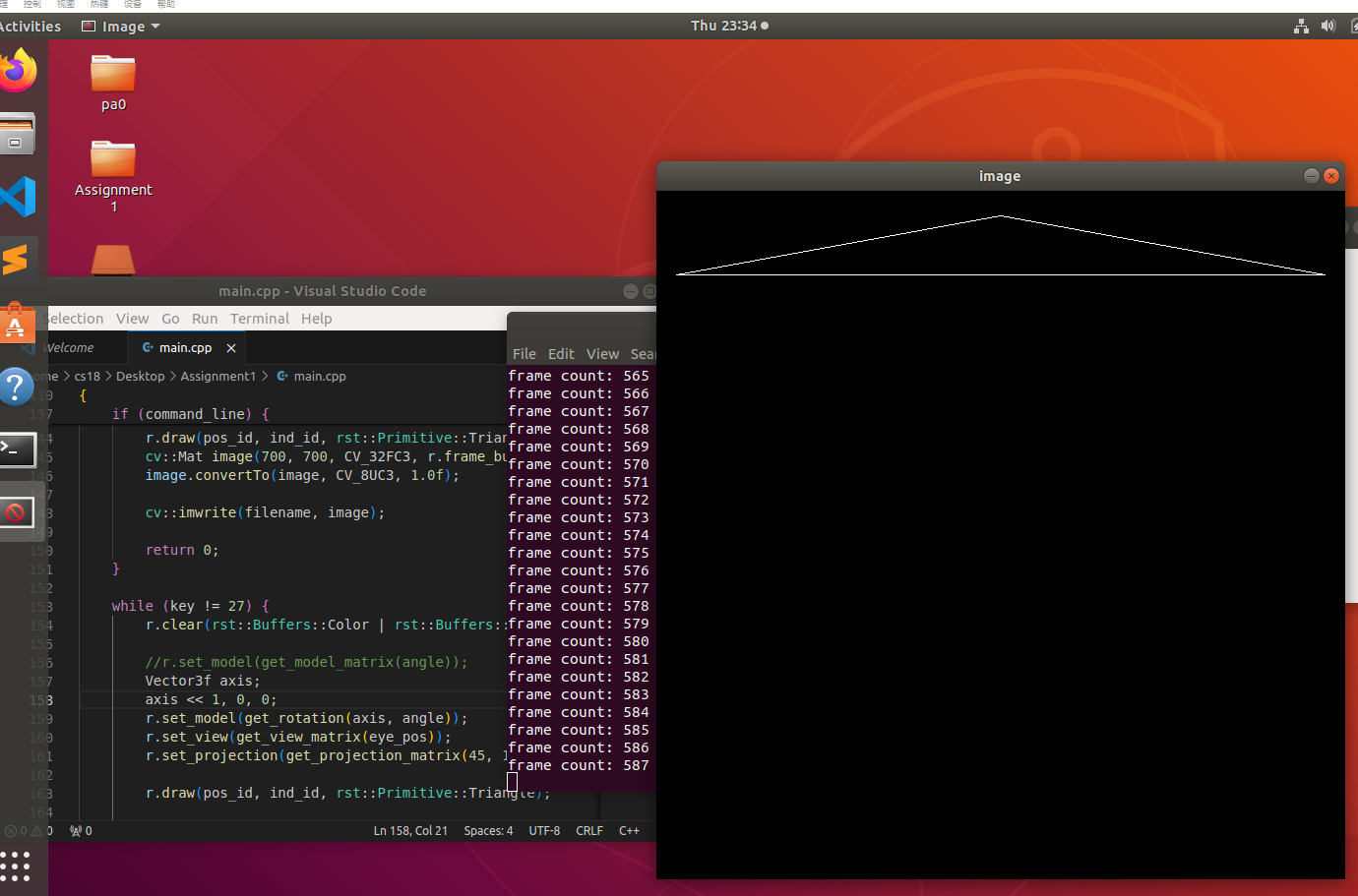
这里贴出绕x轴旋转效果