陌上花开，可缓缓归矣

陌上花开，可缓缓归矣（三维偏序）

其实是想复习树状数组和归并排序

cdq分治noip考完再说

一、归并排序（merge sort）

采用分治策略，分而治之，直接上原理图

 

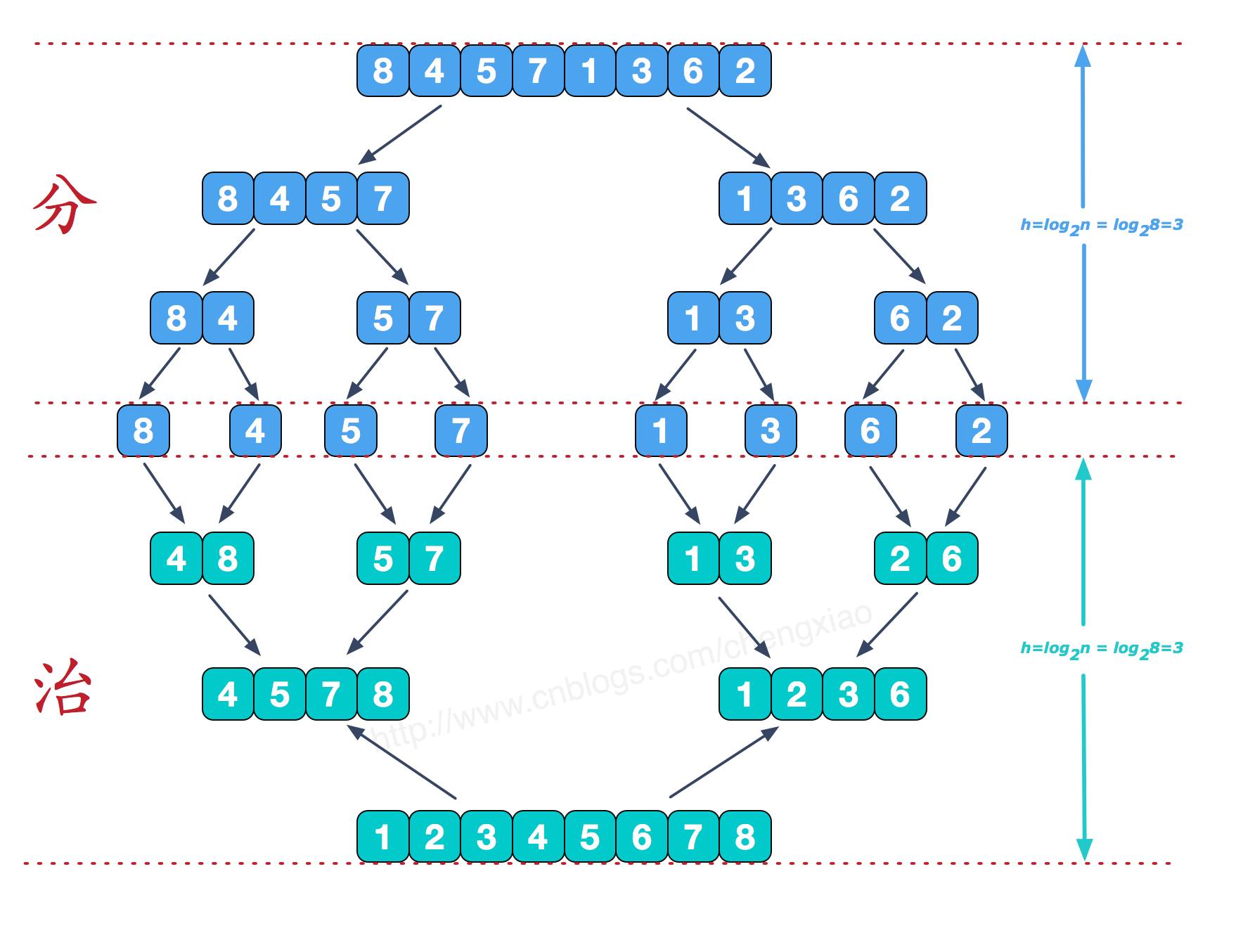
看上去像个完全二叉树，所以递归解决，复l杂度nlog₂n

递归分到最后，只有一个元素显然是有序的，这时候再进行二路归并，具体如下图

 

 

 

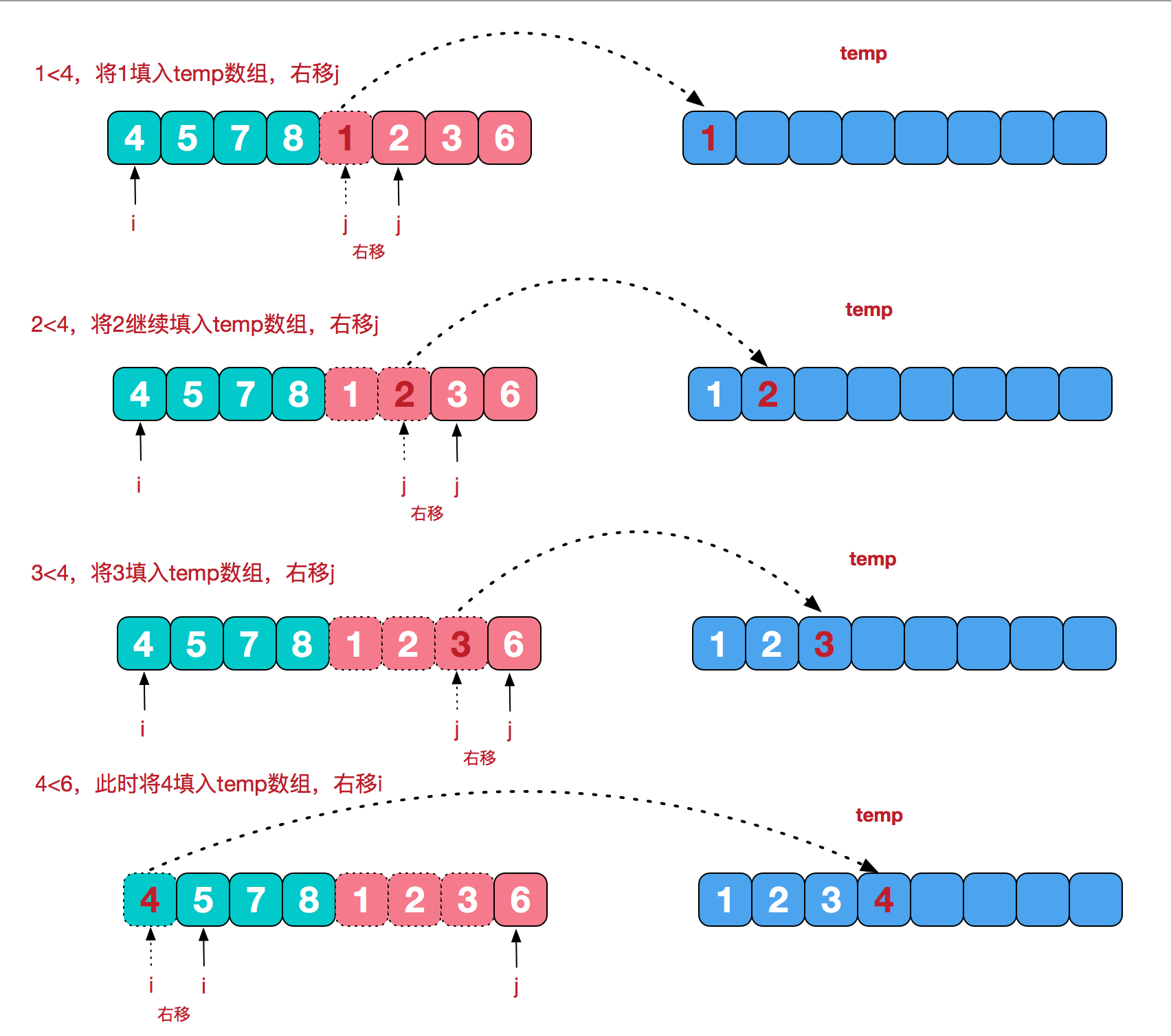
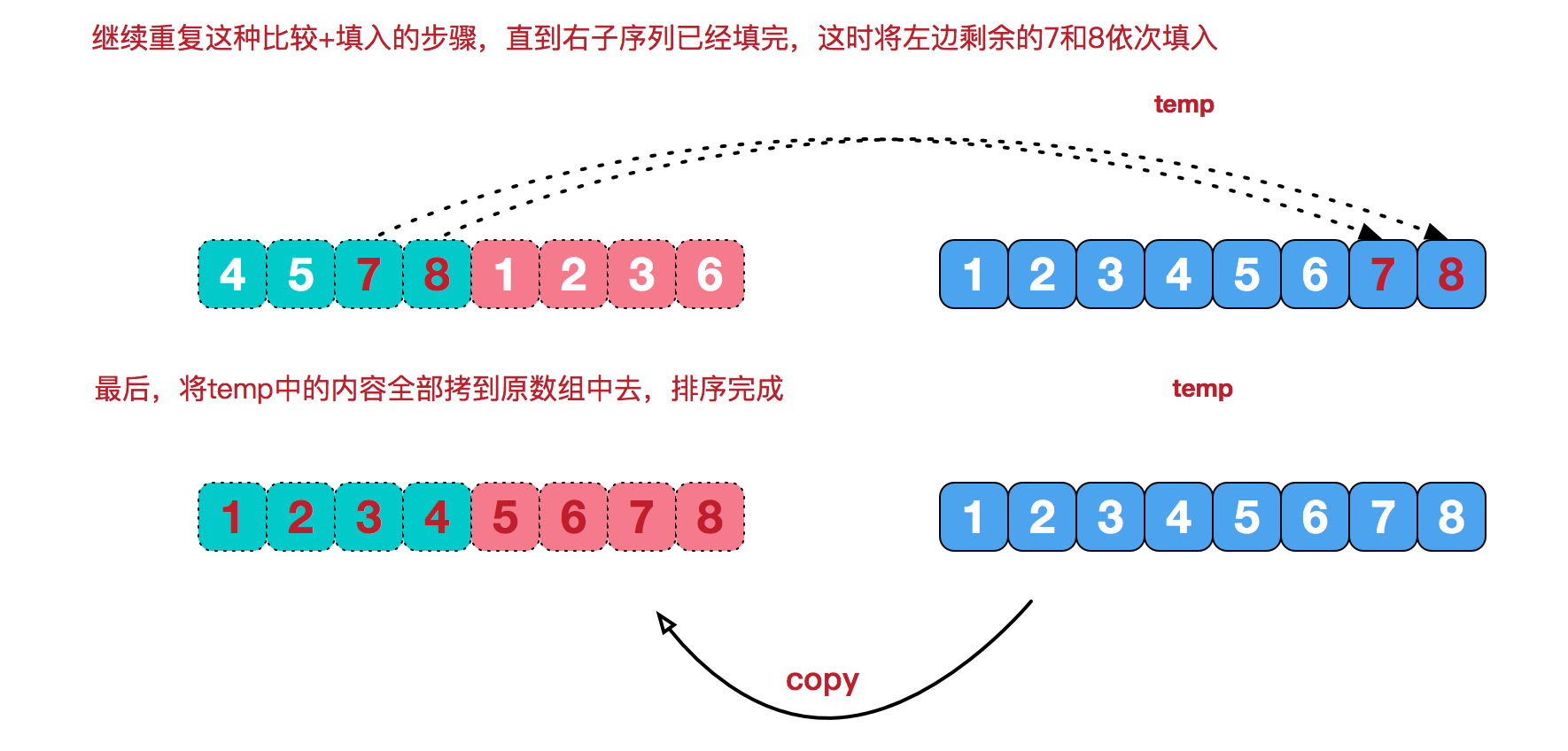
上代码（逆序对）

#include<bits/stdc++.h>
using namespace std;
const int maxn=5e5+10;
int a[maxn],f[maxn];
long long p;
void s(int l,int r)
{
int k,i,m,j;
if(l==r) return;
m=(l+r)/2;
s(l,m);
s(m+1,r);//先分
j=m+1,i=l,k=l;
while(i<=m&&j<=r)
{
if(a[i]>a[j])
{
p+=m-i+1;//统计逆序对
f[k]=a[j];//存入新数组
j++,k++;
}
else {
f[k]=a[i];
i++,k++;
}
}
while(i<=m) {
f[k]=a[i];
i++,k++;
}
while(j<=r)
{
f[k]=a[j];
j++,k++;
}//将剩余元素压入
for(int q=l;q<=r;q++) a[q]=f[q];//修改原数组，保证后续归并的正确性
}
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
s(1,n);
printf("%lld",p);

return 0;
}

然后你就学会啦

二、树状数组

这个要不专门讲吧

我们下一篇博客见AWA

三、三维偏序

cdq分治

离散化+归并排序降维打击+树状数组计数

具体的退役了再完善吧

上代码

 

#include<bits/stdc++.h>
using  namespace std;
const int N=2e5+100;
struct node
{
    int a,b,c,f,w;
}e[N],g[N];
int d[N],n,k,cnt,ans[N];
int lowbit(int x)
{
    return x&(-x); 
}
void add(int x,int y)
{
    while(x<=k)
    {
        d[x]+=y;
        x+=lowbit(x);
    }
}
int find(int x)
{
    int ans=0;
    while(x!=0)
    {
        ans+=d[x];
        x-=lowbit(x);
    }
    return ans;
}
bool cmp(node x,node y)
{
    if(x.a==y.a)
    {
        if(x.b==y.b) return x.c<y.c;
        else return x.b<y.b;
    }
    else return x.a<y.a;
}
void cdq(int l,int r)
{
    int mid=(l+r)/2;
    if(l==r) return;
    cdq(l,mid);
    cdq(mid+1,r);
    int h=l,t=mid+1,tot=l;
    while(h<=mid&&t<=r)
    {
        if(g[h].b<=g[t].b)
        {
            add(g[h].c,g[h].w);
            e[tot++]=g[h++];
        }
        else 
        {
            g[t].f+=find(g[t].c);
            e[tot++]=g[t++];
        }
    }
    while(h<=mid) 
    {
        add(g[h].c,g[h].w);
        e[tot++]=g[h++];
    }
    while(t<=r) 
    {
        g[t].f+=find(g[t].c);
        e[tot++]=g[t++];
    }
    for(int i=l;i<=mid;i++)
    add(g[i].c,-g[i].w);
    for(int i=l;i<=r;i++)
    g[i]=e[i];
}
int main()
{
    cin>>n>>k;
    for(int i=1;i<=n;i++)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        e[i].a=x;
        e[i].b=y;
        e[i].c=z;
    }
    sort(e+1,e+1+n,cmp);
    for(int i=1;i<=n;i++)
    {
        if(e[i].a!=g[cnt].a||e[i].b!=g[cnt].b||e[i].c!=g[cnt].c)    
        {
            g[++cnt]=e[i];
            g[cnt].w=1;
        }
        else g[cnt].w++;
    }
    cdq(1,cnt);
    for(int i=1;i<=cnt;i++)
    {
        if(g[i].w==1) ans[g[i].f]++;
        if(g[i].w>1) ans[g[i].f+g[i].w-1]+=g[i].w;
    }
    for(int i=0;i<n;i++)
    cout<<ans[i]<<endl;
    return  0;
}