拓扑排序

拓扑排序

简介

拓扑排序是将偏序的数据线性化的一种排序方法。复习下偏序和全序的概念：

全序关系是偏序关系的一个子集。

全序是集合内任何一对元素都是可比较的，比如数轴上的点都具有一个线性的数值，因此根据数值就可以进行比较。

偏序是集合内不是所有元素都是可以比较的，比如平面内的点由横坐标和纵坐标组成，是不可直接比较大小的。这是因为横坐标和纵坐标是两个维度，在每个维度内都可以用数值比较，但是维度之间不可量化比较（就像学习成绩和身体素质之间无法量化比较）。当然偏序是个数学概念，未必是多维度引发的不可比较，只需满足以下关系即满足偏序关系：

设 P 是集合，P 上的二元关系“≤”满足以下三个条件，则称“≤”是 P 上的偏序关系（或部分序关系）：

（1）自反性：a≤a，∀a∈P；

（2） 反对称性：∀a，b∈P，若 a≤b 且b≤a，则 a=b；

（3） 传递性：∀a，b，c∈P，若 a≤b 且b≤c，则 a≤c；

注意这里的“≤”是一个自定义的二元运算符，而不是通常的线性运算的大小关系。

理解了偏序关系之后，拓扑排序就是将偏序关系线性化。举一个具体场景，在有向无环图中，“节点 A 是否可由节点 B 到达”即是一种偏序关系。在该有向无环图中节点，在不移动的情况下可以到达自身，因此满足自反性。且在有向无环图中不存在环，若 A 可到达 B 且 B可到达A，则A，B 必是相同节点，因此满足反对称性。当节点 A 可以到达节点 B，且节点 B 可以到达节点C 时，节点 A 也可以到达节点 C，因此满足传递性。

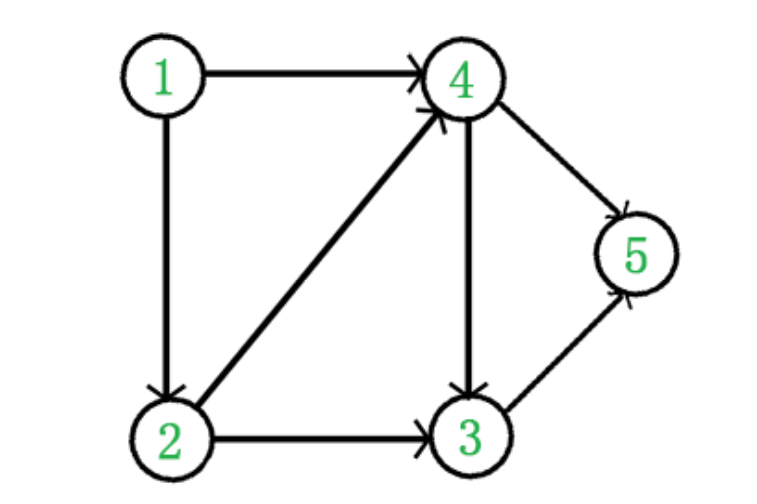
在该场景下，拓扑排序即是将有向无环图中所有节点按照“节点 A 是否可由节点 B 到达”来进行线性化排序。如上图所示，对它进行拓扑排序可以使用深度优先算法完成，深度优先算法可以复习课件，其过程大概如下。

1. 选取顶点 s（一般选取入度比较小的节点更合适，比如上图的节点 1），标记状态
2. 若 s 有未被访问的邻居，则选择邻居标记状态继续访问，否则返回
3. 如果一次深度优先搜索还有节点未被访问，则重复步骤 1，直到所有节点被访问到

这种方法可以将满足偏序关系的有向无环图线性化为🎧一种排序结果：1，2，4，3，5。当然对于更复杂的有向无环图可能有多种合法的排序结果。

实现

实现代码如下：

//
// Created by lenovo on 2022/5/1.
//
#include <utility>

#include "iostream"
#include "vector"
#include "fstream"
using namespace std;

typedef struct EdgeNode
{
    int index;  				//邻接点
    struct EdgeNode *next;      //链表，指向下一个邻接点
}EdgeNode;

typedef struct PointNode    	//顶点表节点
{
    int in;                 	//顶点入度
    int data;               	//顶点信息
    EdgeNode* firstEdge;    	//边表头指针
    PointNode(){in=NULL;data= NULL;firstEdge= nullptr;}
}PointNode;

typedef struct Graph{
    int NumPoint,NumEdge;
    PointNode* arr;
}Graph;

void read_file(Graph* G){           //构造图Graph
    ifstream inputData;
    string input_file_path="..\\input.txt";		//示例输入在同级目录input.txt
    inputData.open(input_file_path, ios::in);
    string line;
    int tmp=0;
    int i=0;
    EdgeNode *e;
    while (inputData>>line){
        int bracketPos = line.find(',');
        int from = stoi(line.substr(0, bracketPos));
        int to= stoi(line.substr(bracketPos+1,line.size()-bracketPos));
        G->NumEdge++;                               //增加边
        if(from!=tmp){tmp=from;G->NumPoint++;}      //增加新的节点

        /*保存边信息*/
        e = (EdgeNode*)malloc(sizeof(EdgeNode));
        e->index = to;

        e->next = G->arr[from].firstEdge;
        G->arr[from].firstEdge = e;
        G->arr[to].in++;
    }
    inputData.close();

}

/*获取输入的边的数量*/
int read_num(){
    ifstream inputData;
    string input_file_path="..\\input.txt";
    inputData.open(input_file_path, ios::in);
    string line;
    int tmp=0;
    while (inputData>>line){
       tmp++;
    }
    inputData.close();
    return tmp;
}

int ToupuSort(Graph* G){

    EdgeNode* edge;
    int next;
    vector<int> stack;
    int count=0;
    for(int i=0;i<G->NumPoint;++i){             //栈stack存储入度为0的节点,需排除0节点
        if(G->arr[i].in==0)
            stack.push_back(i);
    }
    int out;
    while (stack[0]!=stack.back()){                       //当栈为非空
        out=stack.back();
        cout<<out<<",";
        stack.pop_back();
        count++;

        for(edge=G->arr[out].firstEdge;edge;edge=edge->next){           //更新邻接点的入度，-1
            next=edge->index;
            if(!(--G->arr[next].in))       //邻接节点入度原为1，则入栈
                stack.push_back(next);

        }
    }

    if(count<G->NumPoint){              //有环
        return 0;
    }else
        return 1;          //无环，且全部输出

}


int main(){
    Graph G;
    PointNode arry[read_num()];	
    G.arr=arry;				
    read_file(&G);      //构建图
    ToupuSort(&G);      //输出拓扑排序
    return 0;
}

示例输入：

1,2
1,4
2,4
2,3
3,5
4,3
4,5

示例输出:

1，2，4，3，5