HLS Coding Style: Hardware Efficient C Code

Hardware Efficient C Code

When C code is compiled for a CPU, the complier transforms and optimizes the C code into
a set of CPU machine instructions. In many cases, the developers work is done at this stage.
If however, there is a need for performance the developer will seek to perform some or all
of the following:
• Understand if any additional optimizations can be performed by the compiler.
• Seek to better understand the processor architecture and modify the code to take
advantage of any architecture specific behaviors (for example, reducing conditional
branching to improve instruction pipelining)
• Modify the C code to use CPU-specific intrinsics to perform key operations in parallel.
(for example, ARM NEON intrinsics)

The same methodology applies to code written for a DSP or a GPU, and when using an
FPGA: an FPGA device is simply another target.
C code synthesized by Vivado HLS will execute on an FPGA and provide the same
functionality as the C simulation. In some cases, the developers work is done at this stage.

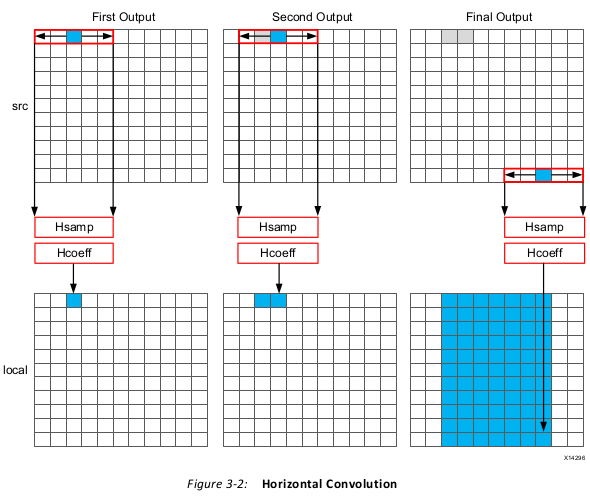
Typical C Code for a Convolution Function

The algorithm structure can be summarized as follows:

 1 template<typename T, int K>
 2 static void convolution_orig(
 3 int width,
 4 int height,
 5 const T *src,
 6 T *dst,
 7 const T *hcoeff,
 8 const T *vcoeff) {
 9 T local[MAX_IMG_ROWS*MAX_IMG_COLS];
10 // Horizontal convolution
11 HconvH:for(int col = 0; col < height; col++){
12 HconvWfor(int row = border_width; row < width - border_width; row++){
13 Hconv:for(int i = - border_width; i <= border_width; i++){
14 }
15 }
16 // Vertical convolution
17 VconvH:for(int col = border_width; col < height - border_width; col++){
18 VconvW:for(int row = 0; row < width; row++){
19 Vconv:for(int i = - border_width; i <= border_width; i++){
20 }
21 }
22 // Border pixels
23 Top_Border:for(int col = 0; col < border_width; col++){
24 }
25 Side_Border:for(int col = border_width; col < height - border_width; col++){
26 }
27 Bottom_Border:for(int col = height - border_width; col < height; col++){
28 }
29 }

 

 

const int conv_size = K;
const int border_width = int(conv_size / 2);
#ifndef __SYNTHESIS__
T * const local = new T[MAX_IMG_ROWS*MAX_IMG_COLS];
#else // Static storage allocation for HLS, dynamic otherwise
T local[MAX_IMG_ROWS*MAX_IMG_COLS];
#endif
Clear_Local:for(int i = 0; i < height * width; i++){
local[i]=0;
}
// Horizontal convolution
HconvH:for(int col = 0; col < height; col++){
HconvWfor(int row = border_width; row < width - border_width; row++){
int pixel = col * width + row;
Hconv:for(int i = - border_width; i <= border_width; i++){
local[pixel] += src[pixel + i] * hcoeff[i + border_width];
}
}
}

The first issue for the quality of the FPGA implementation is the array local. Since this is
an array it will be implemented using internal FPGA block RAM. This is a very large memory
to implement inside the FPGA. It may require a larger and more costly FPGA device. The use
of block RAM can be minimized by using the DATAFLOW optimization and streaming the
data through small efficient FIFOs, but this will require the data to be used in a streaming
manner.

The next issue is the initialization for array local. The loop Clear_Local is used to set
the values in array local to zero. Even if this loop is pipelined, this operation will require
approximately 2 million clock cycles (HEIGHT*WIDTH) to implement. This same initialization
of the data could be performed using a temporary variable inside loop HConv to initialize
the accumulation before the write.

Finally, the throughput of the data is limited by the data access pattern.
• For the first output, the first K values are read from the input.
• To calculate the second output, the same K-1 values are re-read through the data input
port.
• This process of re-reading the data is repeated for the entire image.

Clear_Dst:for(int i = 0; i < height * width; i++){
dst[i]=0;
}
// Vertical convolution
VconvH:for(int col = border_width; col < height - border_width; col++){
VconvW:for(int row = 0; row < width; row++){
int pixel = col * width + row;
Vconv:for(int i = - border_width; i <= border_width; i++){
int offset = i * width;
dst[pixel] += local[pixel + offset] * vcoeff[i + border_width];
}
}
}

This code highlights similar issues to those already discussed with the horizontal
convolution code.
• Many clock cycles are spent to set the values in the output image dst to zero. In this
case, approximately another 2 million cycles for a 1920*1080 image size.
• There are multiple accesses per pixel to re-read data stored in array local.
• There are multiple writes per pixel to the output array/port dst.

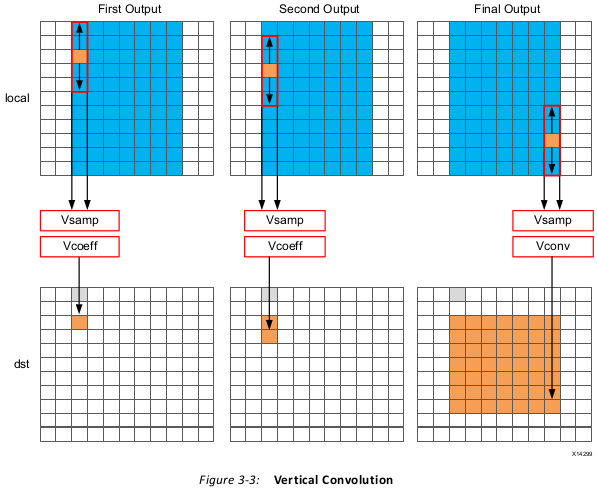
Another issue with the code above is the access pattern into array local. The algorithm
requires the data on row K to be available to perform the first calculation. Processing data
down the rows before proceeding to the next column requires the entire image to be stored
locally. In addition, because the data is not streamed out of array local, a FIFO cannot be
used to implement the memory channels created by DATAFLOW optimization. If DATAFLOW
optimization is used on this design, this memory channel requires a ping-pong buffer: this
doubles the memory requirements for the implementation to approximately 4 million data
samples all stored locally on the FPGA.

int border_width_offset = border_width * width;
int border_height_offset = (height - border_width - 1) * width;
// Border pixels
Top_Border:for(int col = 0; col < border_width; col++){
int offset = col * width;
for(int row = 0; row < border_width; row++){
int pixel = offset + row;
dst[pixel] = dst[border_width_offset + border_width];
}
for(int row = border_width; row < width - border_width; row++){
int pixel = offset + row;
dst[pixel] = dst[border_width_offset + row];
}
for(int row = width - border_width; row < width; row++){
int pixel = offset + row;
dst[pixel] = dst[border_width_offset + width - border_width - 1];
}
}
Side_Border:for(int col = border_width; col < height - border_width; col++){
int offset = col * width;
for(int row = 0; row < border_width; row++){
int pixel = offset + row;
dst[pixel] = dst[offset + border_width];
}
for(int row = width - border_width; row < width; row++){
int pixel = offset + row;
dst[pixel] = dst[offset + width - border_width - 1];
}
}
Bottom_Border:for(int col = height - border_width; col < height; col++){
int offset = col * width;
for(int row = 0; row < border_width; row++){
int pixel = offset + row;
dst[pixel] = dst[border_height_offset + border_width];
}
for(int row = border_width; row < width - border_width; row++){
int pixel = offset + row;
dst[pixel] = dst[border_height_offset + row];
}
for(int row = width - border_width; row < width; row++){
int pixel = offset + row;
dst[pixel] = dst[border_height_offset + width - border_width - 1];
}
}

The code suffers from the same repeated access for data. The data stored outside the FPGA
in array dst must now be available to be read as input data re-read multiple time. Even in
the first loop, dst[border_width_offset + border_width] is read multiple times but the
values of border_width_offset and border_width do not change.

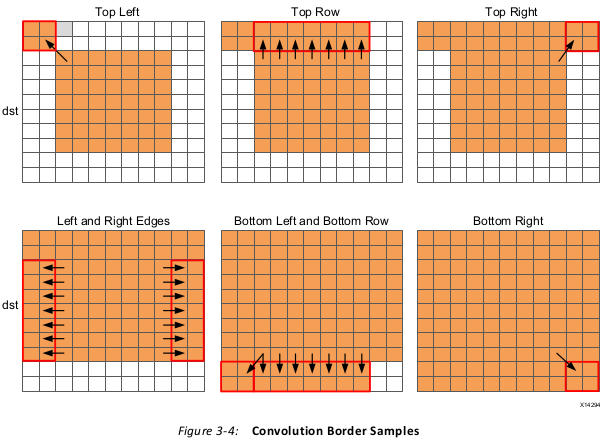
The final aspect where this coding style negatively impact the performance and quality of
the FPGA implementation is the structure of how the different conditions is address. A
for-loop processes the operations for each condition: top-left, top-row, etc. The
optimization choice here is to:
Pipelining the top-level loops, (Top_Border, Side_Border, Bottom_Border) is not
possible in this case because some of the sub-loops have variable bounds (based on the
value of input width). In this case you must pipeline the sub-loops and execute each set of
pipelined loops serially.

The question of whether to pipeline the top-level loop and unroll the sub-loops or pipeline
the sub-loops individually is determined by the loop limits and how many resources are
available on the FPGA device. If the top-level loop limit is small, unroll the loops to replicate
the hardware and meet performance. If the top-level loop limit is large, pipeline the lower
level loops and lose some performance by executing them sequentially in a loop
(Top_Border, Side_Border, Bottom_Border).

 

As shown in this review of a standard convolution algorithm, the following coding styles
negatively impact the performance and size of the FPGA implementation:
• Setting default values in arrays costs clock cycles and performance.
• Multiple accesses to read and then re-read data costs clock cycles and performance.
• Accessing data in an arbitrary or random access manner requires the data to be stored
locally in arrays and costs resources.

 

Ensuring the Continuous Flow of Data and Data Reuse

The ideal behavior is to have the data
samples constantly flow through the FPGA.
• Maximize the flow of data through the system. Refrain from using any coding
techniques or algorithm behavior which limits the flow of data.
• Maximize the reuse of data. Use local caches to ensure there are no requirements to
re-read data and the incoming data can keep flowing.

If the data is transferred from the CPU or system memory to the FPGA it will typically be
transferred in this streaming manner. The data transferred from the FPGA back to the
system should also be performed in this manner.

Using HLS Streams for Streaming Data
One of the first enhancements which can be made to the earlier code is to use the HLS
stream construct, typically referred to as an hls::stream. An hls::stream object can be used to
store data samples in the same manner as an array. The data in an hls::stream can only be
accessed sequentially. In the C code, the hls::stream behaves like a FIFO of infinite depth.

Code written using hls::streams will generally create designs in an FPGA which have
high-performance and use few resources because an hls::stream enforces a coding style
which is ideal for implementation in an FPGA.

Multiple reads of the same data from an hls::stream are impossible. Once the data has been
read from an hls::stream it no longer exists in the stream. This helps remove this coding
practice.

If the data from an hls::stream is required again, it must be cached. This is another good
practice when writing code to be synthesized on an FPGA.

The hls::stream forces the C code to be developed in a manner which ideal for an FPGA
implementation.
When an hls::stream is synthesized it is automatically implemented as a FIFO channel which
is 1 element deep. This is the ideal hardware for connecting pipelined tasks.
There is no requirement to use hls::streams and the same implementation can be performed
using arrays in the C code. The hls::stream construct does help enforce good coding
practices. With an hls::stream construct the outline of the new optimized code is as follows:

template<typename T, int K>
static void convolution_strm(
int width,
int height,
hls::stream<T> &src,
hls::stream<T> &dst,
const T *hcoeff,
const T *vcoeff)
{
hls::stream<T> hconv("hconv");
hls::stream<T> vconv("vconv");
// These assertions let HLS know the upper bounds of loops
assert(height < MAX_IMG_ROWS);
assert(width < MAX_IMG_COLS);
assert(vconv_xlim < MAX_IMG_COLS - (K - 1));
// Horizontal convolution
HConvH:for(int col = 0; col < height; col++) {
HConvW:for(int row = 0; row < width; row++) {
HConv:for(int i = 0; i < K; i++) {
}
}
}
// Vertical convolution
VConvH:for(int col = 0; col < height; col++) {
VConvW:for(int row = 0; row < vconv_xlim; row++) {
VConv:for(int i = 0; i < K; i++) {
}
}
Border:for (int i = 0; i < height; i++) {
for (int j = 0; j < width; j++) {
}
}

 
Some noticeable differences compared to the earlier code are:
• The input and output data is now modelled as hls::streams.
• Instead of a single local array of size HEIGHT*WDITH there are two internal hls::streams
used to save the output of the horizontal and vertical convolutions.

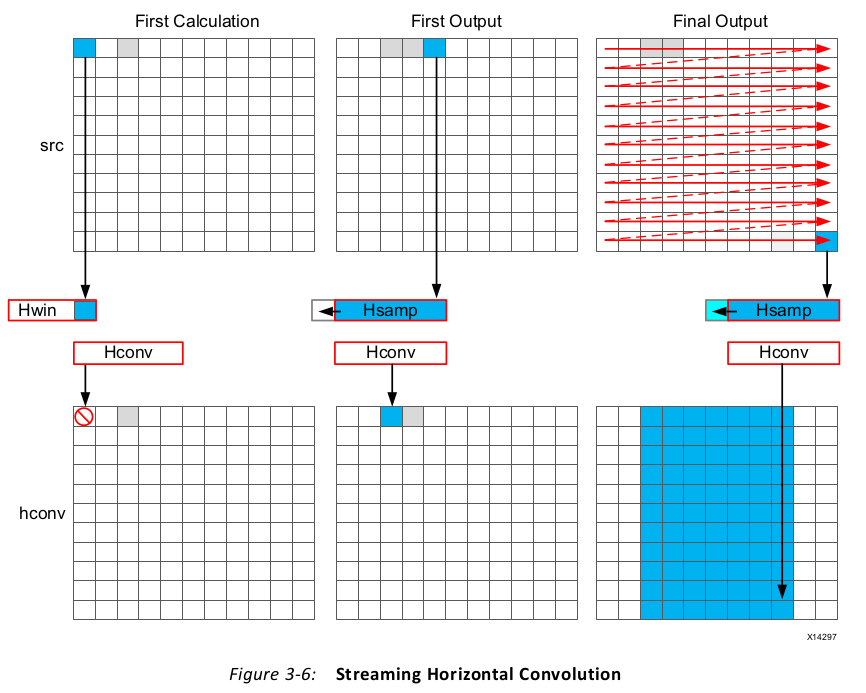
// Horizontal convolution
HConvW:for(int col = 0; col < height; col++) {
HconvW:for(int row = border_width; row < width - border_width; row++){
T in_val = src.read();
T out_val = 0;
HConv:for(int i = 0; i < K; i++) {
hwin[i] = i < K - 1 ? hwin[i + 1] : in_val;
out_val += hwin[i] * hcoeff[i];
}
if (row >= K - 1)
hconv << out_val;
}
}

The algorithm keeps reading input samples a caching them into hwin. Each time is reads a
new sample, it pushes an unneeded sample out of hwin. The first time an output value can
be written is after the Kth input has been read. Now an output value can be written.

Throughout the entire process, the samples in the src input are processed in a
raster-streaming manner. Every sample is read in turn. The outputs from the task are either
discarded or used, but the task keeps constantly computing. This represents a difference
from code written to perform on a CPU.

In a CPU architecture, conditional or branch operations are often avoided. When the
program needs to branch it loses any instructions stored in the CPU fetch pipeline. In an
FPGA architecture, a separate path already exists in the hardware for each conditional
branch and there is no performance penalty associated with branching inside a pipelined
task. It is simply a case of selecting which branch to use.

The outputs are stored in the hls::stream hconv for use by the vertical convolution loop.

 

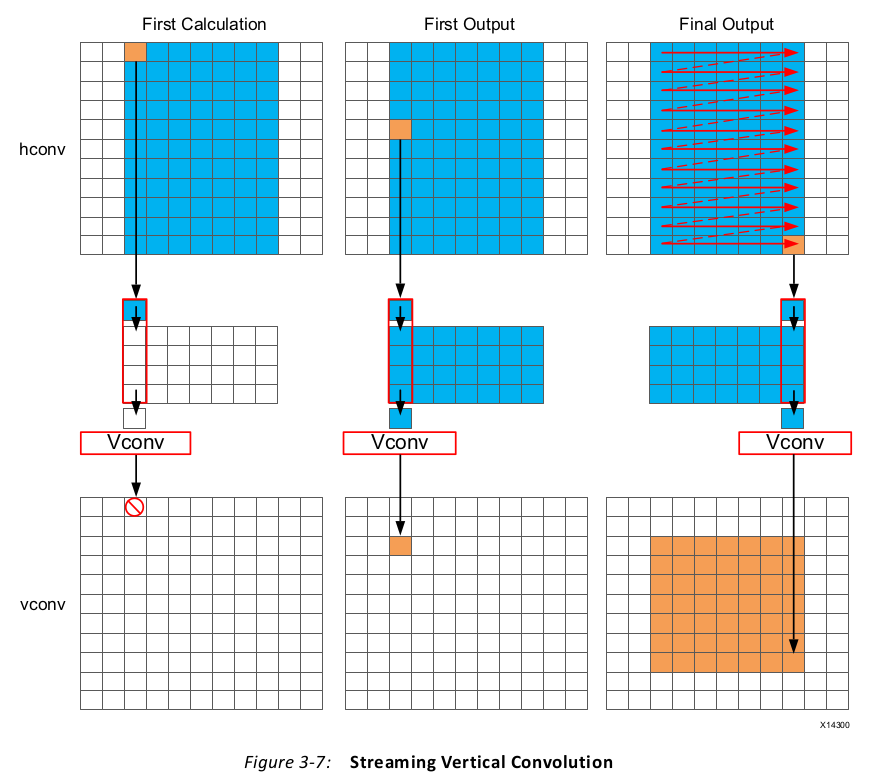
// Vertical convolution
VConvH:for(int col = 0; col < height; col++) {
VConvW:for(int row = 0; row < vconv_xlim; row++) {
#pragma HLS DEPENDENCE variable=linebuf inter false
#pragma HLS PIPELINE
T in_val = hconv.read();
T out_val = 0;
VConv:for(int i = 0; i < K; i++) {
T vwin_val = i < K - 1 ? linebuf[i][row] : in_val;
out_val += vwin_val * vcoeff[i];
if (i > 0)
linebuf[i - 1][row] = vwin_val;
}
if (col >= K - 1)
vconv << out_val;
}
}

A line buffer allows K-1 lines of data to be stored. Each time a new sample is read, another
sample is pushed out the line buffer. An interesting point to note here is that the newest
sample is used in the calculation and then the sample is stored into the line buffer and the
old sample ejected out. This ensure only K-1 lines are required to be cached, rather than K
lines. Although a line buffer does require multiple lines to be stored locally, the convolution
kernel size K is always much less than the 1080 lines in a full video image.

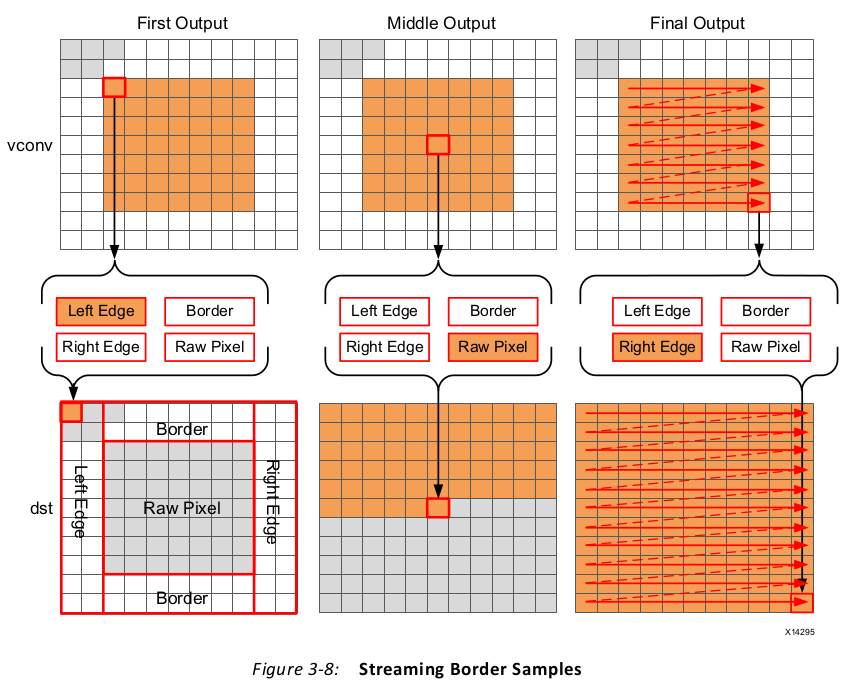
Border:for (int i = 0; i < height; i++) {
for (int j = 0; j < width; j++) {
T pix_in, l_edge_pix, r_edge_pix, pix_out;
#pragma HLS PIPELINE
if (i == 0 || (i > border_width && i < height - border_width)) {
if (j < width - (K - 1)) {
pix_in = vconv.read();
borderbuf[j] = pix_in;
}
if (j == 0) {
l_edge_pix = pix_in;
}
if (j == width - K) {
r_edge_pix = pix_in;
}
}
if (j <= border_width) {
pix_out = l_edge_pix;
} else if (j >= width - border_width - 1) {
pix_out = r_edge_pix;
} else {
pix_out = borderbuf[j - border_width];
}
dst << pix_out;
}
}
}

The final code for this FPGA-friendly algorithm has the following optimization directives
used.

template<typename T, int K>
static void convolution_strm(
int width,
int height,
hls::stream<T> &src,
hls::stream<T> &dst,
const T *hcoeff,
const T *vcoeff)
{
#pragma HLS DATAFLOW
#pragma HLS ARRAY_PARTITION variable=linebuf dim=1 complete
hls::stream<T> hconv("hconv");
hls::stream<T> vconv("vconv");
// These assertions let HLS know the upper bounds of loops
assert(height < MAX_IMG_ROWS);
assert(width < MAX_IMG_COLS);
assert(vconv_xlim < MAX_IMG_COLS - (K - 1));
// Horizontal convolution
HConvH:for(int col = 0; col < height; col++) {
HConvW:for(int row = 0; row < width; row++) {
#pragma HLS PIPELINE
HConv:for(int i = 0; i < K; i++) {
}
}
}
// Vertical convolution
VConvH:for(int col = 0; col < height; col++) {
VConvW:for(int row = 0; row < vconv_xlim; row++) {
#pragma HLS PIPELINE
#pragma HLS DEPENDENCE variable=linebuf inter false
VConv:for(int i = 0; i < K; i++) {
}
}
Border:for (int i = 0; i < height; i++) {
for (int j = 0; j < width; j++) {
#pragma HLS PIPELINE
}
}

Each of the tasks are pipelined at the sample level. The line buffer is full partitioned into
registers to ensure there are no read or write limitations due to insufficient block RAM
ports. The line buffer also requires a dependence directive. All of the tasks execute in a
dataflow region which will ensure the tasks run concurrently. The hls::streams are
automatically implemented as FIFOs with 1 element.

Summary of C for Efficient Hardware

Minimize data input reads. Once data has been read into the block it can easily feed many
parallel paths but the input ports can be bottlenecks to performance. Read data once and
use a local cache if the data must be reused.

Minimize accesses to arrays, especially large arrays. Arrays are implemented in block RAM
which like I/O ports only have a limited number of ports and can be bottlenecks to
performance. Arrays can be partitioned into smaller arrays and even individual registers but
partitioning large arrays will result in many registers being used. Use small localized caches
to hold results such as accumulations and then write the final result to the array.

Seek to perform conditional branching inside pipelined tasks rather than conditionally
execute tasks, even pipelined tasks. Conditionals will be implemented as separate paths in
the pipeline. Allowing the data from one task to flow into with the conditional performed
inside the next task will result in a higher performing system.

Minimize output writes for the same reason as input reads: ports are bottlenecks.
Replicating addition ports simply pushes the issue further out into the system.

For C code which processes data in a streaming manner, consider using hls::streams as
these will enforce good coding practices. It is much more productive to design an algorithm
in C which will result in a high-performance FPGA implementation than debug why the
FPGA is not operating at the performance required.

Sequential I/O Access of Matrix Multiplier

Original Code for the Matrix Multiplier:

#include "matrixmul.h"

void matrixmul(
      mat_a_t a[MAT_A_ROWS][MAT_A_COLS],
      mat_b_t b[MAT_B_ROWS][MAT_B_COLS],
      result_t res[MAT_A_ROWS][MAT_B_COLS])
{
  // Iterate over the rows of the A matrix
   Row: for(int i = 0; i < MAT_A_ROWS; i++) {
      // Iterate over the columns of the B matrix
      Col: for(int j = 0; j < MAT_B_COLS; j++) {
         res[i][j] = 0;
         // Do the inner product of a row of A and col of B
         Product: for(int k = 0; k < MAT_B_ROWS; k++) {
            res[i][j] += a[i][k] * b[k][j];
         }
      }
   }

}

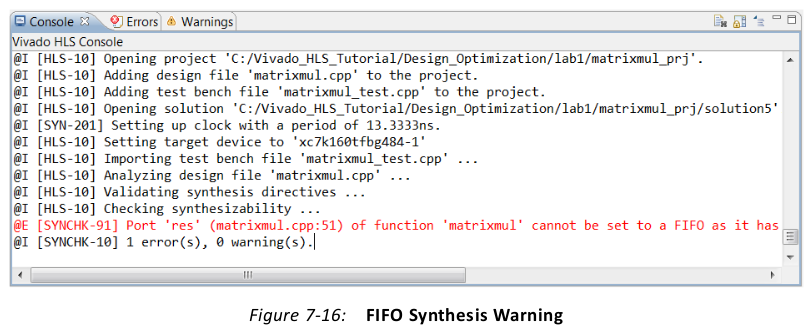
Array res performs writes in the following sequence:

• Write to [0][0] on line57.
• Then a write to [0][0] on line 60.
• Then a write to [0][0] on line 60.
• Then a write to [0][0] on line 60.
• Write to [0][1] on line 57 (after index J increments).
• Then a write to [0][1] on line 60.
• Etc.
Four consecutive writes to address [0][0] does not constitute a streaming access pattern;
this is random access.
There are similar issues reading arrays a and b.

 

Modified Code for the Matrix Multiplier:

#include "matrixmul.h"

void matrixmul(
      mat_a_t a[MAT_A_ROWS][MAT_A_COLS],
      mat_b_t b[MAT_B_ROWS][MAT_B_COLS],
      result_t res[MAT_A_ROWS][MAT_B_COLS])
{
#pragma HLS ARRAY_RESHAPE variable=b complete dim=1
#pragma HLS ARRAY_RESHAPE variable=a complete dim=2
#pragma HLS INTERFACE ap_fifo port=a
#pragma HLS INTERFACE ap_fifo port=b
#pragma HLS INTERFACE ap_fifo port=res
  mat_a_t a_row[MAT_A_ROWS];
  mat_b_t b_copy[MAT_B_ROWS][MAT_B_COLS];
  int tmp = 0;

  // Iterate over the rowa of the A matrix
  Row: for(int i = 0; i < MAT_A_ROWS; i++) {
    // Iterate over the columns of the B matrix
    Col: for(int j = 0; j < MAT_B_COLS; j++) {
#pragma HLS PIPELINE rewind
      // Do the inner product of a row of A and col of B
      tmp=0;
      // Cache each row (so it's only read once per function)
      if (j == 0)
        Cache_Row: for(int k = 0; k < MAT_A_ROWS; k++)
          a_row[k] = a[i][k];

       // Cache all cols (so they are only read once per function)
     if (i == 0)
            Cache_Col: for(int k = 0; k < MAT_B_ROWS; k++)
               b_copy[k][j] = b[k][j];

      Product: for(int k = 0; k < MAT_B_ROWS; k++) {
        tmp += a_row[k] * b_copy[k][j];
      }
      res[i][j] = tmp;
    }
  }
}

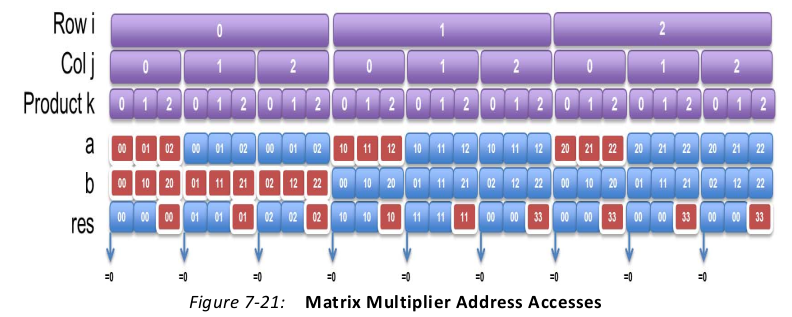
To have a hardware design with sequential streaming accesses, the ports accesses can only
be those shown highlighted in red. For the read ports, the data must be cached internally to
ensure the design does not have to re-read the port. For the write port res, the data must
be saved into a temporary variable and only written to the port in the cycles shown in red.
• In a streaming interface, the values must be accessed in sequential order.
• In the code, the accesses were also port accesses, which High-Level Synthesis is unable
to move around and optimize. The C code specified writing the value zero to port res
at the start of every product loop. This may be part of the intended behavior. HLS
cannot simply decide to change the specification of the algorithm.

Review the code and confirm the following:
• The directives, including the FIFO interfaces, are specified in the code as
pragmas.
• For-loops have been added to cache the row and column reads.
• A temporary variable is used for the accumulation and port res is only written to when
the final result is computed for each value.
• Because the for-loops to cache the row and column would require multiple cycles to
perform the reads, the pipeline directive has been applied to the Col for-loop, ensuring
these cache for-loops are automatically unrolled.

Reference:

1. Xilinx UG902

2.Xilinx UG871