【CF1256】Codeforces Round #598 (Div. 3) 【思维+贪心+DP】
https://codeforces.com/contest/1256

题意:给你a个价值n的物品和b个价值1的物品,问是否存在取物方案使得价值为s
题解:min(s/n,a)*n+b>=s?YES:NO
#include<iostream> #include<cstdio> #include<cstdlib> #include<cmath> #include<algorithm> using namespace std; int a,b,n,s; int main() { int T; scanf("%d",&T); while(T--) { scanf("%d%d%d%d",&a,&b,&n,&s); printf(min(s/n,a)*n+b>=s?"YES\n":"NO\n"); } return 0; }
B:Minimize the Permutation【贪心】


题意:给定一个全排列,你可以选定一个位置i,交换ai和ai+1,每个i只能选一次,问最终最小的排列是什么
题解:从小到大枚举,每次尽可能左移即可
#include<iostream> #include<cstdio> #include<cstdlib> #include<cmath> #include<algorithm> using namespace std; int T,n; int a[101],ad[101],fl[101]; int main() { scanf("%d",&T); while(T--) { scanf("%d",&n); for(int i=1;i<=n;i++){scanf("%d",&a[i]);ad[a[i]]=i;fl[i]=0;} int r=1; for(int i=1;i<=n;i++) { for(int j=ad[i]-1;(!fl[j]) && j>0 && a[j]>a[j+1];j--) { swap(a[j],a[j+1]); swap(ad[a[j]],ad[a[j+1]]); fl[j]=1; } } for(int i=1;i<=n;i++)printf("%d%c",a[i]," \n"[i==n]); } return 0; }
C:Platforms Jumping【贪心】

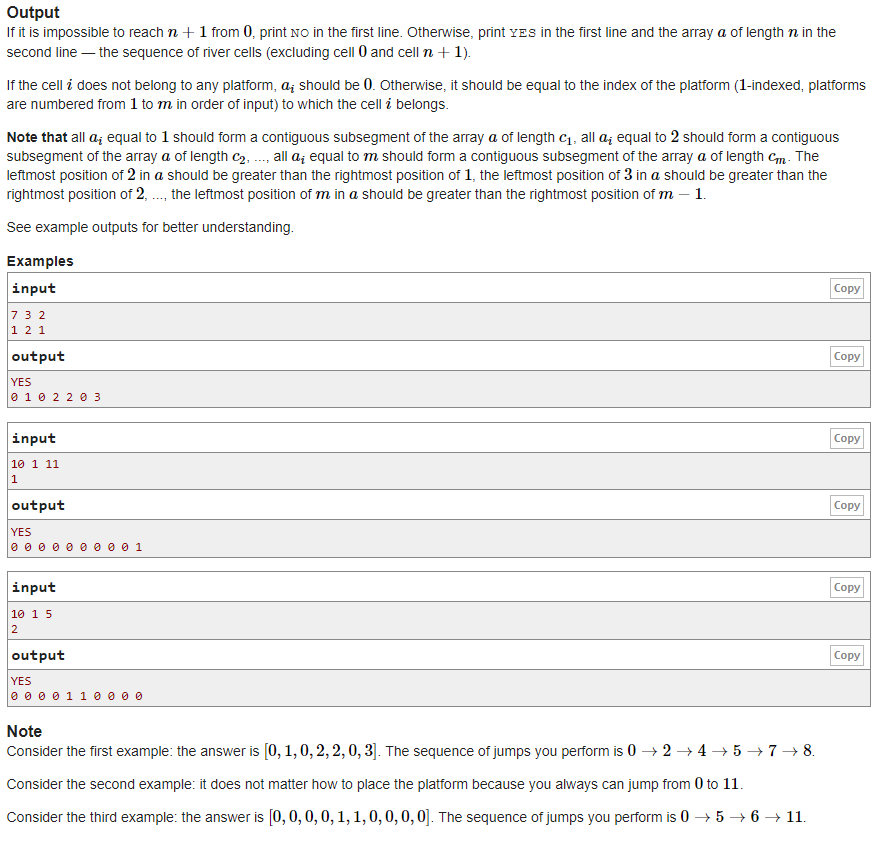
题意:给定一个长度为n的池塘,m块木板以及他们各自的长度,每次你能从i跳到[i+1,i+d],木板之间的相对位置不能移动,求怎么放置木板能使得从0跳到n+1
题解:贪心放到最远端,如果达到当前木板的最右起点限制,则从最右起点限制开始放
#include<iostream> #include<cstdio> #include<cstdlib> #include<cmath> #include<algorithm> #include<cstring> #include<string> #define ll long long using namespace std; int n,m,d; int l[1001],le[1011],ans[1001]; int main() { scanf("%d%d%d",&n,&m,&d); for(int i=1;i<=m;i++)scanf("%d",&l[i]); le[m+1]=n+1; for(int i=m;i>0;i--)le[i]=le[i+1]-l[i]; int now=0; for(int i=1;i<=m;i++) { if(now+d<=le[i]) { for(int j=1;j<=l[i];j++)ans[now+d+j-1]=i; now=now+d+l[i]-1; } else { for(int j=1;j<=l[i];j++)ans[le[i]+j-1]=i; now=le[i]+l[i]-1; } } if(now+d<=n)return !printf("NO\n"); printf("YES\n"); for(int i=1;i<=n;i++)printf("%d%c",ans[i]," \n"[i==n]); return 0; }
D:Binary String Minimizing【贪心】
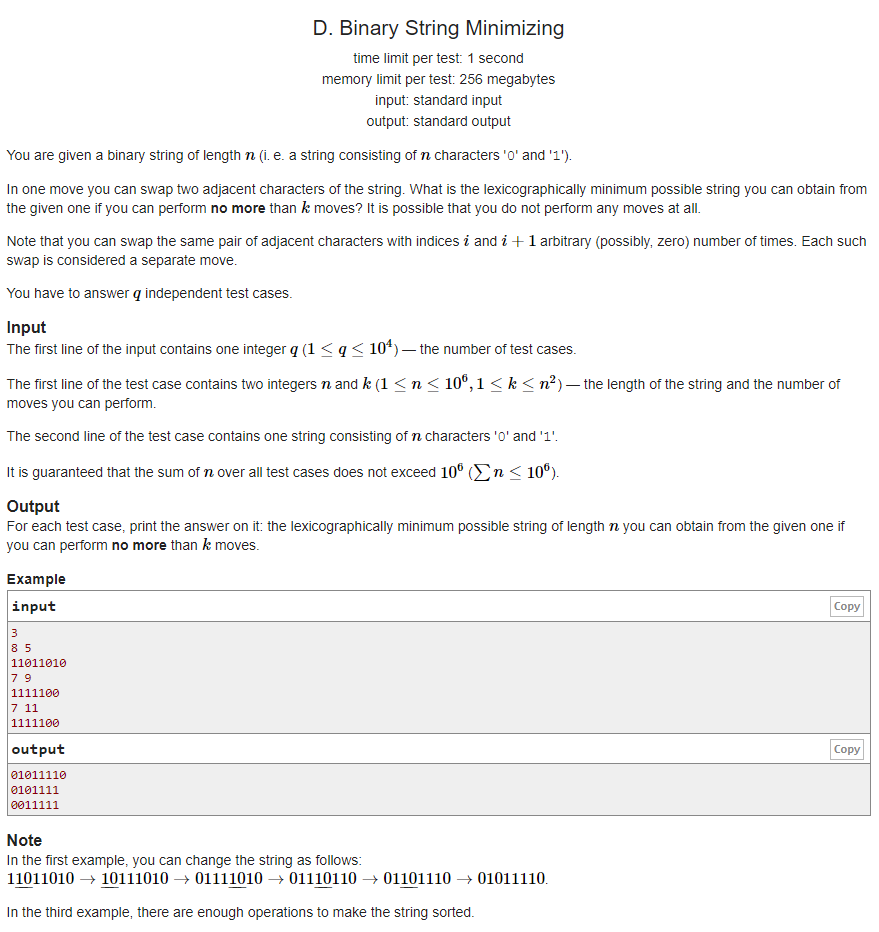
题意:给你一个二进制串,你可以交换ai和ai+1,问交换次数≤k次的最小串
题解:每次贪心将最前面的0移到前面即可
#include<iostream> #include<cstdio> #include<cstdlib> #include<cmath> #include<algorithm> #include<cstring> #include<string> #define ll long long using namespace std; int T,n;ll k; int ad[1000011],adn; char a[1000011]; int main() { scanf("%d",&T); while(T--) { scanf("%d%I64d%s",&n,&k,a); adn=0; for(int i=0;i<n;i++) { if(a[i]=='0') { if(k>=i-adn){swap(a[i],a[adn]);k-=i-adn;adn++;} else {swap(a[i],a[i-k]);break;} } } printf("%s\n",a); } return 0; }
E:Yet Another Division Into Teams【DP】


题意:给定n个数,要求你将数分组,每组数至少有三个,每组的值为这组最大值减去最小值,求怎么分使得所有组的值加起来最小
题解:
先从小到大排序
F[i][1/2/3]表示前i个数,最后一组大小为1/2/3及以上时的最小答案,G[i][1/2/3]表示当前状态的F从哪个前置状态转移过来
最终答案就是F[n][3],然后根据G倒推出分组情况即可
#include<iostream> #include<cstdio> #include<cstdlib> #include<cmath> #include<algorithm> #include<cstring> #include<string> #define ll long long using namespace std; int n; struct node { int v,bh,g; }a[200001]; bool cmp(const node &T1,const node &T2){return T1.v<T2.v;} bool cmp2(const node &T1,const node &T2){return T1.bh<T2.bh;} ll f[200001][4],g[200001][4]; int main() { scanf("%d",&n); for(int i=1;i<=n;i++){scanf("%d",&a[i].v);a[i].bh=i;} sort(a+1,a+1+n,cmp); f[3][3]=a[3].v-a[1].v; g[3][3]=2;g[2][2]=1; for(int i=4;i<=n;i++) { f[i][1]=f[i-1][3];g[i][1]=3; if(i>4)f[i][2]=f[i-1][1]+a[i].v-a[i-1].v,g[i][2]=1; if(i>5) { if(f[i-1][3]<=f[i-1][2])f[i][3]=f[i-1][3]+a[i].v-a[i-1].v,g[i][3]=3; else f[i][3]=f[i-1][2]+a[i].v-a[i-1].v,g[i][3]=2; } else { f[i][3]=f[i-1][3]+a[i].v-a[i-1].v,g[i][3]=3; } } int j=3,t=1; for(int i=n;i>0;i--) { a[i].g=t; if(j==1)t++; j=g[i][j]; } sort(a+1,a+1+n,cmp2); printf("%I64d %d\n",f[n][3],t-1); for(int i=1;i<=n;i++)printf("%d%c",a[i].g," \n"[i==n]); return 0; }
F:Equalizing Two Strings【思维】


题意:给你两个长度相等的串,每次你可以选定一个长度k,在串1中选定起点s1,在串2中选定起点s2,同时翻转两个串ch1[s1,s1+k-1],ch2[s2,s2+k-1],求是否存在翻转方案使得两个字符串最终相等
题解:
首先当两个字符串的字符集不相等时一定为NO
考虑翻转长度为k的字符串,其操作相当于若干次翻转长度为2的字符串,所以我们只考虑翻转长度为2的字符串
根据题意,翻转即为交换i和i+1两个字符
考虑交换i,j两个字符,则需要(j-i)+(j-(i+1))次操作,则一定为奇数
考虑交换i,j,k三个字符,则先交换i到正确位置,再交换j,k,相当于两次交换两个字符的操作,则一定为偶数
对于每一组交换组,若其大小为奇数,那么操作次数一定为偶数,存在方案交换
对于每一组交换组,若其大小为偶数,那么这样的组存在偶数个,则存在方案交换,否则不存在方案交换
特殊的,如果字符串中出现两个及以上相同的字母,那么一定存在方案交换,因为我只需要将两个相同字符换到相邻位置
然后对第二个字符串永远操作交换两个相同字母,那么第二个字符串永远不会变,则此时一定存在方案交换使得字符串1变成字符串2
#include<iostream> #include<cstdio> #include<cstdlib> #include<cmath> #include<algorithm> #include<cstring> #include<string> #define ll long long using namespace std; int T,n; char ch1[200001],ch2[200001]; int cnt1[30],cnt2[30],ffl[30]; int main() { scanf("%d",&T); while(T--) { memset(cnt1,0,sizeof(cnt1)); memset(cnt2,0,sizeof(cnt2)); scanf("%d%s%s",&n,ch1,ch2); for(int i=0;i<n;i++)cnt1[ch1[i]-'a'+1]++,cnt2[ch2[i]-'a'+1]++; int fl=0; for(int i=1;i<=26;i++)if(cnt1[i]!=cnt2[i]){fl=1;break;} if(fl){printf("NO\n");continue;} for(int i=1;i<=26;i++)if(cnt1[i]>1){fl=1;break;} if(fl){printf("YES\n");continue;} int cnt=0; for(int i=0;i<n;i++)cnt2[ch2[i]-'a'+1]=i; memset(ffl,0,sizeof(ffl)); for(int i=0;i<n;i++) { if(ffl[i])continue; ffl[i]=1;int tcnt=1; for(int j=cnt2[ch1[i]-'a'+1];j!=i;j=cnt2[ch1[j]-'a'+1])tcnt++,ffl[j]=1; if(!(tcnt&1))cnt++; } printf(cnt&1?"NO\n":"YES\n"); } return 0; }


