概率与似然

条件概率

在事件B已经发生的条件下，事件A发生的概率，称为事件A在给定B下的条件概率，记作P(A|B)

有A、B、C三个车间生产同一种产品，产量是25%, 35%, 40%，次品率D分别是5%, 4%, 2%。

则：\(P(A) = 0.25, P(D|A) = 0.05\)

条件概率乘法法则

\[P(B|A) = \frac{P(AB)}{P(A)}, P(A|B) = \frac{P(AB)}{P(B)} \]

\[P(AB) = P(A) \cdot P(B|A), P(AB)=P(B) \cdot P(A|B) \]

全概率定理

如果事件A1, A2, ..., An构成一个完备的事件组，并且都有正概率，则对任何一个事件B，有

\[P(B)=\sum_i^n P(A_i) \cdot P(B|A_i) \]

贝叶斯定理

\[P(A_m|B) = \frac{P(A_m)P(B|A_m)}{\sum_i^n P(A_i)P(B|A_i)} \]

其中，

\[\sum_i^n P(A_i)=1, \sum_i^n P(A_i) P(B|A_i) = P(B) \]

而\(A_m\)可以看作一个独立的事件, 所以:

\[P(A|B) = P(A) \times \frac{P(B|A)}{P(B)} \]

其中\(P(A|B)\)叫做后验概率(Posterior probability)，\(P(A)，P(B)\)叫做先验概率（Prior probability），\(\frac{P(B|A)}{P(B)}\)叫做可能性函数或调整因子，\(P(B|A)\)叫做可能性或似然(Likelihood)

\[P(\theta |D) = P(\theta) \times \frac{P(D| \theta)}{P(D)} \]

D - 数据
\(\theta\) - 参数
\(P(\theta | D)\) - 后验
\(P(D|\theta)\) - 似然

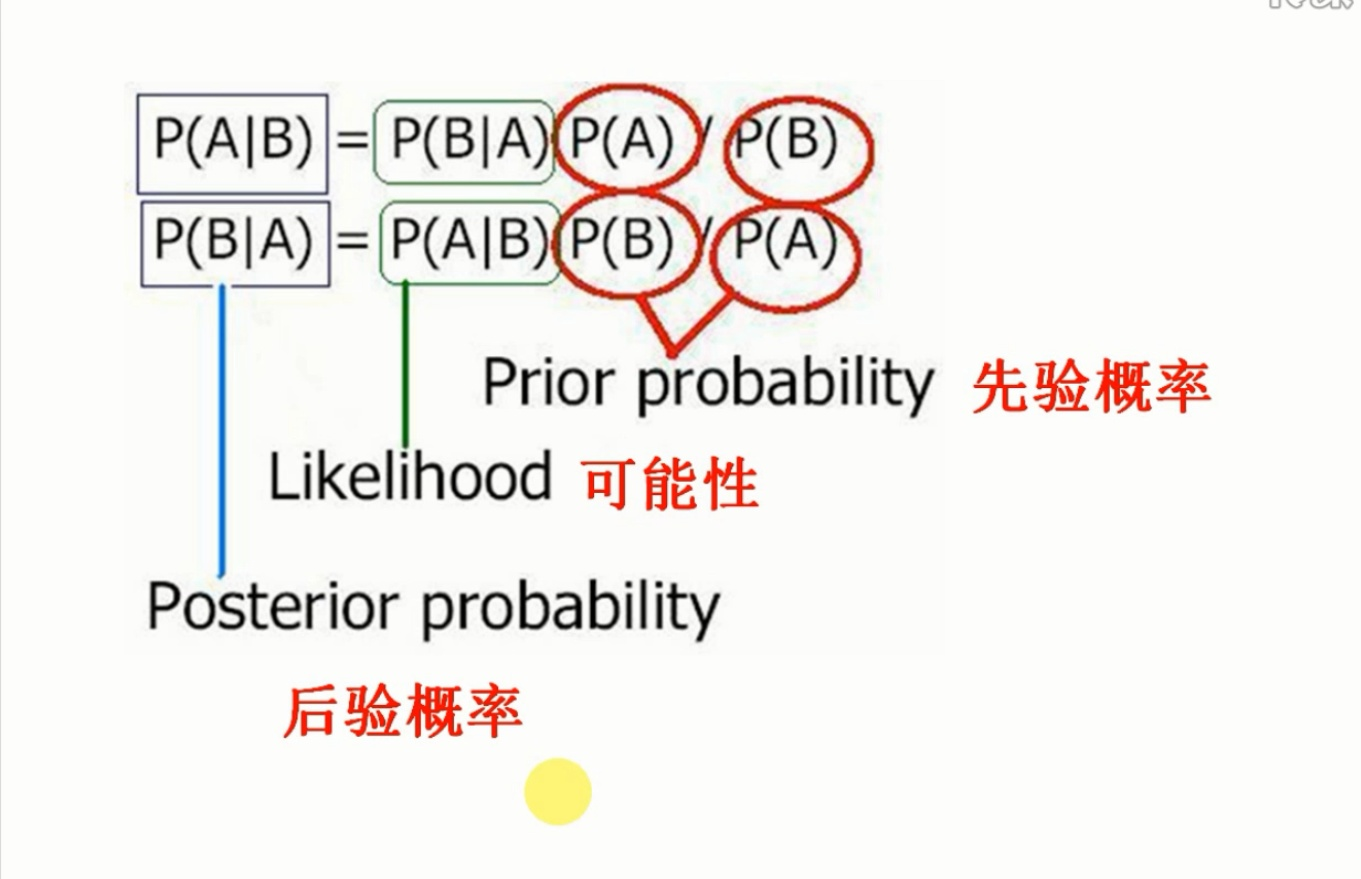
后验概率 = 先验概率 x 调整因子

先验概率：根据以往经验分析得到的概率，通俗就是根据统计和规律得出得概率。
后验概率：就是根据结果推原因，比如知道一个产品是次品求它来自A车间的概率，通过贝叶斯公式可以得到。

似然

根据总总体样本X中抽到的样本\((X_1,...,X_n)\)，对总体分布中的未知参数\(\theta\)（比如正态分布中的均值和方差）进行估计。
最大似然法是要选择一个\(\hat{\theta}\)，使得观察结果出现的可能性最大。对于离散型随机变量，就是估计概率函数中的参数\(\theta\)，对于连续型就是概率密度中的\(\theta\)。

设X为离散型随机变量，有概率函数P(X=x_i)=p(x_i;\theta)，则似然函数L:

\[L(x_1,...,x_n;\theta) = \prod^n_{i=1} p(x_i;\theta) \]

两边取log：

\[\log{L} = \log(\prod^n_{i=1} p(x_i;\theta)) = \sum^n_{i=1} \log{p(x_i;\theta)} ，(或 \sum^n_{i=1} \log{p_\theta (x_i)}) \]

例子

有A、B、C三个车间生产同一种产品，产量是25%, 35%, 40%，次品率是5%, 4%, 2%。
现在从出产产品中检测到一个次品，判断是A车间的出品的概率。

解：

P(A) = 0.25, P(B) = 0.35, P(C)=0.4

次品D:
P(D|A) = 0.05, P(D|B) = 0.04, P(D|C) = 0.02

全厂的次品率：
P(D) = P(D|A)P(A) + P(D|B)P(B) + P(D|C)P(C) = 0.05 x 0.25 + 0.04 x 0.35 + 0.02 x 0.4 = 0.0345

是A车间的出品的概率，根据贝叶斯定理：

\[P(A|D) = \frac{ P(A)P(D|A) }{ P(D) }=\frac{0.25 \times 0.05}{0.0345}=0.362 \]

先验概率：根据以往的经验、统计规律得到的概率，”由因求果“中的因
后验概率：根据结果推原因（给定数据求参数的概率），”由果寻因“中的因
似 然：给定参数求数据的概率

最大似然估计

有一天，有个病人到医院看病。他告诉医生说自己头痛，然后医生根据自己的经验判断出他是感冒了，然后给他开了些药回去吃。
其实医生的大脑是这么工作的，

P(感冒|头痛) = 85%
P(中风|头痛) = 10%
P(脑溢血|头痛) = 5%

然后这个计算机大脑发现，P(感冒|头痛)是最大的，因此就认为呢，病人是感冒了。看到了吗？这个就叫最大似然估计（Maximum likelihood estimation，MLE）。

P(感冒|头痛)，P(中风|头痛)，P(脑溢血|头痛)是先验概率还是后验概率呢？没错，就是后验概率。看到了吧，后验概率可以用来看病.

后验概率起了这样一个用途，根据一些发生的事实（通常是坏的结果），分析结果产生的最可能的原因，然后才能有针对性地去解决问题。

假设f是一个概率密度函数：

\[x -> f(x|\theta) \]

是一个条件概率密度函数（\(\theta\)是给定的）

反过来：

\[\theta -> f(x|\theta) \]

叫做似然函数（x是给定的）

一般把似然函数写成：

\[L(\theta | x) = f(x|\theta) \]

\(\theta\)是因变量。
最大似然估计就是求在\(\theta\)的定义域中，当似然函数取得最大值时\(\theta\)的大小。即，当后验概率最大时 \(\theta\)的大小，也就是说要求最有可能的原因。
由于对数函数不会改变大小关系，所以有时候将似然函数求对数，计算方便。

例子：

我们假设有三种硬币，他们扔到正面的概率分别是1/3，1/2，2/3。我们手上有一个硬币，但是我们并不知道这是哪一种。因此我们做了一下实验，我们扔了80次，有49次正面，31次背面。那么这个硬币最可能是哪种呢？我们动手来算一下。这里θ的定义域是{1/3，1/2，2/3}

\[P(H=49 | p=1/3) = \begin{pmatrix} 80 \\ 49\end{pmatrix} (1/3)^49(1-1/3)^31 = 0.000 \]