[计算几何]POJ 1375 点对圆的切线+线段重叠

http://acm.pku.edu.cn/JudgeOnline/problem?id=1375

 

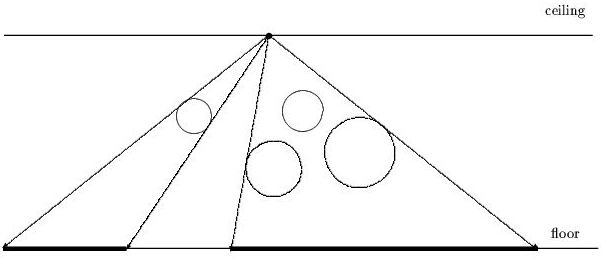
题目大意如上图，ceiling上面有个光源，ceiling和floor有一些圆形的管子，要求出最后floor上光源找不到的区域。

比较简单，直接对每个圆求出两条切线，进而求出被这个圆遮挡住的区域(bx,ex)

最后把这些区域按bx排序，然后线性扫描一遍就可以得到不相交的区域了。

PS:这题精度比较重要，另外求点对圆的切线时先求出点和圆心的向量，然后把这个向量顺时针逆时针各旋转一个角度就可以得到切点的坐标了。

 

#include <stdio.h>
#include <math.h>
#include <algorithm>
using namespace std;
#define eps 1.0e-6
#define equ(x,y) (fabs(x-y)<eps)

struct Point {
    double x,y;
};

struct tnode {
    double bx,ex;
};
inline bool operator<(const tnode &t1,const tnode& t2) {
    return t1.bx<t2.bx||(equ(t1.bx,t2.bx)&&t1.ex<t2.ex);
}

tnode ans[500];

inline void swap(double &x,double &y) {
    double t=x;
    x=y;
    y=t;
}

//将向量p逆时针旋转angle角度
Point Rotate(Point p,double angle) {
    Point res;
    res.x=p.x*cos(angle)-p.y*sin(angle);
    res.y=p.x*sin(angle)+p.y*cos(angle);
    return res;
}

//求Poi对圆(o,r)的两个切点result1和result2
void TangentPoint_PC(Point poi,Point o,double r,Point &result1,Point &result2) {
    double line=sqrt((poi.x-o.x)*(poi.x-o.x)+(poi.y-o.y)*(poi.y-o.y));
    double angle=acos(r/line);
    Point unitvector,lin;
    lin.x=poi.x-o.x;
    lin.y=poi.y-o.y;
    unitvector.x=lin.x/sqrt(lin.x*lin.x+lin.y*lin.y)*r;
    unitvector.y=lin.y/sqrt(lin.x*lin.x+lin.y*lin.y)*r;
    result1=Rotate(unitvector,-angle);
    result2=Rotate(unitvector,angle);
    result1.x+=o.x;
    result1.y+=o.y;
    result2.x+=o.x;
    result2.y+=o.y;
    return;
}

int main() {
    Point bp;
    Point op;
    double r;
    int n;
    while(scanf("%d",&n)!=EOF) {
        if(n==0) continue;
        scanf("%lf %lf",&bp.x,&bp.y);
        for(int i=0;i<n;i++) {
            scanf("%lf %lf %lf",&op.x,&op.y,&r);
            Point r1,r2;
            TangentPoint_PC(bp,op,r,r1,r2);
            double x1=(r1.y*bp.x-r1.x*bp.y)/(r1.y-bp.y);
            double x2=(r2.y*bp.x-r2.x*bp.y)/(r2.y-bp.y);
            if(x1>x2) swap(x1,x2);
            ans[i].bx=x1;
            ans[i].ex=x2;
        }
        sort(ans,ans+n);
        printf("%.2lf",ans[0].bx);
        double prevy=ans[0].ex;
        for(int i=1;i<n;i++) {
            if(!equ(prevy,ans[i].bx)&&ans[i].bx>prevy) {
                printf(" %.2lf\n%.2lf",prevy,ans[i].bx);
            }
            if(prevy<ans[i].ex) prevy=ans[i].ex;
        }
        printf(" %.2lf\n",prevy);
        putchar('\n');
    }

    return 0;
}