HashMap源码分析
基本信息
常量信息
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
特殊说明:MIN_TREEIFY_CAPACITY只有当整个存储的长度大于等于该值(64)后,才会进行链表与红黑树的转换,如果小于该值,则会进行扩容,而非将链表转换为红黑树
基本存储结构
整体存储是通过哈希表(Node<K,V>[] table)将数据存储,在单个槽位中,通过链表+红黑树的方式进行数据存储。
链表数据通过Node存储,结构如下:
| hash | key对应的Hash值 |
| key | key的真实值 |
| value | value的真实值 |
| next | 链表中下一个数据 |
红黑树的节点TreeNode,结构如下:
| parent | 父节点 |
| left | 左孩子 |
| right | 右孩子 |
| prev | 前置节点 |
| red | 是否是红节点 |
简图
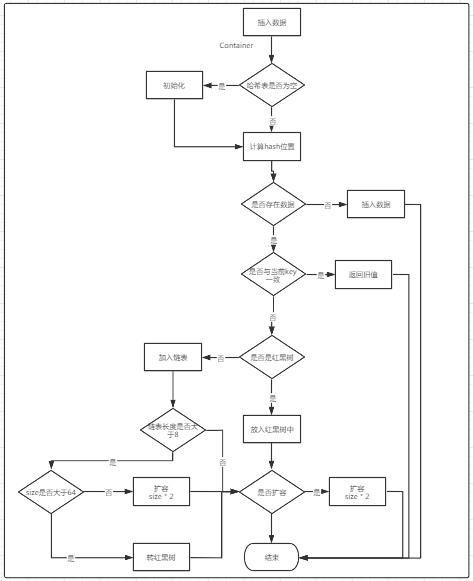
方法分析
tableSizeFor方法
主要计算哈希表的长度,在初始化hashMap时,可以指定初始化长度,但具体初始化长度值由该方法决定。
static final int tableSizeFor(int cap) { int n = cap - 1; n |= n >>> 1; n |= n >>> 2; n |= n >>> 4; n |= n >>> 8; n |= n >>> 16; return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1; }
如,指定长度为13,则计算过程如下:
- 首先,计算n为12。(这里个人认为是为了防止对于正好是2的N次方的数据造成长度计算的错误)
- 进行以下计算
n |= n >>> 1
1 1 0 0
1 1 0
---------
1 1 1 0
n |= n >>> 2
1 1 1 0
1 1
---------
1 1 1 1
后边两步没必要算了,因为都是高位补齐0,没有计算的意义了。
3. 最后就是获取当前实际长度,如果没有超过最大长度,则即为(n+1)了。
resize()方法
主要是在哈希表的容量不够时,即(tab.length > capacity * loadfactofinal Node<K,V>[] resize() Node<K,V>[] oldTab = table; int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold; int newCap, newThr = 0; // 中间省略了部分计算容量的代码逻辑,个人认为比较简单,就不贴这块代码了 threshold = newThr; @SuppressWarnings({"rawtypes","unchecked"}) Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap]; table = newTab; if (oldTab != null) { for (int j = 0; j < oldCap; ++j) { Node<K,V> e; if ((e = oldTab[j]) != null) { oldTab[j] = null; if (e.next == null) // 当前位置只有一个元素,则直接将其放置扩容后的哈希表中 newTab[e.hash & (newCap - 1)] = e; else if (e instanceof TreeNode) // 如果改位置的元素是红黑树,则进入split方法,对红黑树上的每个节点数据进行计算 ((TreeNode<K,V>)e).split(this, newTab, j, oldCap); else { // preserve order // 这里是对链表进行操作,即长度小于8 Node<K,V> loHead = null, loTail = null; // 用于存储在扩容后,数据在低位的数据 Node<K,V> hiHead = null, hiTail = null; // 用于存储在扩容后,数据在高危的数据 Node<K,V> next; do { next = e.next; if ((e.hash & oldCap) == 0) { // 如果元素的hash值(xxx0 xxxx)与原来的哈希表长度相与为0,则表示其高位并没有1,在扩容后位置不用变更 if (loTail == null) loHead = e; else loTail.next = e; // 这里使用的是后插法,避免了在JDK1.7中前插法可能会出现的死循环问题 loTail = e; } else { // 如果非0,则表明其hash值是大于原来哈希表的长度的且在高一位(xxxx1 xxxx)的位置为1,在扩容后的位置会在整个哈希表的高危 if (hiTail == null) hiHead = e; else hiTail.next = e; hiTail = e; } } while ((e = next) != null); if (loTail != null) { loTail.next = null; newTab[j] = loHead; } if (hiTail != null) { hiTail.next = null; newTab[j + oldCap] = hiHead; // 因为扩容后,容量翻倍,这里高危与地位的差距,即原来的哈希表的长度。 } } } } } return newTab; }
特殊说明:计算高低的方式举例说明一下,如hash表的长度为16,在位置7的数据hash值可能为7、23,39。当进行扩容后,容量变为了32,则7、39仍然在原来7的位置,但是23实际是要移到23的位置了
hash(Object key)方法
主要是获取数据的hash值,从代码中可以看到key为null时,直接返回0,也就是在HashMap中是允许key为null的且将其存储在位置0。对于非null的,则是将hash的高16与低16位进行亦或得到结果。这个方法在网上也找了一些说明,个人觉得知乎胖君说的很好,这叫做“扰动函数”,主要是为了混合原始哈希码的高位和低位,以此来加大低位的随机性。
static final int hash(Object key) { int h; return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16); }
putVal(int hash, K key, V value, boolean onlyIfAbsent,boolean evict)方法
主要是将对应的key和value存储在hash表中。
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) { Node<K,V>[] tab; Node<K,V> p; int n, i; if ((tab = table) == null || (n = tab.length) == 0) // 如果当前哈希表没有初始化,则对其进行初始化 n = (tab = resize()).length; if ((p = tab[i = (n - 1) & hash]) == null) // 如果当前下标下没有值,则直接将对应的key存储在改位置 tab[i] = newNode(hash, key, value, null); else { Node<K,V> e; K k; if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) // 如果key与当前的key的hash值和value均一致,则记录当前Node信息 e = p; else if (p instanceof TreeNode) // 当前节点是红黑树,则进入红黑树插入数据的方法 e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value); else { // 链表插入 for (int binCount = 0; ; ++binCount) { if ((e = p.next) == null) { // 如果链表的下一个位置为null, 则直接将该值写入在下一个位置 p.next = newNode(hash, key, value, null); if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st // 这里判断是否超过8,如果超过需要将链表转为红黑树 treeifyBin(tab, hash); break; } if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) //当前节点的key与要插入的key的hash值与key值均一致,则结束查找 break; p = e; } } if (e != null) { // existing mapping for key V oldValue = e.value; if (!onlyIfAbsent || oldValue == null) // 如果允许替换新值或者原值为null, 则写入新的value值 e.value = value; afterNodeAccess(e); return oldValue; } } ++modCount; // 记录修改次数,这是是为了fast-fail(快速失败)机制 if (++size > threshold) // 超过阈值,则进行扩容,也就是说是先写入后扩容 resize(); afterNodeInsertion(evict); // 貌似没有啥意义 return null; }
getNode(int hash, Object key)方法
主要提供根据key查询value的方法,我们经常使用containsKey方法其实底层和get方法使用均是该方法实现的,所以效率是一样的
final Node<K,V> getNode(int hash, Object key) { Node<K,V>[] tab; Node<K,V> first, e; int n; K k; if ((tab = table) != null && (n = tab.length) > 0 && (first = tab[(n - 1) & hash]) != null) { if (first.hash == hash && // always check first node ((k = first.key) == key || (key != null && key.equals(k)))) return first; if ((e = first.next) != null) { if (first instanceof TreeNode) // 进行红黑树查找 return ((TreeNode<K,V>)first).getTreeNode(hash, key); do { // 循环进行链表查找,这里最大的循环次数其实就是7 if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) return e; } while ((e = e.next) != null); } } return null; }


