图的实现、包括bfs,dfs,dijkstra、floyd
package pri.wdw.algorithm.graph;
import java.util.*;
/**
* <p>@author wdw</p>
* <p>@date 2020/5/6 22:08</p>
* <p>@description </p>
*/
public class Graph {
//顶点
protected final List<String> vertexes;
//边
protected final int[][] edges;
/**
* @param vertexes 每个节点的名称
*/
public Graph(String... vertexes) {
int length = vertexes.length;
this.vertexes = new ArrayList<>(length);
edges = new int[length][length];
//自己结点设为 0 ,不可到达结点设为 -1
for (int i = 0; i < edges.length; i++) {
Arrays.fill(edges[i], -1);
edges[i][i] = 0;
}
this.vertexes.addAll(Arrays.asList(vertexes));
}
/**
* 无向图
*
* @param v1 在邻接矩阵的横坐标
* @param v2 临界矩阵纵坐标
* @param weight 权值
* @return 插入是否成功
*/
public boolean addEdge(int v1, int v2, int weight) {
if (v1 < 0 || v1 >= edges.length || v2 < 0 || v2 >= edges.length || weight <= 0) {
return false;
} else {
this.edges[v1][v2] = weight;
this.edges[v2][v1] = weight;
return true;
}
}
/**
* @return
*/
public int[][] getEdge() {
return this.edges;
}
public String getVertex(int index) {
return this.vertexes.get(index);
}
/**
* 添加一个节点
*
* @param vertex 节点
*/
public void addVertexes(String vertex) {
vertexes.add(vertex);
}
/**
* @param v1
* @param v2
* @return 获取权值
*/
public int getWeight(int v1, int v2) {
return this.edges[v1][v2];
}
/**
* @return 获取结点的个数
*/
public int size() {
return vertexes.size();
}
/**
* @return 打印邻接矩阵
*/
@Override
public String toString() {
StringBuilder builder = new StringBuilder();
for (int i = 0; i < edges.length; i++) {
builder.append(vertexes.get(i))
.append(' ')
.append(Arrays.toString(edges[i]))
.append('\n');
}
builder.deleteCharAt(builder.length() - 1);
return builder.toString();
}
/**
* 暴漏给外部的方法
*
* @param index 当前正在被访问的结点
*/
public void dfs(int index) {
int length = this.edges.length;
//鲁棒性
if (index >= length || index < 0) throw new IllegalArgumentException();
this.dfs(index, new boolean[length]);
}
/**
* DFS
* <p>
* 每次都是优先访问 当前节点的邻接节点,并且以这个邻接节点,访问下一个邻接结点。
* <p>
* 1、访问初始节点A,并且标记节点被访问
* 2、访问 A 的下一个邻接结点 B未被访问,并且A-B连通,以B为根递归,否则访问A 的 下一个邻接结点C
* <p>
* 访问顺序 A-B-C-D-E
*
* @param index 当前正在被访问的结点
* @param isVisited 当前结点是否被访问标志
*/
private void dfs(int index, boolean[] isVisited) {
int length = this.edges.length;
//标记已经访问
isVisited[index] = true;
//打印
System.out.println(this.vertexes.get(index));
//每次取模,可以从任意一个结点开始,每次都访问逻辑意义上(循环)的下一个结点,直到i返回和 index 一样
for (int i = (index + 1) % length; i != index; i = (i + 1) % length) {
if (!isVisited[i] && this.edges[index][i] != -1) {
dfs(i, isVisited);
}
}
}
/**
* BFS最大广度遍历,和二叉树的层序遍历类似
* <p>
* ① 访问顶点vi ;
* <p>
* ② 访问vi 的所有未被访问的邻接点w1 ,w2 , …wk ;
* <p>
* ③ 依次从这些邻接点(在步骤②中访问的顶点)出发,访问它们的所有未被访问的邻接点; 依此类推,直到图中所有访问过的
*/
public void bfs(int index) {
int length = this.edges.length;
//鲁棒性
if (index >= length || index < 0) throw new IllegalArgumentException();
//辅助队列
Queue<Integer> queue = new LinkedList<>();
//记录是否被访问
boolean[] isVisited = new boolean[length];
isVisited[index] = true;
queue.offer(index);
//递归调用顺序为 访问vi 的所有未被访问的邻接点w1 ,w2 , …wk
while (!queue.isEmpty()) {
index = queue.poll();
System.out.println(this.vertexes.get(index));
//依次压入该结点的邻接结点,之后再进行打印。
for (int j = (index + 1) % length; j != index; j = (j + 1) % length) {
if (!isVisited[j] && this.edges[index][j] != -1) {
queue.offer(j);
isVisited[j] = true;
}
}
}
}
/**
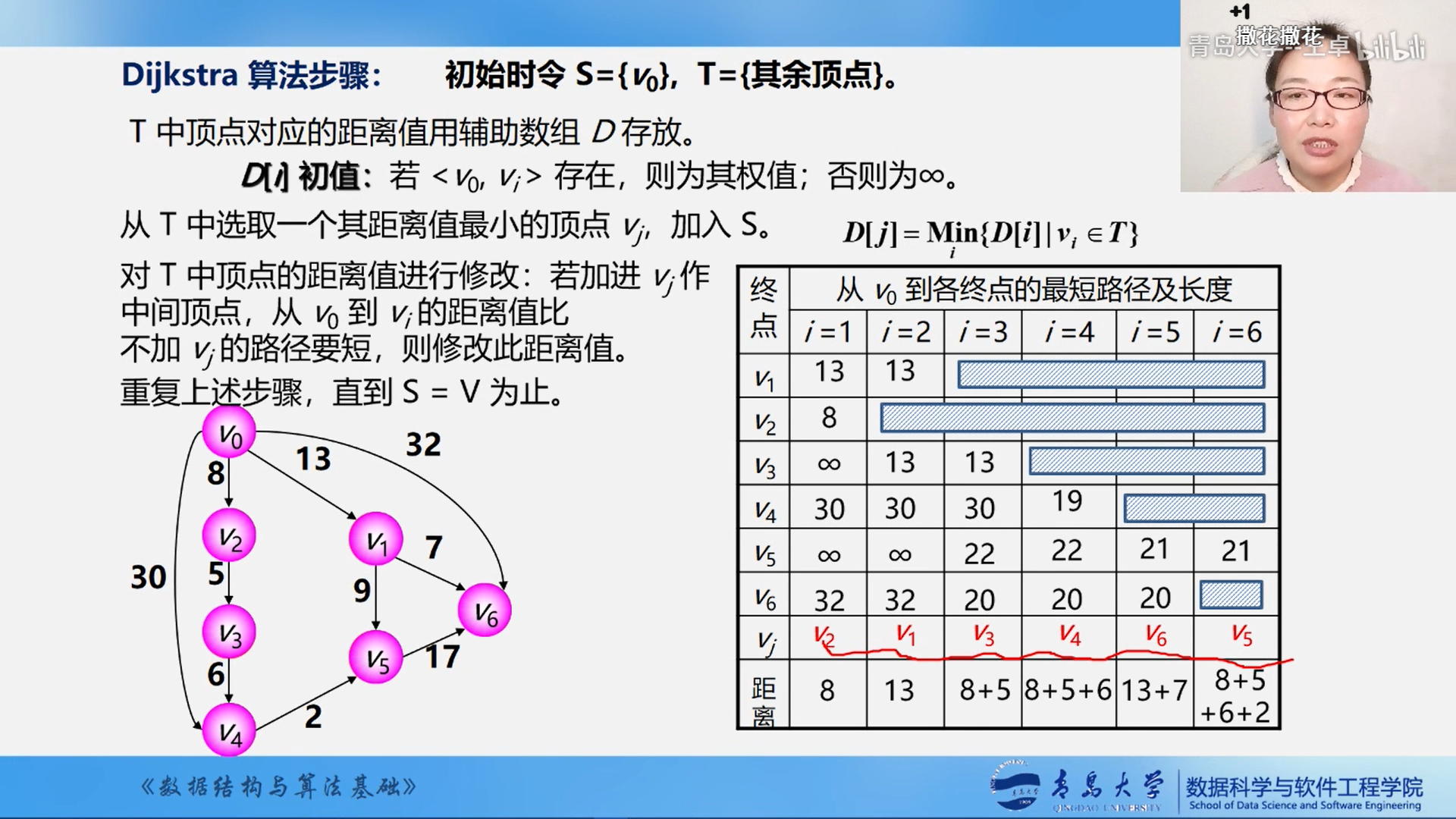
* dijkstra算法应用到了广度优先遍历,本质上是一个贪心算法。
* 可以解决 单元最短路径(一个结点到所有结点之间的最短距离)。
*
* @param index 该结点在邻接矩阵的位置
* @return 该结点到每个结点的最短路径
*/
public int[] dijkstra(int index) {
int length = this.size();
//0、初始化两个容器,未计算的结点、计算的距离。
int[] distances = this.edges[index].clone();
HashSet<Integer> notCalculatedVertexes = new HashSet<>(length - 1);
for (int i = 0; i < this.size(); i++) {
if (i != index) notCalculatedVertexes.add(i);
}
//1、初始化的minIndex,就是需要求的结点本事。
int minIndex = index;
while (!notCalculatedVertexes.isEmpty()) {
int minDis = Integer.MAX_VALUE;
//2、在未找到最短路径的邻接结点中找到距离最短的,记录 minDis和index(根据选择排序算法)
for (Integer res : notCalculatedVertexes) {
if ((distances[res] != -1) && distances[res] < minDis) {
minDis = distances[res];
minIndex = res;
}
}
//2.1、当未更新minDis代表其他的结点都不可达,直接跳出循环。(在无向图和网中都适应,如果是无向图那么不需要这句)
if (minDis == Integer.MAX_VALUE) break;
//3、每次循环距离最短的邻接结点的距离就是最短距离,在未找到的容器内删除。
notCalculatedVertexes.remove(minIndex);
//4、根据该 index对应的,找到根据该邻接结点到达某个结点的距离,如果更短,那么更新容器 distances[]
for (int i = (minIndex + 1) % length; i != minIndex; i = (i + 1) % length) {
if (i == index) continue;//4.1、循环过程中遇到index,代表就是最短路径,跳出本次循环。
int dis = this.edges[minIndex][i];
if ((dis != -1 && (distances[i] == -1 || minDis + dis < distances[i]))) {
distances[i] = minDis + dis;
}
}
}
return distances;
}
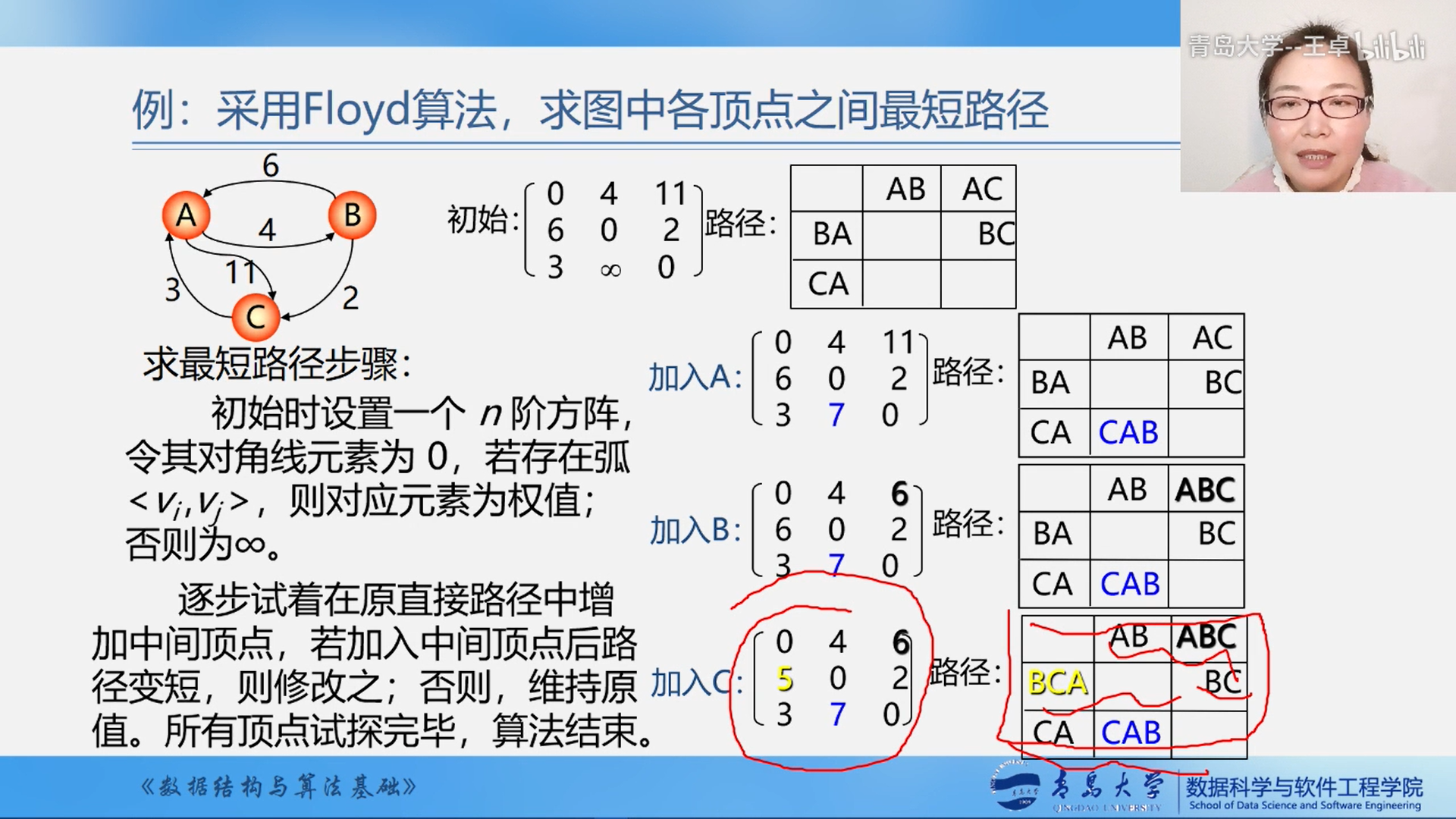
/**
* floyd解决多源之间的最小距离,时间复杂度为 O(n^3),空间复杂度为O(n^2)
*
* @return 每个顶点之间的最小距离
*/
public int[][] floyd() {
int length = this.edges.length;
//克隆edges数组,初始数据。
int[][] distances = new int[length][];
for (int i = 0; i < distances.length; i++) {
distances[i] = this.edges[i].clone();
}
//最外层循环代表每个结点都加入一次矩阵,内层的两个循环代表矩阵。
for (int k = 0; k < length; k++) {
for (int i = 0; i < length; i++) {
for (int j = 0; j < length; j++) {
if (i == j) continue; //不判断对角线
int dis = distances[i][k] + distances[k][j];
if ((dis < distances[i][j] || distances[i][j] == -1) &&
distances[i][k] != -1 && distances[k][j] != -1) {//在连通的情况下进行判断
distances[i][j] = dis;
}
}
}
}
return distances;
}
/**
* @return 生成一个简单图
*/
public static Graph buildGraph() {
String[] vertexes = {"A", "B", "C", "D", "E"};
Graph graph = new Graph(vertexes);
//添加边A-B A-C B-C B-D B-E
graph.addEdge(0, 1, 1);
graph.addEdge(0, 2, 1);
graph.addEdge(1, 2, 1);
graph.addEdge(1, 3, 1);
graph.addEdge(1, 4, 1);
return graph;
}
}
网的实现、重写了addEdge() 方法
package pri.wdw.algorithm.graph;
/**
* <p>@author wdw</p>
* <p>@date 2020/5/8 10:22</p>
* <p>@description 有向图(网) </p>
*/
public class Net extends Graph {
/**
* 有向图和无向图使用注意 :
* 无向图遍历任意一个结点都能遍历图中所有的结点(图的所有结点都是连接的)
* 在有向图当中,考虑到某些结点没有入度,会导致不能根据此结点遍历到所有的结点。
*/
public Net(String... vertexes) {
super(vertexes);
}
/**
* 有向图,v1到v2的距离
*
* @param v1 在邻接矩阵的横坐标
* @param v2 临界矩阵纵坐标
* @param weight 权值
* @return 插入是否成功
*/
@Override
public boolean addEdge(int v1, int v2, int weight) {
if (v1 < 0 || v1 >= edges.length || v2 < 0 || v2 >= edges.length || weight <= 0) {
return false;
} else {
this.edges[v1][v2] = weight;
return true;
}
}
/**
* @return 生成一个网(每个边带方向)
*/
public static Net buildNet() {
String[] vertexes = {"v0", "v1", "v2", "v3", "v4", "v5", "v6"};
Net net = new Net(vertexes);
net.addEdge(0, 1, 13);
net.addEdge(0, 2, 8);
net.addEdge(0, 4, 30);
net.addEdge(0, 6, 32);
net.addEdge(1, 5, 9);
net.addEdge(1, 6, 7);
net.addEdge(2, 3, 5);
net.addEdge(4, 5, 2);
net.addEdge(5, 6, 17);
net.addEdge(3, 4, 6);
return net;
}
public static void main(String[] args) {
Net net = Net.buildNet();
net.dfs(0);
System.out.println("-----");
net.bfs(5);
}
}
附:dijitra和flody算法图解