Spectral Normalization 谱归一化-原理及实现
//
一、谱范数及其计算方法
见我的这篇blog 谱范数求解方法-奇异值分解&幂迭代法
//
二、谱归一化提出背景
谱归一化由论文《Spectral Normalization For Generative Adversarial Networks》论文链接 提出。
原生 GAN 的目标函数等价于优化
生成数据的分布和真实数据的分布之间的J-S 散度 (Jensen–Shannon Divergence)。
而由于二者间几乎不可能有不可忽略的重叠，所以无论它们相距多远JS散度都是常数log2，最终导致生成器的梯度（近似）为0，梯度消失。
也就是说判别器训练越好，生成器梯度消失越严重。
WGAN使用性质优良的
Wasserstein distance代替原生 GAN 中的 J-S 散度。 然后利用KR对偶原理将Wasserstein distance的求解问题转换为求解最优的利普希茨连续函数的问题。 为了使得判别器 D 满足利普希茨连续性，作者使用“梯度裁剪”将过大的参数直接裁剪到一个阈值以下。
“梯度裁剪”技术从每层神经网络的参数矩阵的谱范数角度，引入利普希茨连续性约束，使神经网络对输入扰动具有较好的非敏感性，从而使训练过程更稳定，更容易收敛。(深度学习模型存在“对抗攻击样本”，比如图片只改变一个像素就给出完全不一样的分类结果，这就是模型对输入过于敏感的案例。)
我们可以这样理解：局部最小点附近如果是平坦（flatness）的话（斜率有约束），那么其泛化的性能将较好，反之，若是不平坦（sharpness）的话，稍微一点变动，将产生较大变化，则其泛化性能就不好，也就不稳定。
Spectral Norm使用一种更优雅的方式使得判别器 D 满足利普希茨连续性，限制了函数变化的剧烈程度，从而使模型更稳定。
//
三、Lipschitz 连续性
Lipschitz 条件限制的是函数变化的剧烈程度，即函数的最大梯度。
K-Lipschitz表示函数的最大梯度为K，K称为Lipschitz constant（Lipschitz常量）。例如 y = sinx的最大斜率为1，所以它是是 1-Lipschitz的。
那么：
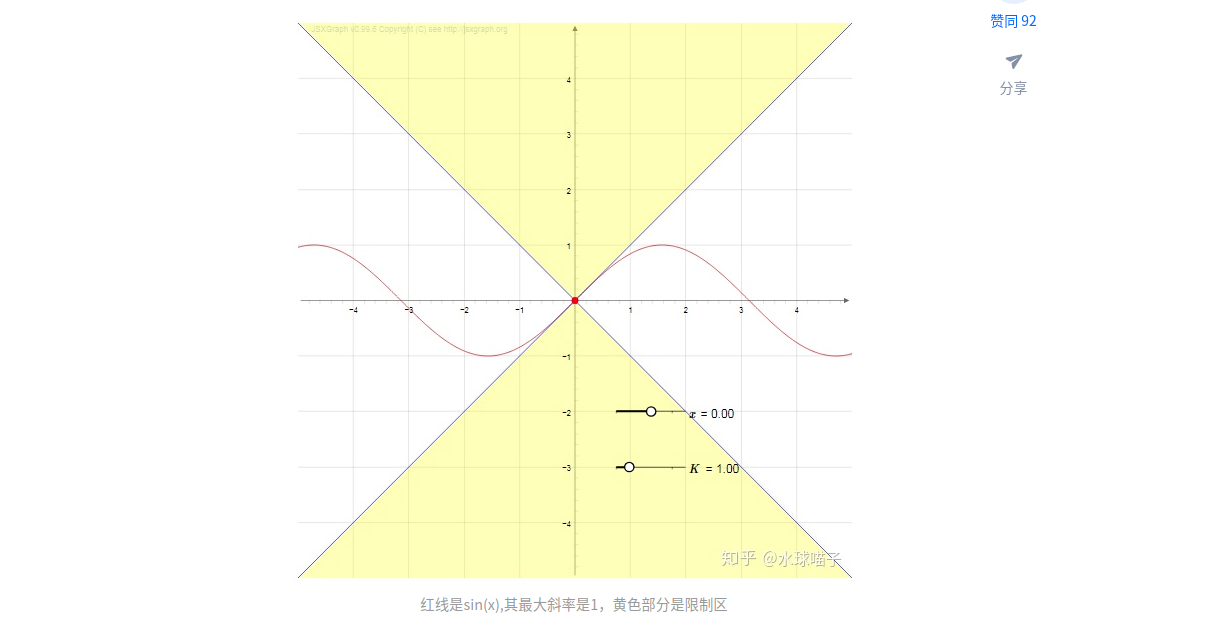
关键理论：
对矩阵A除以其谱范数可以使其具有 1-Lipschitz continuity（证明）。
//
四、GAN的谱归一化原理
对GAN做Spectral Norm，实际就是要使得判别器D满足1-Lipschitz条件。
又由于判别器D省略各个层加上的bias后，这种多层神经网络实际上是
多个复合函数嵌套的操作。
最常见的嵌套是：一层卷积，一层激活函数，再一层卷积，再一层激活函数，这样层层包裹起来。而激活函数通常选取的 ReLU，Leaky ReLU 都是 1-Lipschitz 的，我们只需要保证卷积的部分是 1-Lipschitz continuous 的（如果有Linear层也要保证Linear层是1-Lipschitz continuous 的），就可以保证整个神经网络都是 1-Lipschitz continuous 的。
那么怎样
保证卷积部分是 1-Lipschitz continuous 的呢？
图像上每个位置的卷积操作，正好可以看成是一个矩阵乘法。因此，我们只需要约束各层卷积核的参数W，使它是 1-Lipschitz continuous 的，就可以保证卷积的部分是 1-Lipschitz continuous 的，从而满足整个神经网络的 1-Lipschitz continuity。
因此，具体做法为：
对判别器D中的每一层卷积的参数矩阵W做谱归一化，即：
step 1.对W进行SVD (实现时使用幂迭代法近似代替SVD，减少计算成本)，得到W的最大奇异值。
step 2.在每一次更新W之后都除以W的最大奇异值，从而使其满足 1-Lipschitz continuity。
注意:
判别器 D 使用了 Spectral norm 之后，就不能使用 BatchNorm (或者其它 Norm) 了。 原因也很简单，因为 Batch norm 的“除方差”和“乘以缩放因子”这两个操作很明显会破坏判别器的 Lipschitz 连续性。
//
五、GAN的谱归一化实现
google用tensorflow实现了谱归一化函数链接
pytorch中有实现好的谱归一化函数
torch.nn.utils.spectral_norm（官方文档）（github）
import torch.nn as nn
import torch
# 对线性层做谱归一化
sn_module = nn.utils.spectral_norm(nn.Linear(20,40))
# 验证谱归一化后的线性层是否满足1-Lipschitz continuity
print(torch.linalg.norm(sn_module.weight,2)) # tensor(1.3898) 为啥不是1.000呢？
但是官方文档中建议使用新版谱归一化函数
torch.nn.utils.parametrizations.spectral_norm（官方文档）
不过目前看到的几乎还是用torch.nn.utils.spectral_norm的。
用法：
# #############################################################################################
# 用法1 ref: https://blog.csdn.net/qq_37950002/article/details/115592633
# #############################################################################################
import torch
import torch.nn as nn
class TestModule(nn.Module):
def __init__(self):
super(TestModule,self).__init__()
self.layer1 = nn.Conv2d(16,32,3,1)
self.layer2 = nn.Linear(32,10)
self.layer3 = nn.Linear(32,10)
def forward(self,x):
x = self.layer1(x)
x = self.layer2(x)
model = TestModule()
def add_sn(m):
for name, layer in m.named_children():
m.add_module(name, add_sn(layer))
if isinstance(m, (nn.Conv2d, nn.Linear)):
return nn.utils.spectral_norm(m)
else:
return m
my_model = add_sn(model)
# #############################################################################################
# 用法2 ref: https://github.com/Vbansal21/Custom_Architecture/EATS/models/v2_discriminator.py
# #############################################################################################
...
# 直接在卷积/线性层外面套一层nn.utils.spectral_norm()
nn.Sequential(
nn.ReflectionPad1d(7),
nn.utils.spectral_norm(nn.Conv1d(1, 16, kernel_size=15)),
nn.LeakyReLU(0.2, True),
),
...
参考 :
Spectral Normalization 谱归一化
令人拍案叫绝的Wasserstein GAN
pytorch的spectral_norm的使用
Thanks 😄
