谱范数求解方法-奇异值分解&幂迭代法

---

//

一、谱范数

矩阵的谱范数指的也就是矩阵的2范数，即矩阵A的最大奇异值。

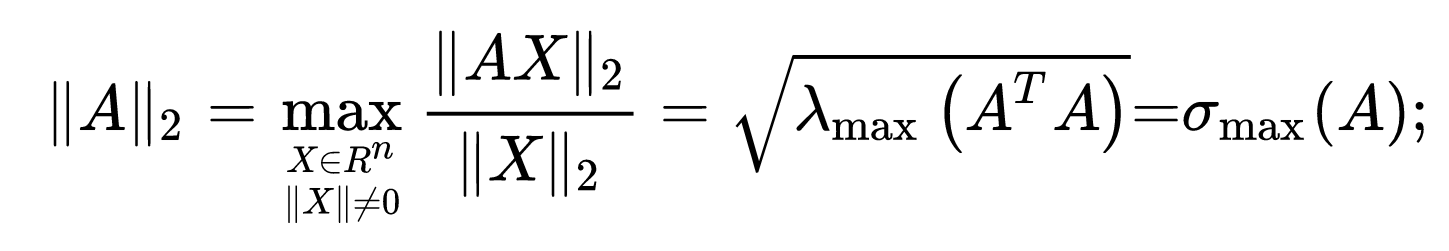
通过上式可知，A的谱范数 = A的最大奇异值 = A^T·A的最大特征值的平方根

---

//

二、谱范数求解方法

2.1 奇异值分解法 (Singular Value Decomposition)

既然谱范数是矩阵A的最大奇异值，那么便可以通过奇异值分解[举例参考]来求解谱范数。

import numpy as np

A = np.array([2,4],[1,3],[0,0],[0,0])
U, s, V = np.linalg.svd(A)

2.2 幂迭代法 (Power Iteration Method)

幂迭代法[举例参考]核心思想是通过迭代的方法来逼近真实的特征向量。

⭐STEP 1 我们首先来看如何使用幂迭代法求解矩阵A的最大特征值及其对应的特征向量。

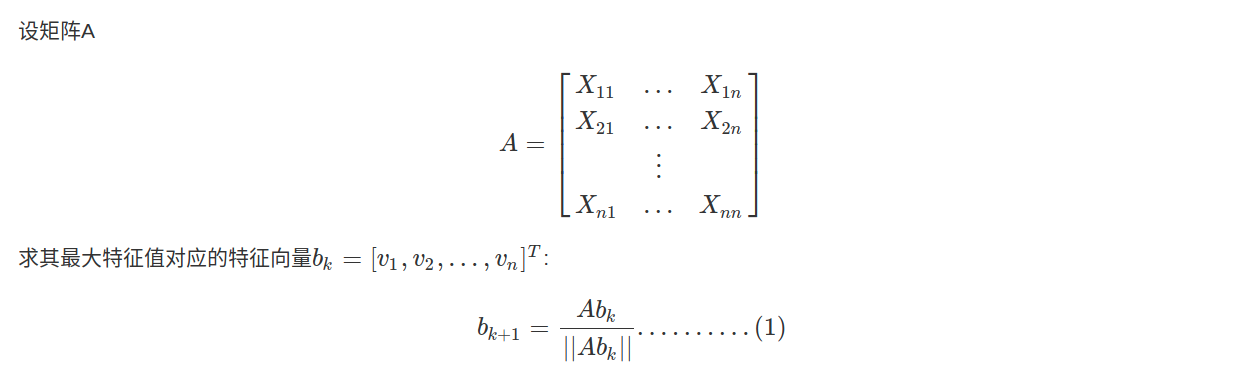
import numpy as np

def power_iteration(A, num_simulations: int):
    # Ref:https://blog.csdn.net/weixin_42973678/article/details/107801749      thanks :D
    # Ideally choose a random vector
    # To decrease the chance that our vector
    # Is orthogonal to the eigenvector
    b_k = np.random.rand(A.shape[1])

    for _ in range(num_simulations):
        # calculate the matrix-by-vector product Ab
        b_k1 = np.dot(A, b_k)

        # calculate the norm
        b_k1_norm = np.linalg.norm(b_k1)

        # re normalize the vector
        b_k = b_k1 / b_k1_norm

    return b_k

举例：

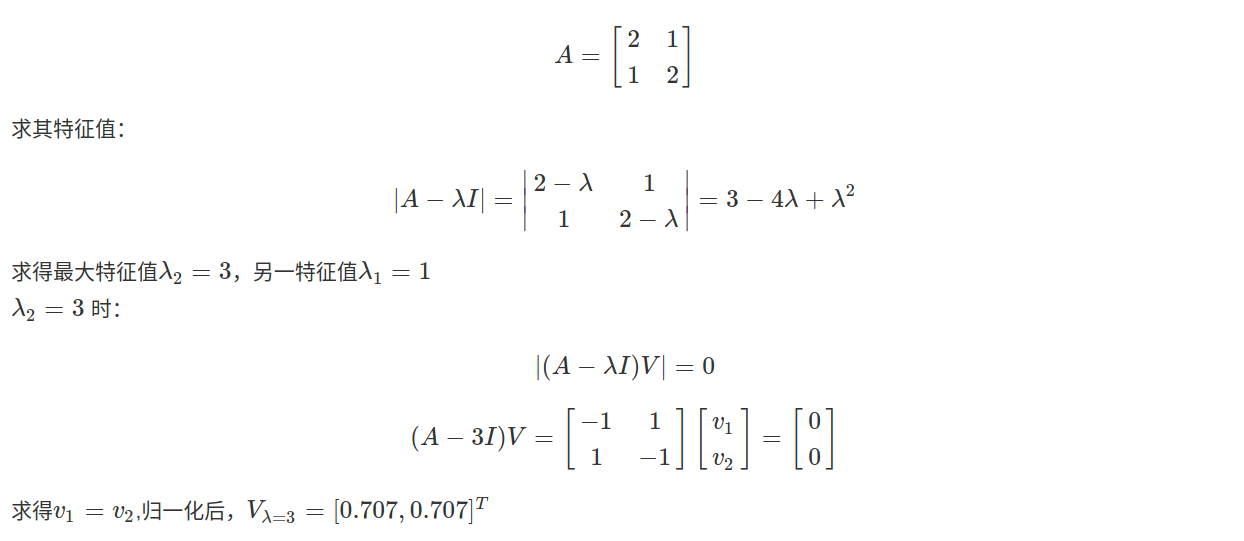
验证：

A = np.array([[2,1],[1,2]])
V = power_iteration(A, 100).reshape(1,-1)
print(V)   # array([[0.70710678, 0.70710678]])

求得最大特征值对应的特征向量后，可以通过

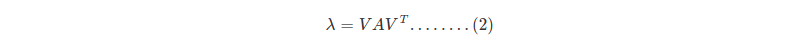
求解对应的最大特征值。

max_lambda = np.dot(V,np.dot(A,V.T))
print(max_lambda)  # array([[3.]])

⭐STEP 2 通过谱范数计算公式来计算谱范数

即通过STEP 1 的方法计算矩阵A^T·A的最大特征值和对应的特征向量，然后对最大特征值取根号，就是矩阵A的最大奇异值。

---

//

三、总结

As we mentioned above,the spectral norm σ(W) that we use to regularize each layer of the discriminator is the largest singular value of W. If we naively apply singular value decomposition to compute the σ(W) at each round of the algorithm, the algorithm can become computationally heavy. Instead, we can use the power iteration method to estimate σ(W). With power iteration method, we can estimate the spectral norm with very small additional computational time relative to the full computational cost of the vanilla GANs.
------------------------------------------------------from 《SPECTRAL NORMALIZATION FOR GENERATIVE ADVERSARIAL NETWORKS》

在计算谱范数时，SVD方法计算量大，因此使用幂迭代法可以减小计算成本。

---