Z 算法 学习笔记

问题引入

寻找字符串 \(T\) 在字符串 \(S\) 中的出现位置。

---

暴力算法

暴力枚举 \(S\) 的每一位作为开头，向后匹配，若能将 \(T\) 匹配完毕就为 \(T\) 在 \(S\) 中的一次出现。

记 \(S\) 的长度为 \(n\)，\(T\) 的长度为 \(m\)，则时间复杂度最劣为 \(O(nm)\)。

---

优化

上面的算法有很多冗余计算，具体表现在某次匹配失败就直接从下一位继续匹配，实际上在上次匹配失败的过程中，我们已经获得了 \(S\) 上后面一段的信息，可以借助此信息去掉很多无用的尝试。

比如 \(S= \text{happened}\)，\(T= \text{happy}\)，当从第一位开始匹配，到第五位失配，可以知道 \(S[1,5]= \text{happe}\) ，因此可以知道 \(T\) 不会在 \([2,4]\) 出现。

因此可以先对 \(T\) 做一些处理获得一些信息来帮助优化这种情况。

---

算法流程

将 \(T\) 和 \(S\) 中间加一个特殊符号分隔符拼在一起，记为 \(A\)，计算 \(z_i\) 表示 \(A[1,len]\) 和 \(A[i,len]\) 的 LCP 长度。

由于分隔符的存在，前 \(|T|\) 个位置的 \(z_i\) 不会等于 \(T\)，后面的位置的 \(z_i\leq |T|\)，所有 \(z_i=|T|\) 的位置刚好可以匹配成功 \(T\)，就是 \(T\) 的所有出现位置。

现在的问题就变成了如何快速计算 \(z\) 数组，显然我们希望借助前面的 \(z_i\) 的一些信息计算当前位置。

每个位置 \(i\)，\(A[i,i+z_i-1]\) 是以它开头的字符串与前缀的 LCP，定义这个字符串为 \(Z-box\)。

考虑维护 \(l,r\) 表示目前找到的最靠右（右端点最大）的 \(Z-box\) 左右端点，此时已知 \(z_{1}-z_{i-1}\)，要求 \(z_i\)，分为以下几种情况：

1. \(i>r\)，直接从 \(i\) 开始暴力匹配前缀，\(z_i\) 为匹配的长度，\(l,r\) 更新为 \(i,i+z_i-1\)。

2. \(i \leq r\)
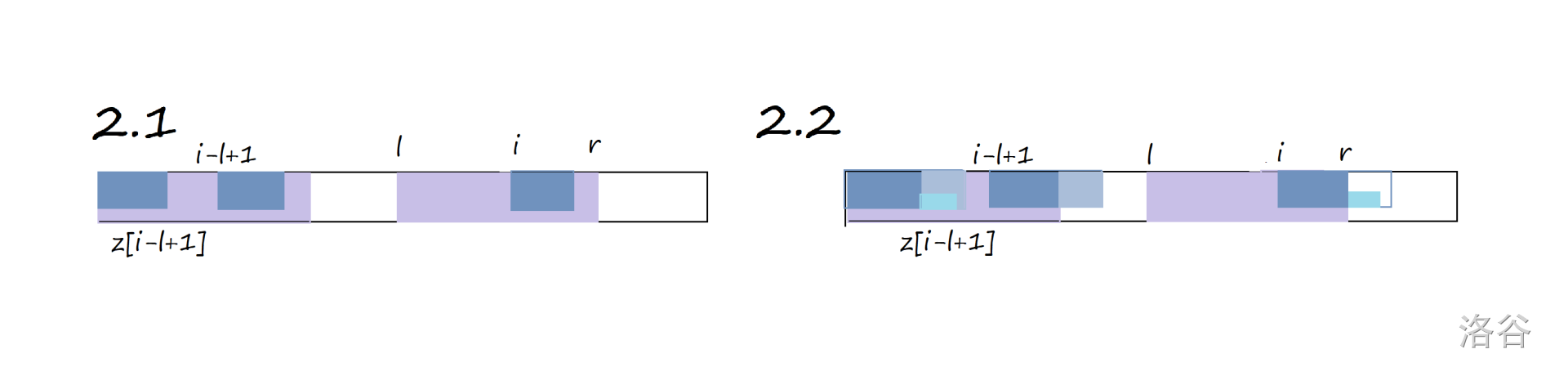
   2.1 \(z_{i-l+1} \leq r-i+1\)，\(z_i=z_{i-l+1}\)，\(l,r\) 不变。
   2.2 \(z_{i-l+1} > r-i+1\)，先令 \(z_i=r-i+1\) ，然后继续匹配前缀更新 \(z_i\)，并将 \(l,r\) 更新为 \(i,i+z_i-1\)。

情况二的解释如下图（图自己画的有点丑）：

---

复杂度分析

首先需要从头到尾扫一遍字符串。

在不用暴力匹配的时候，直接计算是单次 \(O(1)\)，如果需要暴力匹配一定会向右移动 \(r\)，且 \(r\) 的移动是单调的，因此 \(r\) 移动（即暴力匹配）的总时间是 \(O(n)\) 的。

因此这个匹配算法是线性的。

---

代码

z[1]=n
for(int i=2;i<=n;++i){
  if(i<=r) z[i]=min(z[i-l+1],r-i+1);
  while(i+z[i]<=n&&s[i+z[i]]==s[z[i]+1]) ++z[i];
  if(i+z[i]-1>r) l=i,r=i+z[i]-1;
}