[总结]最近公共祖先(倍增求LCA)
一、定义
给定一颗有根树,若节点z既是节点x的祖先,也是节点y的祖先,则称z是x,y的公共祖先。在x,y的祖先中,深度最大的一个节点称为x,y的最近公共祖先(Least Common Ancestors),记做LCA。
如图:LCA(5,7)=2;LCA(3,8)=1;LCA(6,10)=6。
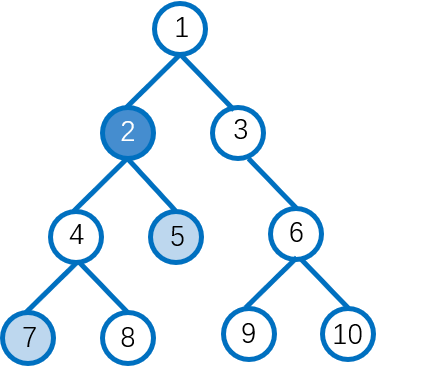
二、LCA的实现流程
LCA一共有三种可以实现的方法:
- 向上标记法
- 倍增法
- Tarjan算法(方法一的优化)
当然我们最熟悉不过的还是倍增法求LCA。
1. 预处理
在引入倍增优化之前,我们先来看看寻找两点LCA的朴素做法。
以寻找节点5,节点2的LCA为例:
首先求出每个点的深度,dep[7]=4,dep[5]=3。
我们先从深度大的节点7开始向上跳,直到深度和5一致,即跳到了节点4,此时这两个节点还没有到同一个点。
接下来我们继续让节点4和节点5向上跳,当他们跳到节点2的时候,由于跳到了相同节点,因此确定节点2是节点7,节点5的LCA。
显然,对于这样暴力的做法,速度慢的原因在于每一次只向上方跳一步,想要加快向上跳的速度,就需要采用倍增法进行优化。
我们设fa[x,k]表示x向上跳\(2^k\)的祖先节点,特别地,fa[x,0]就是x的父亲节点。
fa数组可以通过递推得出,x节点向上跳\(2^k\)步可以由x向上跳\(2^{k-1}\)步再向上跳\(2^{k-1}\)步推出。
递推方程:
或者
fa数组可以在遍历的时候求出,该预处理操作的总复杂度为\(O(NlogN)\)。
下面给出预处理的模板:
inline void Deal_first(int u,int fath){
dep[u]=dep[fath]+1;
fa[u][0]=fath;
for(int i=0;i<20;i++) fa[u][i+1]=fa[fa[u][i]][i];//递推过程
for(int e=first[u];e;e=next[e]){
int v=go[e];
if(v==fath) continue;
Deal_first(v,u);
}
}
2. 计算LCA
借助倍增优化计算x,y的LCA共需要跳logn步,因此时间复杂度为\(O(logN)\)。
我们首先需要将深度大的节点向上跳,直到两个节点深度相同,设dep[ ]表示每个节点的深度,若\(dep[x]\leq dep[y]\),我们交换节点x,节点y(swap(x,y))使得节点x深度最大,此时我们将x向上调整到与y同一深度。操作完成后判断节点x是否等于节点y,如果相等,则说明LCA(x,y)=y,即x,y在一条链上,我们在此返回y即可。
当x,y跳到同一层后,我们利用二进制拆分思想,依次向上跳\(2^{logn},2^{logn-1},...,2^2,2^1,2^0\)步,同时让x,y向上调整并保证他们跳\(2^k\)步的父节点不相等(两个节点不相遇)。
循环结束后,x的父节点fa[x][0]就是节点x,y的LCA。
下面给出求LCA的模板:
int LCA(int x,int y){
if(dep[x]<dep[y]) swap(x,y);//减少代码长度,为了方便我们总让x先跳
for(int i=20;i>=0;i--){//必须倒序循环,要证明正确性很简单,这里就不给具体证明过程了
if(dep[fa[x][i]]>=dep[y]) x=fa[x][i];
}
if(x==y) return y;
for(int i=20;i>=0;i--){
if(fa[x][i]!=fa[y][i]){
x=fa[x][i];y=fa[y][i];
}
}
return fa[x][0];
}
三、例题
例1:P3379 【模板】最近公共祖先(LCA)
Code:
#include<bits/stdc++.h>
#define re register
using namespace std;
int first[1000010],next[1000010],go[1000010],tot;
int dep[1000010],fa[1000010][22];
inline void read(int &x){
x=0;int flag=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') flag=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=x*10+ch-'0';
ch=getchar();
}
x=x*flag;
}
inline void add_edge(int u,int v){
next[++tot]=first[u];
first[u]=tot;
go[tot]=v;
}
inline void Deal_first(int pre,int u){
dep[u]=dep[pre]+1;
fa[u][0]=pre;
for(re int i=0;i<20;i++) fa[u][i+1]=fa[fa[u][i]][i];
for(re int e=first[u];e;e=next[e]){
int v=go[e];
if(v==pre) continue;
Deal_first(u,v);
}
}
int LCA(int x,int y){
if(dep[x]<dep[y]) swap(x,y);
for(re int i=20;i>=0;i--){
if(dep[fa[x][i]]>=dep[y])
x=fa[x][i];
if(x==y) return y;
}
for(re int i=20;i>=0;i--){
if(fa[x][i]!=fa[y][i]){
x=fa[x][i];
y=fa[y][i];
}
}
return fa[x][0];
}
int main()
{
int m,n,s,u,v;
read(n),read(m),read(s);
for(re int i=1;i<=n-1;i++){
read(u),read(v);
add_edge(u,v);add_edge(v,u);
}
Deal_first(0,s);
int a,b;
for(re int i=1;i<=m;i++){
read(a),read(b);
printf("%d\n",LCA(a,b));
}
return 0;
}
四、树上差分
差分思想我们已经在树状数组的那篇文章中(原文链接)提及,差分与树上差分的区别在于:差分在序列上操作,而树上差分则在一棵树上进行操作。
树上差分可以解决树上一段连续区间的权值更改问题。
分类:树上差分分为点差分和边差分两类。
1. 边差分
边差分修改一段连续区间的边权。
以节点x到节点y的最短路径上的边权都加1为例:
其中,fa[ ]数组表示任意节点的父节点。
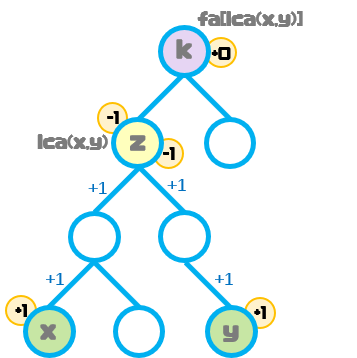
我们设数组p[ ]表示每个节点的点权,因此得到p[x]+=1,p[y]+=1。
由于x,y的最近公共祖先节点z的点权不受边权的改变而改变,因此可以得出p[z]-=2,即x,y的贡献均到节点z结束。
这样节点z及以上节点都能保证正确性。
最终的操作为:p[x]++; p[y]++; p[lca(x,y)]-=2;
2. 点差分
点差分修改一段连续区间的点权。
我们同样以节点x到节点y的最短路径上的点权都加1为例:
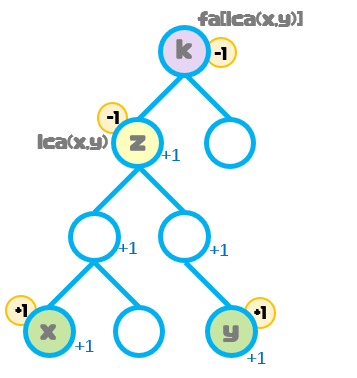
我们不难发现,点差分中节点x,节点y的差分数组是没有变化的,仍为p[x]+=1,p[y]+=1。
由于修改的是点权,此时的节点z也会加一个点权,如果我们按照边差分的方式处理节点z,那么就相当于节点z没有被影响到,也就是说点z的点权没有变化。
由于点z子树内的节点会对它贡献两次答案,因此我们只在节点z的差分数组里减1,就可以只一个贡献答案。
此时我们的操作还没有结束,因为点z的差分数组中仍+1,即z会对它的祖先节点产生影响。
我们只需要在点z的父节点k的差分数组中减去1就能消除影响。
最终的操作为:p[x]++; p[y]++; p[lca(x,y)]--;p[fa[lca(x,y)]]--;
3. 例题
P3128 [USACO15DEC]最大流Max Flow
点差分的模板题。
Code:
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#define N 100010
#define INF 0x7fffffff
using namespace std;
int n,m,tot,ans=-INF;
int fa[N<<2][22],dep[N<<2],p[N<<1];
int first[N<<1],nxt[N<<1],go[N<<1];
inline void add_edge(int u,int v){
nxt[++tot]=first[u];
first[u]=tot;
go[tot]=v;
}
void Deal_first(int u,int fath){
dep[u]=dep[fath]+1;
fa[u][0]=fath;
for(int i=0;i<20;i++)
fa[u][i+1]=fa[fa[u][i]][i];
for(int e=first[u];e;e=nxt[e]){
int v=go[e];
if(v==fath) continue;
Deal_first(v,u);
}
}
int LCA(int x,int y)
{
if(dep[x]<dep[y]) swap(x,y);
for(int i=20;i>=0;i--){
if(dep[fa[x][i]]>=dep[y])
x=fa[x][i];
if(x==y) return x;
}
for(int i=20;i>=0;i--){
if(fa[x][i]!=fa[y][i]){
x=fa[x][i];
y=fa[y][i];
}
}
return fa[x][0];
}
void DFS_get_path(int u,int fath){
for(int e=first[u];e;e=nxt[e]){
int v=go[e];
if(v==fath) continue;
DFS_get_path(v,u);
p[u]+=p[v];//该点影响由自己以及子树中的节点贡献
}
ans=max(ans,p[u]);//求最大压力
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<n;i++){
int u,v;
scanf("%d%d",&u,&v);
add_edge(u,v);
add_edge(v,u);
}
Deal_first(1,0);
for(int i=1;i<=m;i++){
int x,y;
scanf("%d%d",&x,&y);
int lca=LCA(x,y);
p[x]++;p[y]++;//树上差分的核心
p[lca]--;
p[fa[lca][0]]--;
}
DFS_get_path(1,0);
printf("%d",ans);
return 0;
}


