[总结]数据结构-线段树
目录
一、关于线段树
线段树(Segment tree)是一种可以完成区间操作的二叉树结构,其应用范围较树状数组更广。
线段树采用分治思想,每一个节点都代表一个区间,一棵完整的线段树除去最后一层深度为\(O(logN)\),由于最底层非空,因此数组需要开到\(4N\)(静态线段树)。
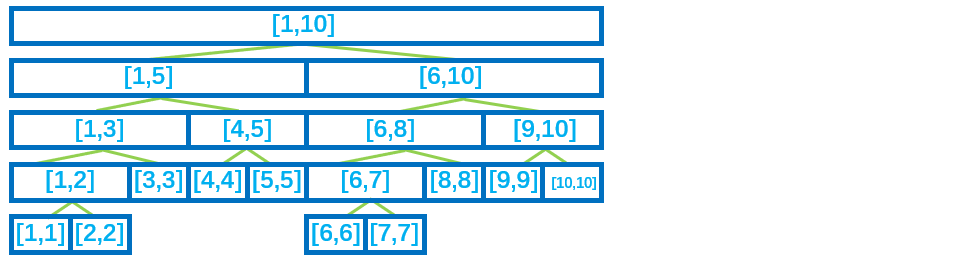
如果线段树的内部节点\(x\)代表\([l,r]\),那么\(x\)的左子节点\(2\times x\)代表\([l,mid]\),\(x\)的右子节点\(2\times x+1\)代表\([mid+1,r]\),其中\(mid=(l+r)>>1\)。
二、线段树的实现
线段树的操作包括单点修改,区间修改,区间查询。
1. 建树
void build(int k,int l,int r){
if(l==r){//叶子节点
sum[k]=a[l];
return;
}
int mid=(l+r)>>1;
build(k<<1,l,mid);//遍历左子节点
build(k<<1|1,mid+1,r);//遍历右子节点
sum[k]=sum[k<<1]+sum[k<<1|1];//求区间和
//maxn[k]=max(maxn[k<<1],maxn[k<<1|1]);求区间最大值
}
build(1,1,n);//主函数内
2. 单点修改
void modify(int k,int l,int r,int pos,int val){
if(l==r){
sum[k]+=val;
return;//一定不要忘了回溯
}
int mid=(l+r)>>1;
if(pos<=mid) modify(k<<1,l,mid,pos,val);
else modify(k<<1|1,mid+1,r,pos,val);
sum[k]=sum[k<<1]+sum[k<<1|1];//push_up操作,回溯时更新节点权值
}
modify(1,1,n,要修改的点,点权);//主函数内
2. 区间查询(以询问区间和为例)
int query(int k,int l,int r,int L,int R){
if(l>=L&&r<=R) return sum[k];//节点范围在遍历区间内
if(l>R||r<L) return 0;//在区间外,可以不写
int mid=(l+r)>>1,res=0;
if(mid>=L) res+=query(k<<1,l,mid,L,R);
if(mid<R) res+=query(k<<1|1,mid+1,r,L,R);
return res;
}
query(1,1,n,要询问的左区间,右区间);//主函数内
3. 区间修改
区间修改需要用到延迟标记(又叫做懒惰标记,Lazy_tag),延迟标记的具体原理是什么呢?当我们在执行修改操作的时候,满足 l>=L&&r<=R 时我们同样回溯,并在回溯前标记\(lazy[k]=val\),表示该点已经修改,但是没有更新它的子节点。做完标记以后,当我们再次访问这个点的时候(后续的操作),我们检查\(k\)是否有延迟标记,如果有标记,那么更新两个子节点的权值并为这两个点同样打上延迟标记,最后删除\(k\)点的标记。
延迟标记:
void pushdown(int k,int l,int r,int mid){
if(lazy[k]==0) return;
lazy[k<<1]+=lazy[k];//标记下传
sum[k<<1]+=lazy[k]*(mid-l+1);//更新左节点
lazy[k<<1|1]+=lazy[k];
sum[k<<1|1]+=lazy[k]*(r-mid);//更新右节点
lazy[k]=0;//清除标记
}
push_down(k,l,r,mid);//在modify() 和 query() 函数中
//另外,modify()函数中在即将回溯时改为:
if(l>=L&&r<=R){
lazy[k]+=val;
sum[k]=val*(r-l+1);
return;
}
三、动态开点线段树
当数据十分分散并且范围很大时,数组已经无法开到\(4N\)的大小,这时我们建立动态开点线段树可以解决该问题,最终数组只需要开到\(2N\)。
动态开点线段树也十分简单,初始不用建树,建立两个数组lson,rson代表节点的左子节点,右子节点。
- 在更改权值时,若这个点没有被编号,说明没有这个点,那么此时给这个点增加一个编号。
- 查询时若节点编号为0,那么直接回溯即可。
- 若涉及延迟标记,在更新左/右节点时,如果左右节点编号为0,那么新建节点。
Code:
区间修改,区间查询。
#include<bits/stdc++.h>
#define maxn 10001000
using namespace std;
int n,m,root=1,cnt=1;
int lson[maxn],rson[maxn];
int lazy[maxn<<2],sum[maxn<<2];
inline int Find_id(int &pos){
if(pos==0) pos=++cnt;
return pos;
}
void Push_up(int pos){
sum[pos]=sum[lson[pos]]+sum[rson[pos]];
}
inline void Push_down(int pos,int l,int r)//区间查询用
{
int mid=(l+r)>>1;
sum[Find_id(lson[pos])]+=(mid-l+1)*lazy[pos];
sum[Find_id(rson[pos])]+=(r-mid)*lazy[pos];
lazy[lson[pos]]+=lazy[pos];
lazy[rson[pos]]+=lazy[pos];
lazy[pos]=0;
}
void Update(int &pos,int l,int r,int L,int R,int C)
{
//L,R表示操作区间 , l,r表示当前节点区间 , pos表示当前节点编号
if(pos==0) pos=++cnt;
if(lazy[pos]!=0) Push_down(pos,l,r);
if(L<=l&&R>=r)//节点区间在操作区间之内,直接返回
{
sum[pos]+=(r-l+1)*C;//这个点需要加上区间长度*C
lazy[pos]+=C;//用Lazy标记,表示本区间的Sum正确,子区间的Sum仍需要根据Lazy调整
return;
}
int mid=(l+r)>>1;
if(L<=mid) Update(lson[pos],l,mid,L,R,C);
if(R>mid) Update(rson[pos],mid+1,r,L,R,C);
Push_up(pos);
}
int query(int pos,int l,int r,int L,int R)
{
//L,R表示操作区间 , l,r表示当前节点区间 , pos表示当前节点编号
if(pos==0) return 0;
if(lazy[pos]) Push_down(pos,l,r);//下推标记,否则sum可能不正确
if(L<=l&&R>=r)
return sum[pos];
long long ans=0;
int mid=(l+r)>>1;
if(L<=mid) ans+=query(lson[pos],l,mid,L,R);
if(R>mid) ans+=query(rson[pos],mid+1,r,L,R);
Push_up(pos);
return ans;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
int temp;
scanf("%d",&temp);
Update(root,1,n,i,i,temp);
}
for(int i=1;i<=m;i++)
{
int flag,x,y,k;
scanf("%d",&flag);
if(flag==1){
scanf("%d%d%d",&x,&y,&k);
Update(root,1,n,x,y,k);
}
else{
scanf("%d%d",&x,&y);
printf("%lld\n",query(root,1,n,x,y));
}
}
return 0;
}
四、例题
例1:P3372 【模板】线段树 1
区间修改与区间查询,注意开long long。
Code:
#include<bits/stdc++.h>
#define ll long long
const ll N=1e5+5;
ll n,m,a[N],lazy[N<<2],sum[N<<2];
inline int read(){
char ch=getchar();int flag=1,x=0;
while(!isdigit(ch)){if(ch=='-') flag=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return x*flag;
}
inline void build(ll k,ll l,ll r){
if(l==r){
sum[k]=a[l];return;
}
ll mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
sum[k]=sum[k<<1]+sum[k<<1|1];
}
inline void pushdown(ll k,ll l,ll r,ll mid){
if(lazy[k]==0) return;
lazy[k<<1]+=lazy[k];lazy[k<<1|1]+=lazy[k];
sum[k<<1]+=lazy[k]*(mid-l+1);
sum[k<<1|1]+=lazy[k]*(r-mid);
lazy[k]=0;
}
inline ll query(ll k,ll l,ll r,ll L,ll R){
if(l>=L&&r<=R) return sum[k];
ll mid=(l+r)>>1,res=0;
pushdown(k,l,r,mid);
if(L<=mid) res+=query(k<<1,l,mid,L,R);
if(mid<R) res+=query(k<<1|1,mid+1,r,L,R);
return res;
}
inline void modify(ll k,ll l,ll r,ll L,ll R,ll val){
if(l>=L&&r<=R){
sum[k]+=val*(r-l+1);
lazy[k]+=val;
return;
}
ll mid=(l+r)>>1;
pushdown(k,l,r,mid);
if(L<=mid) modify(k<<1,l,mid,L,R,val);
if(mid<R) modify(k<<1|1,mid+1,r,L,R,val);
sum[k]=sum[k<<1]+sum[k<<1|1];
}
int main()
{
n=read(),m=read();
for(int i=1;i<=n;i++) a[i]=read();
build(1,1,n);
while(m--){
int op=read(),A,B,C;
if(op==1){
A=read(),B=read(),C=read();
modify(1,1,n,A,B,C);
}
if(op==2){
A=read(),B=read();
printf("%lld\n",query(1,1,n,A,B));
}
}
return 0;
}
例2:P3373 【模板】线段树 2
懒标记时优先更新乘法,再更新加法,其他同例1。
Code:(动态开点线段树)
#include<bits/stdc++.h>
#define ll long long
#define N 400100
using namespace std;
int m,n,mod,root=1,cnt=1;
int lson[N],rson[N];
ll val[N],lazy_mul[N<<2],lazy_plu[N<<2];
inline int Find_id(int &pos){
if(pos==0) pos=++cnt;
return pos;
}
void Push_down(int pos,int l,int r){
int mid=(l+r)>>1;
val[Find_id(lson[pos])]=(val[Find_id(lson[pos])]*lazy_mul[pos]+lazy_plu[pos]*(mid-l+1))%mod;
val[Find_id(rson[pos])]=(val[Find_id(rson[pos])]*lazy_mul[pos]+lazy_plu[pos]*(r-mid))%mod;
lazy_mul[lson[pos]]=(lazy_mul[lson[pos]]*lazy_mul[pos])%mod;
lazy_mul[rson[pos]]=(lazy_mul[rson[pos]]*lazy_mul[pos])%mod;
lazy_plu[lson[pos]]=(lazy_plu[lson[pos]]*lazy_mul[pos]+lazy_plu[pos])%mod;
lazy_plu[rson[pos]]=(lazy_plu[rson[pos]]*lazy_mul[pos]+lazy_plu[pos])%mod;
lazy_mul[pos]=1;
lazy_plu[pos]=0;
return;
}
inline void Push_up(int pos){
val[pos]=(val[lson[pos]]+val[rson[pos]])%mod;
}
void Update_mul(int &pos,int l,int r,int L,int R,int k){
if(!pos) pos=++cnt;
//if(lazy_mul[pos]!=1)
Push_down(pos,l,r);
if(l>R||r<L) return;
if(l>=L&&r<=R){
val[pos]=(val[pos]*k)%mod;
lazy_mul[pos]=(lazy_mul[pos]*k)%mod;
lazy_plu[pos]=(lazy_plu[pos]*k)%mod;
return;
}
int mid=(l+r)>>1;
if(L<=mid) Update_mul(lson[pos],l,mid,L,R,k);
if(R>mid) Update_mul(rson[pos],mid+1,r,L,R,k);
Push_up(pos);
}
void Update_plu(int &pos,int l,int r,int L,int R,int k){
if(!pos) pos=++cnt;
//if(lazy_plu[pos]!=0)
Push_down(pos,l,r);
if(l>R||r<L) return;
if(L<=l&&R>=r){
lazy_plu[pos]=(lazy_plu[pos]+k)%mod;
val[pos]=(val[pos]+k*(r-l+1))%mod;
return;
}
int mid=(l+r)>>1;
if(L<=mid) Update_plu(lson[pos],l,mid,L,R,k);
if(R>mid) Update_plu(rson[pos],mid+1,r,L,R,k);
Push_up(pos);
}
int query(int pos,int l,int r,int L,int R)
{
if(pos==0) return 0;
if(l>R||r<L) return 0;
if(L<=l&&R>=r) return val[pos];
Push_down(pos,l,r);
ll ans=0;
int mid=(l+r)>>1;
if(L<=mid) ans=(ans+query(lson[pos],l,mid,L,R))%mod;
if(R>mid) ans=(ans+query(rson[pos],mid+1,r,L,R))%mod;
return ans%mod;
}
int main()
{
memset(lazy_mul,1,sizeof(lazy_mul));
scanf("%d%d%d",&n,&m,&mod);
for(int i=1;i<=n;i++){
int ord;
scanf("%d",&ord);
Update_plu(root,1,n,i,i,ord);
}
for(int i=1;i<=m;i++){
int flag,x,y,k;
scanf("%d",&flag);
if(flag==1){//multiple
scanf("%d%d%d",&x,&y,&k);
Update_mul(root,1,n,x,y,k);
}
if(flag==2){//plus
scanf("%d%d%d",&x,&y,&k);
Update_plu(root,1,n,x,y,k);
}
if(flag==3){
scanf("%d%d",&x,&y);
printf("%lld\n",query(root,1,n,x,y));
}
}
return 0;
}

吸爆Rufen!

