[总结]树与图的遍历
一、图的深度优先遍历
图的深度优先遍历,就是在遍历到一个点\(x\)时任取一条边继续遍历,直到回溯到\(x\),再考虑走其他的边。
图的深度优先遍历会访问每个点,每条边各一次(无向图正反边各访问一次),故时间复杂度为\(O(N+M)\)。
利用图的深度优先遍历可以统计图或树上的各种信息。
具体实现:
void dfs(int u){
vis[u]=1;
for(int i=first[u];e;e=next[e]){
int v=go[e];
if(vis[v]) continue;
dfs(v);
}
}
1.时间戳
我们对图按照深度优先遍历的时候,以每次访问到的节点的顺序标记(也可以理解为vis[u]被标记成1的时候),这样的标记就是时间戳,通常用\(dfn[ ]\)表示。
具体实现:
void dfs(int u){
vis[u]=1;
dfn[u]=dfn[0]++; //默认节点编号为1~n
for(int i=first[u];e;e=next[e]){
int v=go[e];
if(vis[v]) continue;
dfs(v);
}
}
2.树的DFS序
当我们对树进行深度优先遍历时,我们分别在一个点递归开始和递归结束(即将回溯)时各记录一次这个节点的编号,最后产生长度为2N的序列就是树的DFS序。
特点:
设一个点\(x\)在DFS序中出现的位置分别为\(L,R\),那么[L,R]就是以\(x\)为根结点的子树的DFS序,这样就可以把对子树的操作转化为在序列上操作。
具体实现:
void dfs(int u){
vis[u]=1;
num[++cnt]=u;
for(int i=first[u];e;e=next[e]){
int v=go[e];
if(vis[v]) continue;
dfs(v);
}
num[++cnt]=u;
}
3.树的深度
一棵树的深度就是根结点到叶子节点的最大距离,我们在遍历每个点时,不断递推子节点高度。
最初,根结点的深度为0,每次遍历都有\(dep[v]=dep[u]+1;\),这样可以求出每个点的深度。
具体实现:
void dfs(int u){
vis[u]=1;
for(int i=first[u];e;e=next[e]){
int v=go[e];
if(vis[v]) continue;
dep[v]=dep[u]+1;
dfs(v);
}
}
4.树的重心
正如字面意思,我们要寻找这样一个节点,使得树的左右两边尽量平衡。平衡意味着我们要找到这样一个节点:
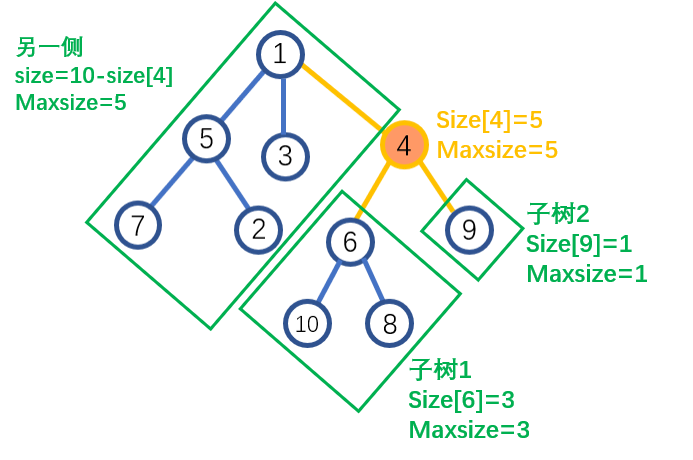
它最大的子树的大小要小于任意其他节点的最大子树的大小。
我们任选一个节点作为我们树的重心,这时求出该节点最大子树的大小\(maxsize\),并记录着个节点为答案。如果之后遍历的节点能够使\(maxsize\)减小,那么这个点作为重心一定更优,因此我们更新\(maxsize\),以及最终答案。
具体实现:
void dfs(int u){
vis[u]=1;size[u]=1;//只有一个点的大小为1
for(int i=first[u];e;e=next[e]){
int v=go[e];
if(vis[v]) continue;
dfs(v);
size[u]+=size[v];//在回溯的时候(由下至上)更新根结点的子树大小
maxsize=max(size[v],maxsize);//目前节点最大子树的大小,对应"子树1","子树2"
}
maxsize=max(maxsize,n-size[u]);//更新其余部分的大小
if(maxsize<ansize){//如果产生更小的最大子树
ansize=maxsize;//更新最小的最大子树大小
pos=u;//记录这个点
}
}
5.树的直径
树的直径就是一棵树中任意两点的最远距离。要求树的直径,可以先从根结点遍历,找到最远的一个节点,再由这个节点作为根结点进行遍历就能求出这棵树的直径。我们可以知道,该直径的两端点必然是树的两个叶子节点。
具体实现:
#include<bits/stdc++.h>
#define N 5000
struct node{
int next,to;
}edge[N];
int num_edge,head[N],dis[N],n,a,b,y;
inline void add_edge(int from,int to){
edge[++num_edge].next=head[from];
edge[num_edge].to=to;
head[from]=num_edge;
}
int dfs(int x){
for(int i=head[x];i;i=edge[i].next)
if(!dis[edge[i].to]){
dis[edge[i].to]=dis[x]+1;
dfs(edge[i].to);
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<n;++i){
scanf("%d%d",&a,&b);
add_edge(a,b);add_edge(b,a);
}
dfs(1);
for(int i=y=1;i<=n;i++) if(dis[i]>dis[y]) y=i;
memset(dis,0,sizeof(dis));
dfs(y);
for(int i=y=1;i<=n;i++) if(dis[i]>dis[y]) y=i;
printf("%d",dis[y]);
return 0;
}
二、图的广度优先遍历
图的深度优先遍历会沿着一条边走并回溯,而广度遍历会将该节点能到达的所有的节点全部插入队列(已访问过的除外),直到队列为空。
性质:
- 队列里只会保存第\(x\)层和第\(x+1\)层的节点。
- 只有第\(x\)层节点遍历完以后,才会遍历第\(x+1\)层的节点。
具体实现:
void bfs(){
queue<int> q;
q.push(1);
while(!q.empty()){
int u=q.front();q.pop();
vis[u]=1;
for(int i=first[u];i;i=next[i]){
int v=go[i];
if(vis[v]) continue;
vis[v]=1;
q.push(v);
}
}
}
三、练习
P2986 [USACO10MAR]伟大的奶牛聚集
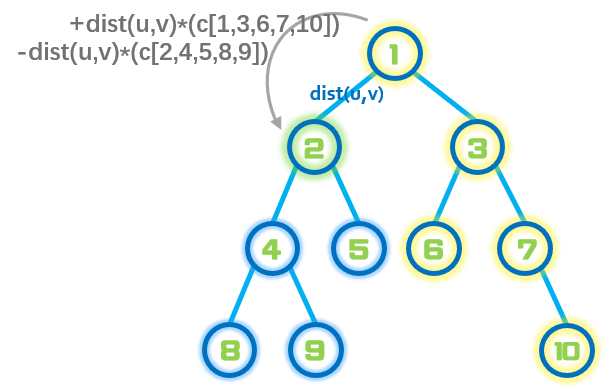
首先计算所有牛到根结点所用的路程之和,之后依次推出到其他节点的路程。
由原来集合的节点u到节点v所走的路程变化为:
少走了\(cow[u]×dist[u]\) (u的子树节点的牛的个数×由u到v的路径长度),多走了\((all-cow[u])*dist[u]\)(其余节点牛的个数×由u到v的路径长度)。
Code:
#include<bits/stdc++.h>
#define N 200010
#define ll long long
const ll INF=0x3f3f3f3f3f3f3f3f;
using namespace std;
int n,all,c[N];
int tot,first[N<<1],nxt[N],go[N],cost[N];
ll cow[N],Ans=INF,dist[N],sum[N],ans[N];
inline void add_edge(int u,int v,int w){
nxt[++tot]=first[u];
first[u]=tot;
go[tot]=v;
cost[tot]=w;
}
inline void calc_sum(int u,int fath){
cow[u]=c[u];//节点u的子树中牛的数量
for(int e=first[u];e;e=nxt[e]){
int v=go[e],w=cost[e];
if(v==fath) continue;
dist[v]=w;//记录u,v的边权
calc_sum(v,u);
cow[u]+=cow[v];
sum[u]+=sum[v]+w*cow[v];//求出子树中所有奶牛到节该点的路程
}
}
inline void calc_ans(int u,int fath){
if(u==1) ans[u]=sum[u];//从根结点扩展
else ans[u]=ans[fath]+(all-cow[u])*dist[u]-cow[u]*dist[u];//计算左右牛到节点u的路程
for(int e=first[u];e;e=nxt[e]){
int v=go[e];
if(v==fath) continue;
calc_ans(v,u);
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&c[i]);
all+=c[i];//求出所有奶牛的数量
}
for(int i=1,u,v,w;i<n;i++){
scanf("%d%d%d",&u,&v,&w);
add_edge(u,v,w);
add_edge(v,u,w);
}
calc_sum(1,0);//计算所有牛到根结点的路程
calc_ans(1,0);//求出所有牛到树上每一个点的路程
for(int i=1;i<=n;i++) Ans=min(Ans,ans[i]);
printf("%lld",Ans);
return 0;
}



