复数
复数
虚数定义
英文名称是imageinary number, 表示虚构的数或者不存在的数。其定义为\(i = \sqrt{-1}\)。
在实数域中，\(\sqrt{-1}\)是没有意义的也不存在。虚数在现实世界并没有实际含义，并不像在实数域中那样，比如实数2，可以表示2个苹果，2只羊，或者2厘米等。但虚数如2i，在现实物理实际中，是无法找到与之对应的。
虚数/复数发展历史
参考维基百科-虚数/复数
- 最早提到有关负数的平方根的文献是公元1世纪古希腊数学家亚历山大的希罗，他考虑的是一种不可能的平顶金字塔的域积，计算结果会是\(\sqrt{81-144}=3i\sqrt{7}\)
- 16世纪意大利数学家（请参看塔塔利亚和卡尔达诺）得出一元三次和四次方程式的根的表达式，并发现即使只考虑实数根，仍不可避免面对负数方根。
- 17世纪笛卡尔称负数方根为虚数，“子虚乌有的数”，表达对此的无奈和不忿。
- 18世纪初棣莫弗及欧拉大力推动复数的接受。1730年，棣莫弗提出棣莫弗公式：\((cos\theta + isin\theta)^n = cos\ n\theta + isin\ n\theta\)。而欧拉则在1748年提出了著名的欧拉公式\(e^{i\theta} = cos\theta + i sin \theta\)
- 18世纪末，复数渐渐被大多数人接受，当时卡斯帕尔·韦塞尔提出复数可看作平面上的一点。数年后，高斯再提出此观点并大力推广，复数的研究开始高速发展。
复数定义及运算
表示法一
复数通常写为如下形式：
\[a+bi
\]
这里的a和b是实数，而\(i\)是虚数单位，它有着性质\(i^2=-1\)。实数\(a\)叫做复数的实部，而实数\(b\)叫做复数的虚部。
- 实数可以认为是虚部为零的复数，即实数\(a\)等价于\(a+0i\)。
- 实部为零而虚部不为零的复数，也被叫做纯虚数
表示法二
复数可定义为实数\(a,b\)组成的有序对\((a,b)\)。在复平面坐标系中，用横轴表示实部，用纵轴表示虚部，用类似实数平面坐标系坐标点形式表示\((a,b)\)
<画个坐标系>
运算
形式上将代数的结合律、交换律、分配律应用到复数上，再加上等式\(i^2=-1\)，就可以定义复数域上的加减乘除运算了。
- 加法 \((a+bi) + (c+di) = (a+c) + (b+d)i\)
\[\begin{align}
&\ \ \ \ (a+bi) + (c+di) \\
&= a + bi + c + di \\
&= a + c + bi + di \\
&= (a+c) + (bi+di) \\
&= (a+c) + (b+d)i \\
\end{align}
\]
- 减法 \((a+bi) - (c+di) = (a-c) + (b-d)i\)
\[\begin{align}
&\ \ \ \ (a+bi) - (c+di) \\
&= a + bi + ((-c) + (-di)) \\
&= a + bi + (-c) + (-di) \\
&= (a+(-c)) + (bi+(-di)) \\
&= (a-c) + (b-d)i \\
\end{align}
\]
- 乘法 \((a+bi) \times (c+di) =(ac-bd)+ (ad+bc)i\)
\[\begin{align}
&\ \ \ \ (a+bi) \times (c+di) \\
&= (a+bi) \times c + (a+bi) \times di \\
&= a \times c + bi \times c + a \times di + bi \times di \\
&= ac + bci + adi + bdi^2 \\
&= ac + bdi^2 + bci + adi \\
&= (ac+bdi^2) + (bci+adi) \\
&= (ac-bd) + (bc+ad)i
\end{align}
\]
- 除法 \(\frac{a+bi}{c+di}=\frac{ac+bd}{c^2+d^2} + \frac{bc-ad}{c^2+d^2}i\)
\[\begin{align}
&\ \ \ \ \frac{a+bi}{c+di} \\
&=\frac{(a+bi)(c-di)}{(c+di)(c-di)} \\
&=\frac{ac+bci-adi-bdi^2}{c^2-(di)^2} \\
&=\frac{(ac+bd)+(bc-ad)i}{c^2+d^2} \\
&=\frac{ac+bd}{c^2+d^2} + \frac{bc-ad}{c^2+d^2}i
\end{align}
\]
注：假定\(\circ\), \(\bullet\)是一个二元运算符
- 交换律 \(x \circ y = y \circ x\)
- 结合律 \((x \circ y ) \circ z = x \circ (y \circ z)\)
- 分配律
(1) \(\circ\)对\(\bullet\)满足左分配律 \(x \circ (y \bullet z） = (x \circ z) \bullet (y \circ z)\)
(2) \(\circ\)对\(\bullet\)满足右分配律 \((y \bullet z) \circ x = (y \circ x) \bullet (z \circ x)\)
矩阵表达式
复数 \( a+bi \leftrightarrow \begin{bmatrix} a & -b \\ b & a \end{bmatrix} \)，在复数乘法中用到。
\[\begin{align}
&\ \ \ \ (a+bi)\times(c+di) \\
&= \begin{bmatrix} c & -d \\ d & c \end{bmatrix} \begin{bmatrix} a \\ b \end{bmatrix} \\
&= \begin{bmatrix} ac-bd \\ ad+bc \end{bmatrix} \leftrightarrow (ac-bd) + (ad+bc)i
\end{align}
\]
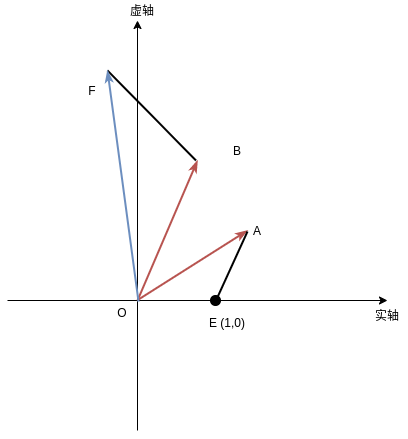
基于上面的表达式，复数域上乘以复数相当于，将复坐标系中坐标点围绕原点进行旋转。如下图所示，向量A与向量B的乘积向量F满足，三角形OEA与三角形OBF是相似的。
差异点
- 一般实数向量的乘法有标量乘法和矢量乘法，此处仅考虑标量乘法。即两个向量的乘法等于向量对应分量乘积之和。因此二维实数坐标系中点的乘法可表示为\((x_1, x_2) \cdot (y_1, y_2) = x_1y_1 + x_2y_2\)。用矩阵化形式表示为\((x_1, x_2) \begin{pmatrix} y_1\\y_2 \end{pmatrix} = x_1y_1 + x_2y_2\)
- 复数的乘法如\((a+bi)\times(c+di)\)按照实数加法和乘法的结合律、交换律和分配律，以及虚数定义\(i^2=-1\)可以得到\((a+bi)\times(c+di) = (ac-bd)+(bc+ad)i\)。
- 但是如果将复数用复平面上坐标点形式或者向量形式表示时，即复数\(a+bi\)用\((a,b)\)表示时，那么两个复数相乘，就表示复平面内两个复点向量相乘，其乘法结果并不如实数空间那样对应分量之积。具体形式如前面所述。之所以有这样区别是，复数乘法定义，而矩阵化形式是尤其推导而来的。注意这个先后顺序。
