强化学习 1
以下是对李宏毅老师 youtube视频-【机器学习2021】概述增强式学习一、二、三简要记录
https://www.youtube.com/watch?v=XWukX-ayIrs
https://www.youtube.com/watch?v=US8DFaAZcp4
https://www.youtube.com/watch?v=kk6DqWreLeU
什么是Reinforcement Learning(RL)?
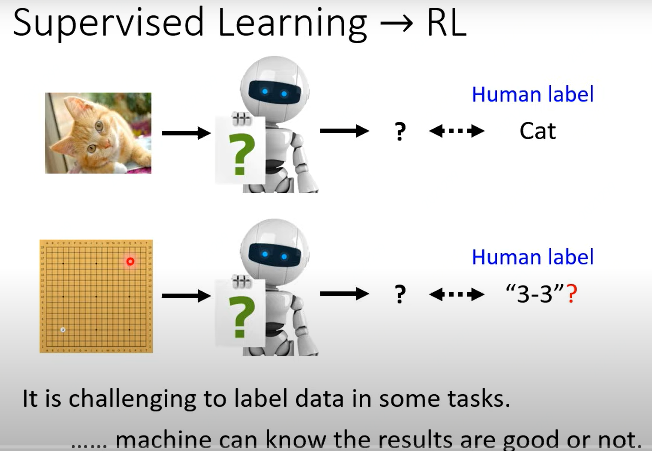
先回顾一下Supervised Learning,以图像分类任务为例,图像有标注的标签,如下图第一行所示。要训练的模型,输入Input是一张猫咪图片,输出Output是“Cat”。有十分明确的输出信息。(这里需要提到Autoencoder任务,实际上该类任务的输出与输入是一样,其实也是一种SP任务,只不过该类任务不需要标注数据而已。)
如下图第二行所示。以下围棋为例,输入一张当前围棋局,即使对于人来说,下一步该怎么走是对的或者是最好的,这些都不确定。 当遇到类似问题,可以考虑使用强化学习,其特点是很难标注数据或者获得正确的标签,但是执行某个操作后,机器是知道结果是好的或者坏的。
RL构成
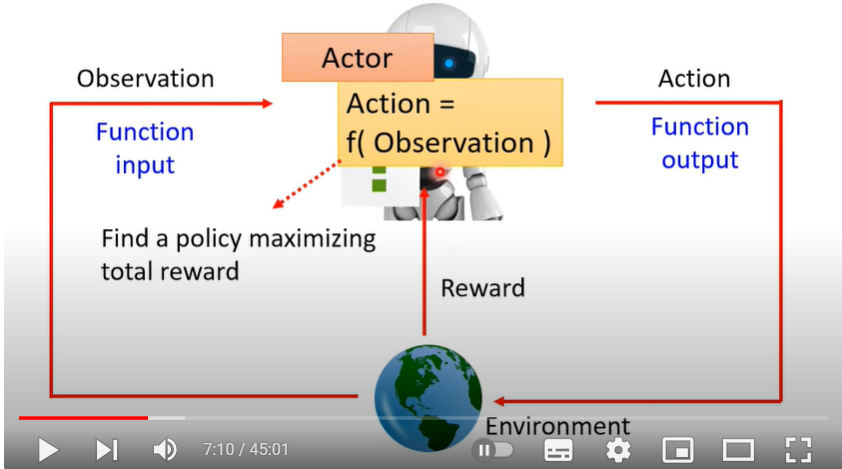
RL系统:2个对象与3种行动,如下图所示。
- 2个对象:Actor, Environment
- 3种行动:Actor进行观察Observation, Actor采取行动 Action;Environment进行奖励或惩罚Reward。
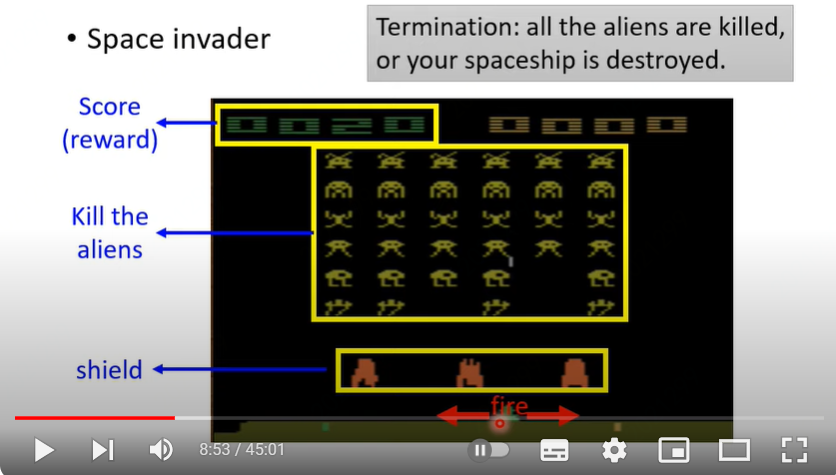
以太空入侵者游戏为例,Actor就是玩家,观察Obversation就是观看当前游戏界面,行动Action就是左移右移或者开火;Environment就是游戏机,游戏机的奖励就是界面左上角显示的分数。游戏结束条件:所有外星人都被杀死或者我方宇宙飞船被摧毁。
注:以太空入侵者为例,Actor每一步行动都会有明确的reward;而如下围棋游戏,并不是每一步都有reward,只有到游戏结束后才能知道最终的reward输或赢。
RL三步走
ML问题都可以通过以下三个步骤来完成
- Step1: function with unknown
- Step2: define loss from training data
- Step3: optimization
同样的,RL也可以分解为这三个步骤。
定义函数
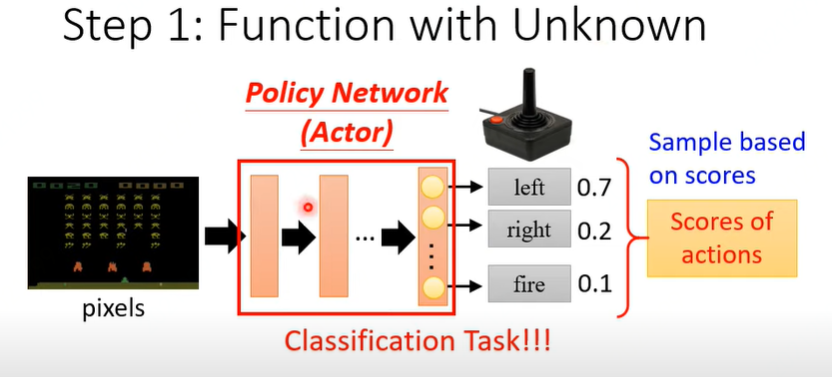
以太空入侵游戏为例,最简单的一种方式,可以将要建模的任务看做是一个分类任务。输入一帧当前游戏画面,训练一个CNN网络,网络输出左移、右移、开火三种动作的概率值。
定义损失
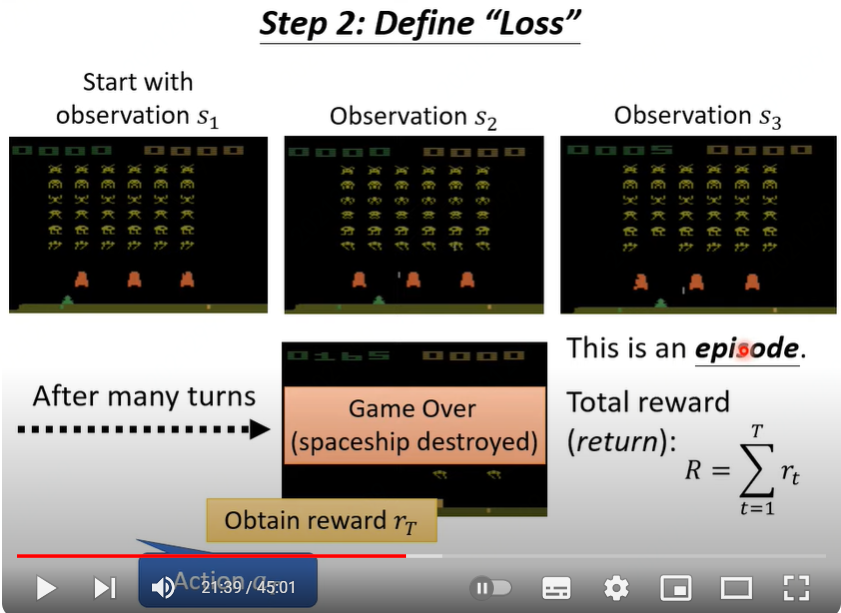
从游戏开始到游戏结束,称之为一个episode,整个过程中所有的奖励之和 \(R =\sum_{t=1}^{T} r_t\),将负的total reward作为RL损失
优化
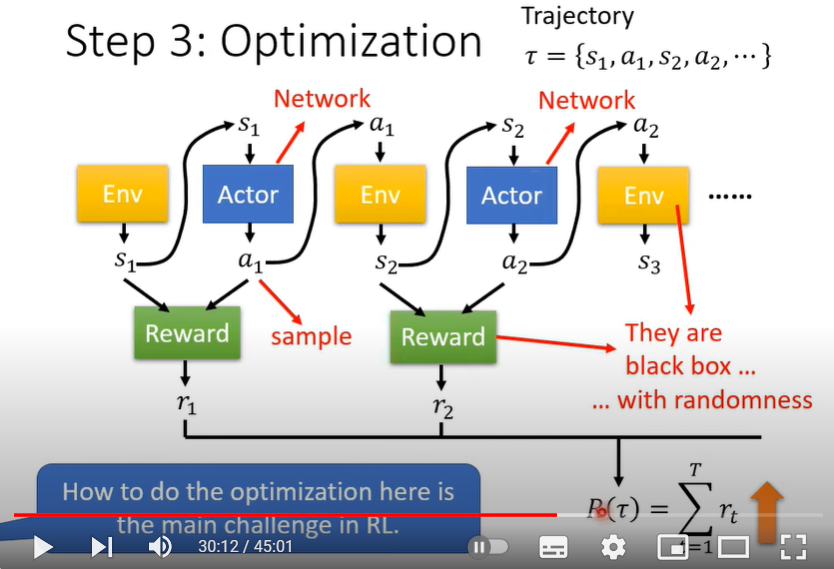
Actor依次观察到的状态\(s\)和接下来采取的行动\(a\),依次记为\(s_1, a_1, s_2, a_2, \cdots\),在一个episode中,这些有序的状态和行动构成序列\(\{s_1, a_1, s_2, a_2, \cdots\}\),用字母 \(\tau\)来表示,即\(\tau = \{s_1, a_1, s_2, a_2, \cdots\}\).
在一个episode过程中,要求总reward之和最大。优化的困难点在于
- Actor采取的action有随机性,即使是完全相同的输入
- Environment与Reward计算都是黑盒,也可能具有随机性
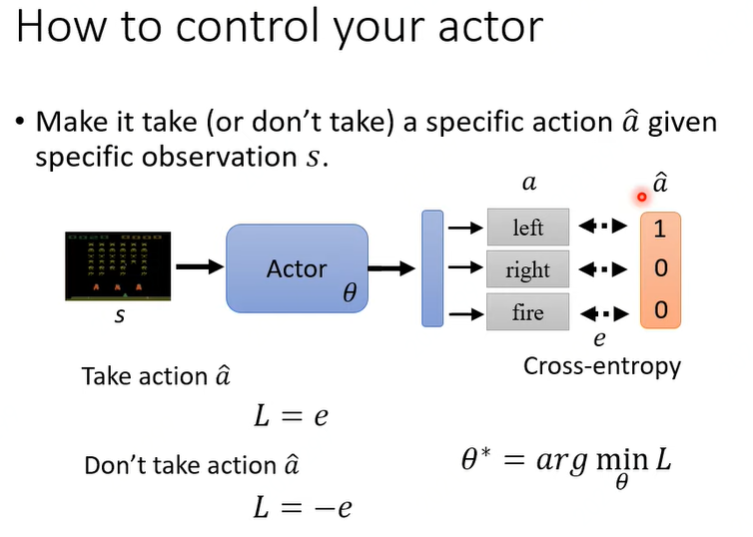
如何控制Actor的行动
仍以太空入侵游戏来说明,如果要采取某个行动,则让对应类别概率满足交叉熵最小,反之则要最大。如下图所示。
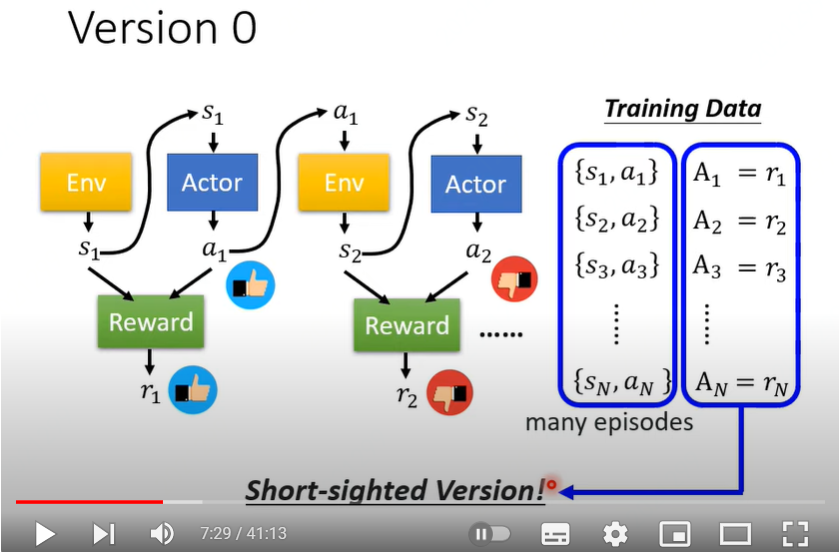
数据是如何收集
Version 0:
执行的$a_t $对应的那步reward值 \(r_t\) 作为\(A_t\)。但是这种方法很短视没有考虑长远影响,比如太空入侵游戏,虽然当前的左移或者右移没有杀死外星人,但是间接带来后续行动杀死了外星人。
注:强化学习任务往往具有下述特点:
- 一个action 影响了接下来的observation 和接下来的reward
- 奖励延迟:Actor必须牺牲当前的reward来获取更多的长期reward
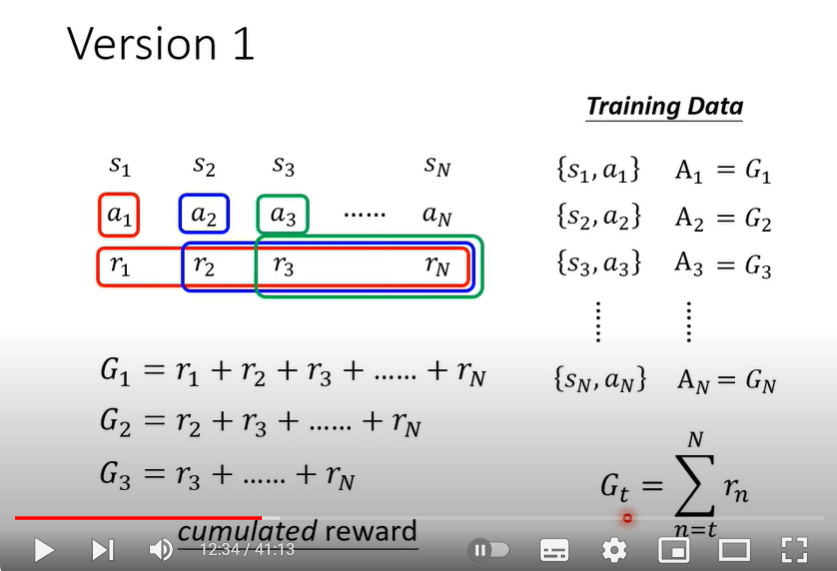
Version 1:
针对Version 0的问题进行优化,将Actor 第\(t\)步行动 \(a_t\) 当前及后续所有行动的reward之和作为\(A_t\). 即$$A_t = \sum_{n=t}^T r_n$$
Version 2:
Version 0,Version 1可以看出两种极端。一种是当前action仅影响当前reward,一种是当前action对后续所有action产生的reward也都要归功于当前action。Version 2就是不左不右。给予越远的action产生的reward赋予越小的累加和系数,即$$A_t = \sum_{n=t}^T \gamma^{n-t} r_n$$

Version 3:
之前的Version0-2 还存在一个问题,就是reward没有进行归一化或者标准化。

Policy Gradient
- 构建Actor网络参数并初始化参数为\(\theta^{0}\)
- 迭代训练 \(i={1,2,\cdots,T}\)
- 使用actor在参数取值为\(\theta^{i-1}\)时去与environment进行交互
- 获得交互数据 \({s_1,a_1, s_2, a_2, \cdots, s_N, a_N}\)
- 计算每步reward值\(A_1, A_2, \cdots, A_N\)
- 计算损失值\(L\)
- 更新参数 \(\theta^i \leftarrow \theta^{i-1} - \eta \Delta L\)
注:数据收集在循环内 \({s_1,a_1, s_2, a_2, …, s_N, a_N}\)是在 \(\theta^ {i-1}\) 下收集的。这种参数下,\(a_1, a_2, \cdots, a_N\) 产生的reward可以用于更新 \(\theta^ {i-1}\)。当进行到\(\theta^i\),上次收集的\({s_1,a_1, s_2, a_2, …, s_N, a_N}\)都不适合了,即使是相同的状态s,actor采取的action也可能不同。所以要重新收集。 也正是如此,policy gradient 很耗时。
On-Policy/Off-Policy
- On-policy: The actor to train and the actor for interacting is the same
- Off-policy: The actor to train and the actor for interacting is different
Off-policy方法就是为了解决上述问题,使得\(\theta^{ i-1}\) 条件下收集到的数据也可以用于更新\(\theta^{i}\),从而缓解每一次迭代都要重新收集数据问题。
PPO 视频链接: https://www.youtube.com/watch?v=OAKAZhFmYoI
Critic
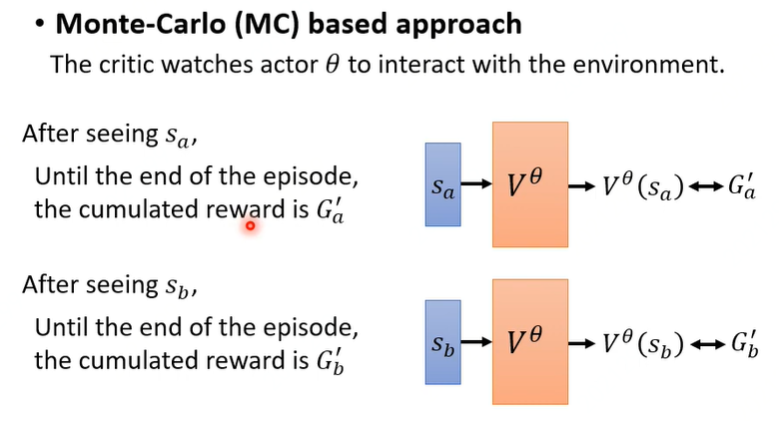
Value function \(V^{\theta}(s)\) : 在actor 参数为\(\theta\)时,当观察到environment的状态s,打折扣的累积reward。这个function的目的是预测,不必等玩完整个游戏才能获得。
\(V^{\theta}(s)\) 含义: 在观察到状态\(s_t\), 后续采取的action及reward,有多种可能,对应所有可能的最终reward求期望值,这个就是\(V^{\theta}(s)\) 。
如何估计\(V^{\theta}(s)\)
基于MC方法
直接观察,但要游戏玩到结束
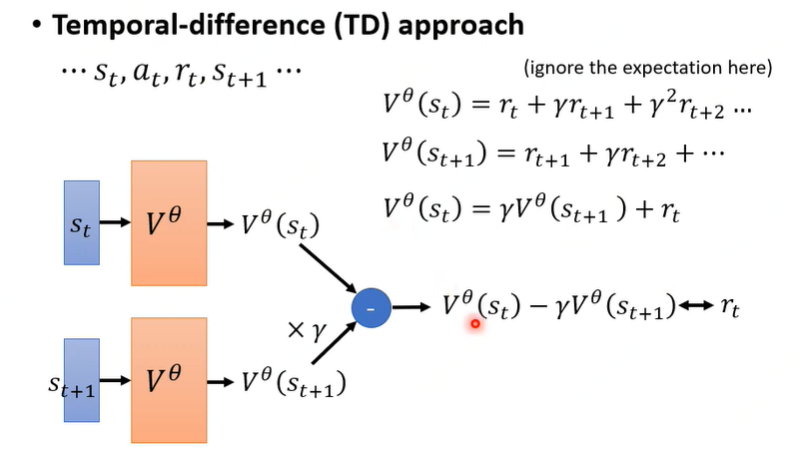
基于Temporal-difference TD 方法
不需要玩完整个游戏,仅仅知道\(s_t, a_t, r_t, s_{t+1}\) 就可以更新参数
使用打折扣的累积reward作为当前action的奖励,因此有
由上面两个公式,可以得到相邻两次行动\(a_t, a_{t+1}\)的产生的reward之间关系式,即
做一道作业
如下图所示,分别进行了8轮游戏。 观察到\(s_b\)采取行动后有6次reward为1,有2次reward为0,因此期望是\(\frac{3}{4}\),即\(V^{\theta}(s_b)=\frac{3}{4}\)。那么\(V^{\theta}(s_b)\)应该是多少呢?
- 基于MC
因为就观察到一次\(s_a\),且对于reward为0. 因此\(V^{\theta}(s_a)=0\) - 基于TD
由于只有第1个episode同时出现了\(s_a, s_b\), 而且\(V^{\theta}(s_a) = V^{\theta}(s_b) + r\),此时\(r=0\),因此\(V^{\theta}(s_a)=\frac{3}{4}\)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号