期望最大化EM算法(2)

一般形式的EM算法

  期望最大化算法或者EM算法是，求解具有潜在变量的概率模型的最大似然解的一种通用方法。这里给出一般形式的EM算法，并启发式地推导EM算法最大化了似然函数。

  考虑一个概率模型，将其中所有的观测变量联合起来记为\(X\), 将所有的与观测变量对应的潜在变量记为\(Z\)。联合概率分布\(p(X,Z|\theta)\)由一组参数控制，记为\(\theta\)。我们的目标是最大化似然函数

\[p(X|\theta) = \sum_{Z}p(X,Z|\theta) \tag{9.69} \]

  假设： 直接最优化\(p(X|\theta)\)比较困难，但是最优化完整数据似然函数 \(p(X,Z|\theta)\)就比较容易。

接下来，引入一个定义在潜在变量上的分布\(q(Z)\)，于是对于任意的\(q(Z)\)，下面的分解成立^[注1]。

\[log\ p(X|\theta) = L(q,\theta) + KL(q||p) \tag{9.70} \]

其中,

\[L(q,\theta) = \sum_{Z} q(Z) log \ \{ \frac{p(X,Z|\theta)}{q(Z)} \} \tag{9.71} \]

\[KL(q||p) = \sum_Z q(Z) log \ \{ \frac {q(Z)}{p(Z|X,\theta)} \} \tag{9.72} \]

注意：\(L(q,\theta)\) 是概率分布\(q(Z)\) 的一个泛函，也是参数参数 \(\theta\)的一个函数。

  由于KL散度始终大于等于0，因此\(L(q,\theta)\)是\(log \ p(X|\theta)\)的一个下界。 关于对数似然函数、下界和KL散度的三者关系如图9.11所示。

Fig. 9.11

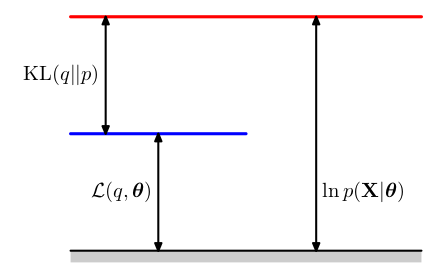
  下面是想通过最大化下界\(L(q,\theta)\)来最大化\(log \ p(X|\theta)\)。

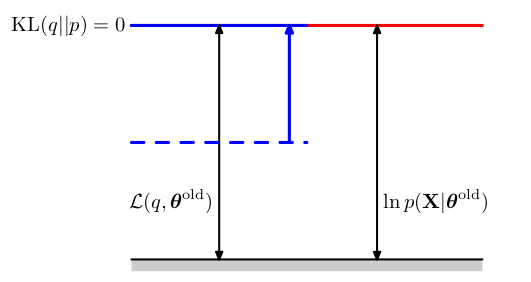
  在EM算法中E步骤中，在参数\(\theta^{old}\)固定情况下，关于分布\(q(Z)\)最大化下界\(L(q,\theta^{old})\)。由于\(log \ p(X|\theta)\)不依赖\(q(Z)\)，因此\(L(q,\theta^{old})\)的最大值出现在KL散度等于零的时候，即最大值出现在\(q(Z)\)与后验概率分布\(p(Z|X,\theta^{old})\)相等的时候。此时下界等于最大似然函数，如图9.12所示。

Fig. 9.12 当$q(Z)$设置为在当前参数$\theta^{old}$下的后验概率分布时，此时KL散度为0，似然函数的下界上移到与其值相同的位置。

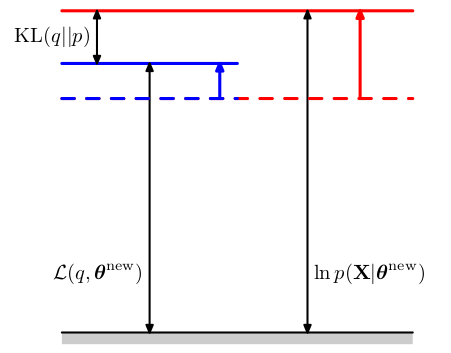
  在EM算法的M步骤中，分布\(q(Z)\)保持固定，下界\(L(q,\theta)\)关于\(\theta\)最大化，得到了某个新的值\(\theta^{new}\)，这会是的下界增大（除非已经达到了极大值）。由于在此过程中，分布\(q(Z)\)固定不变且是由旧的参数值\(\theta^{old}\)确定(\(q(Z)=p(Z|X,\theta^{old})\))，它不会等于新的后验概率分布\(p(Z|X,\theta^{new})\)，从而KL散度非零。于是对数似然函数的增加量就等于下界的增加量加上KL散度(非零)，因此对数似然函数的增加量大于下界的增加量。如图9.13所示。

Fig. 9.13

  将\(q(Z) = p(Z|X,\theta^{old})\)代入(9.71)，可以看到E步骤之后，下界的形式为

\[L(q,\theta) = \sum_Z p(Z|X,\theta^{old}) log \ p(X,Z|\theta) - \sum_Z p(Z|X,\theta^{old}) log \ p(Z|X,\theta^{old}) = \mathcal{Q}(\theta, \theta^{old}) + 常数 \]

从而在M步骤中，最大化的量时完整数据对数似然函数的期望，优化变量\(\theta\)只出现在对数运算内部。如果联合概率分布\(p(X,Z|\theta)\)是由指数形式，那么对数运算会抵消指数运算，从而使得M步骤最大化要比最大化不完整数据对数似然函数\(p(X|\theta)\)要容易很多。

注1： 公式(9.70)是如何推导的呢？
  为方便理解，下面推导省略 \(\theta\)，并以连续变量形式进行，离散形式同理。\(p(X) = \frac{p(X,Z)}{p(Z|X)}\)，因为要引入关于潜在变量\(Z\)的概率分布\(q(Z)\)，因此自然想到

\[p(X) = \frac{p(X,Z)}{p(Z|X)} = \frac{p(X,Z)}{q(Z)} \cdot \frac{q(Z)}{p(Z|X)} \]

两边同时取对数得到

\[log \ p(X) = log \ \frac{p(X,Z)}{q(Z)} + log \ \frac{q(Z)}{p(Z|X)} \]

观察公式(9.71)和(9.72)，对数前面都乘以了\(q(Z)\)，这里就要用到概率分布关于对应变量求积分或求和等于1的特性。于是对上述公式两边同时乘以\(q(Z)\)再取关于变量\(Z\) 的积分得

\[\int q(Z)log \ p(X) dZ = \int q(Z) log \ \frac{p(X,Z)}{q(Z)} dZ + \int q(Z) log \ \frac{q(Z)}{p(Z|X)} dZ \]

由于\(\int q(Z)log \ p(X) dZ\)中求积分是关于变量\(Z\)的，与\(log \ p(X)\)没有关系，可以写到积分号外面，因此\(\int q(Z)log \ p(X) dZ = log \ p(X) \int q(Z)dZ = log \ p(X)\)。因此对应公式(9.70)左侧，乘以\(q(Z)\)并取积分，并没有改变其值。最终得到

\[log \ p(X) = \int q(Z) log \ \frac{p(X,Z)}{q(Z)} dZ + \int q(Z) log \ \frac{q(Z)}{p(Z|X)} dZ \]

其中，

\[L(q,\theta) = \int q(Z) log \ \frac{p(X,Z)}{q(Z)} dZ \]

\[KL(q||p) = \int q(Z) log \ \frac{q(Z)}{p(Z|X)} dZ \]

使用离散写法就是上述公式(9.70)和(9.71)。更详细地推导方式可以参考《VAE变分自编码器公式推导》https://www.cnblogs.com/wolfling/p/16452537.html