K-均值
K均值聚类
我们现在考虑这个问题：寻找多维空间中数据点的分组或者聚类问题。假设有一个数据集 \({x_1, x_2, ... x_N}\)，它是D维欧几里得空间中的随机变量 \(\pmb x\)的N次观测组成的。我们的目标是将数据集划分为K个类别。先假定K的值是给定的。
直观上讲，我们认为一组数据点中的一个聚类中，内部点之间的距离应该小于该聚类中数据点与外部点之间的距离。不妨设这个聚类为区域\(R_1\)中有M个数据点 \({x_{s_1}, x_{s_2}, x_{s_M}}\)，其中 \({s_1, s_2, ..., s_N}\) 是数字 \({1, 2, ..., N}\) 的一个排列。那么直白地翻译上述为 $$\underset{i<j,i,j=1,2,...,M} {max} |x_{s_i} - x_{s_j}|< \underset{i=1,2,...,M, j=M+1,...,N} {min}|x_{s_i} - x_{s_j}|$$ 可以看出这种形式化的表示比较繁琐。
现在引入一组D维向量 \(\mu_k, k=1,2,...,K\)是K个聚类的代表，认为是对应聚类的中心。那么我们的目标就是找到一组向量 \({\mu_k}\) 及数据点所属的聚类，使得每个数据点和它最近的向量 \(\mu_k\)之间的距离是最小的，即 \(|x_n - \mu_k|\) 是所有选择中最小的。
为了方便构建目标函数，引入了二值指示变量 \({r_{nk}} \in \{0,1\}, k=1,2,...,K\)对应同一个数据点，这n个值只有一个等于1，其余都等于0。如果 \(r_{nk}=1\)即数据点属于聚类k，这种表示方式称之为"1 of K"。为此我们可以定义一个目标函数：
这个公式涉及到两种量，聚类中心 \(\{\mu_k\}\) 和 分配\(\{r_{nk}\}\), 分配会随着聚类中心发生变化。可以使用一种迭代的方法求解使得目标函数最小。
第一阶段是固定 \(\{\mu_k\}\) ，关于 \(\{r_{nk}\}\) 最小化\(J\)；第二阶段是固定 \(\{r_{nk}\}\) 关于 \(\{\mu_k\}\) 最小化\(J\)。
第一阶段是固定 \(\{\mu_k\}\) ，关于 \(\{r_{nk}\}\) 最小化\(J\)。由于不同n相关的项是相互独立的，因此可以对于每个n分别进行最优化，只要k的值使得 \(||x_n-\mu_k||^2\) 最小,我们就令 \(r_{nk} = 1\),即
第二阶段是固定 \(\{r_{nk}\}\) 关于 \(\{\mu_k\}\) 最小化\(J\)。目标函数是 \(\mu_k\)的一个二次函数，令它关于\(\mu_k\)的导数等于零，即可达到最小值，即
可以很容易求得
这个公式中分母表示聚类k中数据点的数量，分母是聚类k中数据点之和，合在一起就是聚类k中所有数据点的均值。因此求得的聚类k的聚类中心就等于属于这个聚类的数据点的均值。这就是K均值算法（K-means）的由来。为数据点分配聚类的步骤和计算聚类中心的步骤不停迭代进行，直到聚类的分配不再改变或者直到达到一定的迭代次数停止。由于每个阶段都减小了目标函数的值，因此算法的收敛性得到保证。
下面以随机数和老忠实间歇喷泉为例，来编程实现K-means代码。
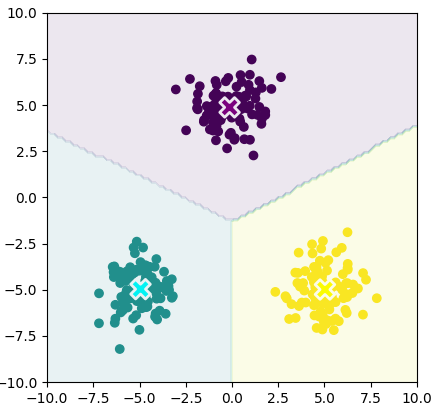
示例1
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import fetch_openml
from prml.clustering import KMeans
from prml.rv import (
MultivariateGaussianMixture,
BernoulliMixture
)
# training data
x1 = np.random.normal(size=(100, 2))
x1 += np.array([-5, -5])
x2 = np.random.normal(size=(100, 2))
x2 += np.array([5, -5])
x3 = np.random.normal(size=(100, 2))
x3 += np.array([0, 5])
x_train = np.vstack((x1, x2, x3))
x0, x1 = np.meshgrid(np.linspace(-10, 10, 100), np.linspace(-10, 10, 100))
x = np.array([x0, x1]).reshape(2, -1).T
kmeans = KMeans(n_clusters=3)
kmeans.fit(x_train)
cluster = kmeans.predict(x_train)
plt.scatter(x_train[:, 0], x_train[:, 1], c=cluster)
plt.scatter(kmeans.centers[:, 0], kmeans.centers[:, 1], s=200, marker='X', lw=2, c=['purple', 'cyan', 'yellow'], edgecolor="white")
plt.contourf(x0, x1, kmeans.predict(x).reshape(100, 100), alpha=0.1)
plt.xlim(-10, 10)
plt.ylim(-10, 10)
plt.gca().set_aspect('equal', adjustable='box')
plt.show()
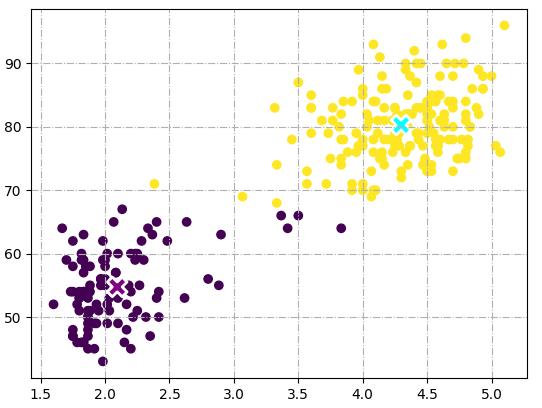
示例2
import pandas as pd
csv_data = pd.read_csv('data.csv')
x_train = csv_data.to_numpy()
kmeans = KMeans(n_clusters=2)
kmeans.fit(x_train)
cluster = kmeans.predict(x_train)
plt.scatter(x_train[:, 0], x_train[:, 1], c=cluster)
plt.scatter(kmeans.centers[:, 0], kmeans.centers[:, 1], s=200, marker='X', lw=2, c=['purple', 'cyan'], edgecolor="white")
plt.grid(linestyle='-.')
plt.show()
【参考】
1.Pattern Recognition and Machine Learing 中/英文版
2.https://github.com/ctgk/PRML
