机器学习——随机变量
在上学时代和工作期间,经常会遇到概率论中相关概念,这里再重新来认识一下随机变量相关概念。包括随机变量(离散随机变量、连续随机变量)、分布列、概率密度函数、分布函数等。下面都是来自茆诗孙版本《概率论与数理统计》
1. 随机变量的概念
1.1 随机变量的引入
在本书中,“用来表示随机现象结果的变量”称为随机变量。随机现象中有很多样本点本身就是用数量来表示的,由于样本点出现的随机性,其数量是随机的,也称为随机变量。也有样本点不是数,这时也可以根据研究设计出随机变量,可以用数量来表示。先看第一种情况,在实际生活中的例子。
- 投掷一个骰子,出现的点数X是一个随机变量
- 每天进入某个超市的顾客数量Y,顾客购买商品的件数U,顾客排队等候付款的时间V,是三个不同的随机变量
- 电视机的寿命T是一个随机变量
- 测量的误差\(\epsilon\) 是一个随机变量
- 检查工厂生产的产品是否合格,则其样本工具\(\Omega={合格品,不合格品}\),这时可以设计一个随机变量X如下:
| 样本点 | X的取值 |
|---|---|
| 合格品 | 0 |
| 不合格品 | 1 |
- 检查三个产品,则有8个样本点,如记X为“三个产品中的不合格品数”,则X与样本点之间有如下对应关系:
| 样本点 | X的取值 |
|---|---|
| \(\omega_0=(0,0,0)\) | 0 |
| \(\omega_0=(1,0,0)\) | 1 |
| \(\omega_0=(0,1,0)\) | 1 |
| \(\omega_0=(0,0,1)\) | 1 |
| \(\omega_0=(1,1,0)\) | 2 |
| \(\omega_0=(1,0,1)\) | 2 |
| \(\omega_0=(0,1,1)\) | 2 |
| \(\omega_0=(1,1,1)\) | 3 |
1.2 随机变量定义
定义 定义在样本空间\(\Omega\)上的实值函数\(X=X(\omega)\)称为随机变量,常用大写字母X,Y,Z等表示随机变量,其取值用小写字母x,y,z等表示。假如一个随机变量仅取有限个或可列个值,则称其为离散随机变量。假如一个随机变量的可能取值充满数轴上的一个区间(a,b),则称其为连续随机变量,其中a可以是\(-\infty\), b可以是\(+\infty\)。
这个定义表明:随机变量X是样本点\(\omega\)的一个函数,这个函数可以是不同样本点对应不同的实数,也可以是多个样本点对应同一个实数。这个函数的自变量(样本点)可以是数,也可以不是数,但是因变量(随机变量取值)一定是实数。正如前面所述,“用来表示随机现象结果的变量”,随机现象就是各种样本,这些样本的某种结果可以用一个变量来表示,这个变量就是随机变量。
对于随机变量,研究它不仅要知道它可以取那些值,还要知道这些值的概率是多少。
2.随机变量的分布函数
2.1 分布函数引入
随机变量X是样本点\(\omega\)的一个实值函数。若B是某些实数组成的集合,即\(B\in R\),R表示实数集,则\(X\subset B\)表示如下随机事件
\({\{\omega:X(\omega) \in B}\}\subset \Omega\)
这个就是我们可以用随机变量取某些值表示随机事件的依据。譬如
- 记X表示投掷一个骰子出现的点数,则X的可能取值为1,2,..., 6. 这是一个离散随机变量。事件A=“点数小于等于3”,可以表示为A=
- 记Y表示一天内到达某商场的顾客数,则Y的可能取值为0,1,2,..., n, ...这也是一个离散随机变量。事件B=“至少来1000位顾客”,可以表示为B=
- 记T表示某电器的使用寿命,则T的可能取值充满区间\({[0, +\infty)}\)。这是一个连续随机变量。事件C=“使用寿命在40000至50000小时之间”,可以表示为C=
为了掌握X的统计规律,我们只要掌握X取各种值得概率,这是由于\({ \{ a<X\leq b \}=\{X \leq b\}-\{x \leq a\} }\).因此只要对任意实数x,知道了事件\(X \geq x\)的概率就够了,这个概率具有累积特性,常有F表示。另外这个概率与x有关,不同的x,此累积概率值也不同,为此记为
\(F(x)=p(X \leq x)\)
于是F(x)对于任意\(x\in (-\infty, +\infty)\)都有定义,而F(x)是定义在\((-\infty, +\infty)\)上、取值于[0,1] 的一个函数。
2.2 分布函数
定义 设X是一个随机变量,对于任意的实数x,称
\(F(x)=p(X \leq x)\)
为随机变量X的分布函数。且称X服从F(x), 记为\(X \backsim p(X \leq x)\)。
定理 任意分布函数F(x)都具有下面三条基本性质:
(1)单调性 F(x)是定义在整个实数轴上的单调非减函数,即对于任意的\(x_1<x_2\),有\(F(x_1) \leq F(x_2)\)
(2)有界性 对于任意的x,有\(0 \leq F(x) \leq 1, F(-\infty)=\lim_{x \to - \infty}F(x)=0, F(+\infty)=\lim_{x \to + \infty}F(x)=1\)
(3)右连续性 F(x)是x的右连续函数,即对于任意的\(x_0\), 有$ \lim_{x \to x_0+}F(x)=F(x_0)$
3. 概率分布
离散随机变量的概率分布可以用概率分布列来表示,连续随机变量的概率分布可以用概率密度来表示。由于离散随机变量,可以认为形式上可以列举的,我们将离散随机变量取各个值得概率,用数列的方式列举出来。而连续随机变量却不行,只能用函数的形式来表示。
3.1 分布列
定义 设X是一个离散的随机变量,如果X的所有可能取值是\(x_1, x_2, ..., x_n, ...\)则称X取\(x_i\)的概率为
\(p_i=p(x_i)=P(X=x_i),i=1,2,...,n,...\)
为X的概率分布列或简称分布列,可以用下面列表方式来表示
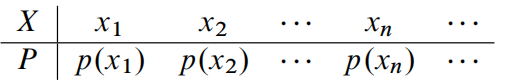
分布列的基本性质
(1)非负性:\(p(x_i) \geq 0, i=1,2,...\)
(2)正则性:\(\sum_{1}^{\infty}=1\)
3.2 概率密度函数
连续随机变量的一切可能取值是充满某个区间(a,b), 在这个区间内有无穷多个不可列实数,因此描述连续随机变量的概率分布不能再用分布列的形式表示,而是该用概率密度函数表示。下面用一个实例来引出概率密度函数。
例 新生婴儿的体重X是一个随机变量(常识也告诉我们这个是一个连续随机变量),假如记录有很多个(例如十万个)新生婴儿的体重,我们将各种体重的频率用直方图的形式表示出来,x轴表示体重(单位:500g),y轴表示单位长度上的频率。则以下图中的(a)至(c)表明,当\(\Delta =1\)越来越小,其频率直方图越来越光滑。
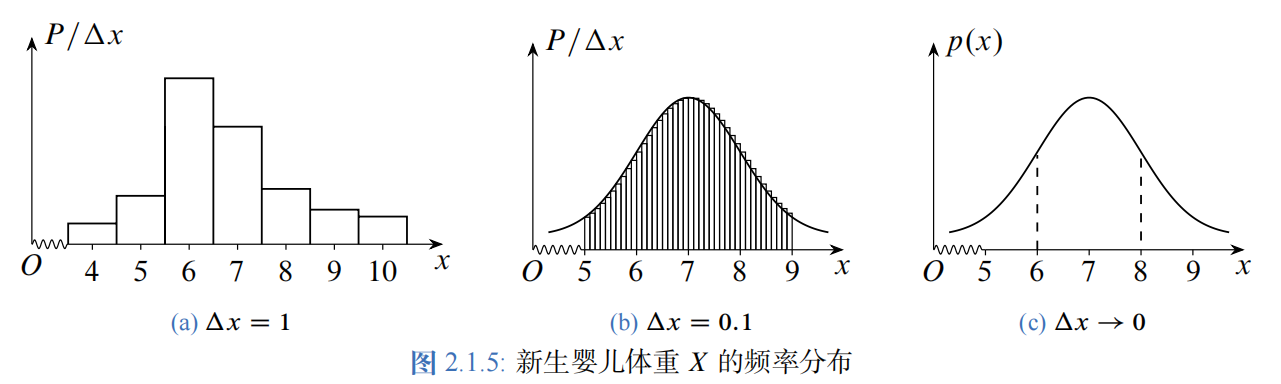
(1)当\(\Delta =1\),体重的频率直方图如(a)。图中矩形宽度为1,高度为频率,所有矩形面积之和为1.此时体重X的取值为1,2,...,即X是一个离散随机变量。
(2)当\(\Delta =0.1\),体重的频率直方图如(b)。图中矩形宽度为0.1,高度为频率/0.1,所有小矩形的面积之和仍为1.
(3)当\(\Delta \to 0\),则体重的频率图趋于图(c)所表示的一条光滑的曲线,其高度为频率密度值。如果记这条曲线为\(p(x)\),则\(p(x)\)与\(x\)轴所夹面积仍为1.此时体重X的取值充满某一区间,即X是一个连续随机变量。图中\(p(x)\)就是连续随机变量X的概率密度函数。
定义 设随机变量X的分布函数为F(x),如果存在一个实数轴上一个非负可积函数p(x),使得对任意实数x有
\(F(x)=\int_{-\infty}^{x} p(t)dt\)
可以看出,在F(x)导数存在的点上有
\(F^{'}(x)=p(x)\)
F(x)是累积概率函数,其导数p(x)是概率密度函数。
密度函数的基本性质
(1)非负性: \(p(x) \geq 0\)
(2)正则性: \(\int_{-\infty}^{+\infty}p(x)dx=1\)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号